
- •1. Построение интервального вариационного ряда распределения
- •2. Вычисление выборочных характеристик распределения (непосредственно)
- •Метод произведений вычисления выборочных средней и дисперсии
- •3 Графическое изображение вариационных рядов.
- •4. Расчет теоретической нормальной кривой распределения.
- •5. Проверка гипотезы о нормальном законе распределения
Метод произведений вычисления выборочных средней и дисперсии
Если
выборка задана в виде равностоящих
вариант и соответствующих им частот,
тот удобно находить выборочную среднюю
и дисперсию методом произведений по
формулам
![]() ,
,![]() ,
гдеh-шаг
(разность между двумя соседними
вариантами), С—ложный нуль (варианта,
которая расположена примерно в середине
вариационного ряда);
,
гдеh-шаг
(разность между двумя соседними
вариантами), С—ложный нуль (варианта,
которая расположена примерно в середине
вариационного ряда);
![]() --условная
варианта;
--условная
варианта;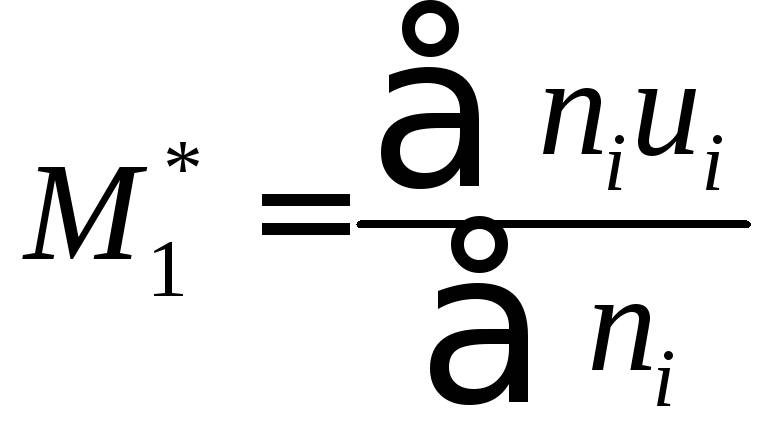 -условный
момент первого порядка,
-условный
момент первого порядка,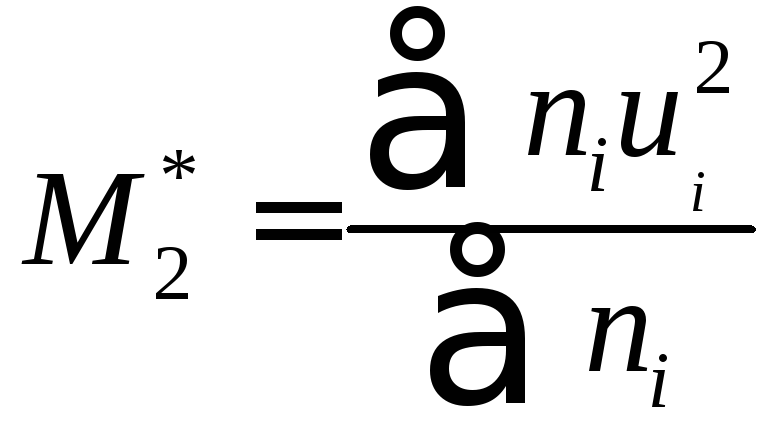 -условный
момент второго порядка.
-условный
момент второго порядка.
Если первоначальные варианты не являются равностоящими, то интервал, в котором заключены все варианты выборки, делят на несколько равных, длины h, частичных интервалов (каждый частичный интервал должен содержать не менее 8-10 вариант). Затем находят середины частичных интервалов, которые образуют последовательность равностоящих вариант. В качестве частоты каждой середины интервала принимают сумму частот вариант, которые попали в соответствующий частичный интервал.
При вычислении выборочной дисперсии для уменьшения ошибки, вызванной группировкой (особенно при малом числе интервалов), делают поправку Шеппарда, а именно вычитают 1/12 квадрата длины частичного интервала. Таким образом с учетом поправки Шеппарда дисперсию вычисляют по формуле
![]() .
.
Возьмем шаг h=0,205. Отрезок [5.03,5.85] разобьем на 4 интервала.
|
|
|
|
|
|
|
|
|
[5.03,5.24] |
5.14 |
10 |
-2 |
-20 |
40 |
10 |
|
[5.24,5.44] |
5.34 |
41 |
-1 |
-41 |
41 |
0 |
|
[5.44,5.65] |
5.55=C |
39 |
0 |
A1=-61 |
0 |
39 |
|
[5.65,5.85] |
5.75 |
10 |
1 |
10 |
10 |
40 |
|
|
|
|
|
A2=10 |
|
|
|
сумма |
|
100 |
|
-51 |
91 |
89 |
Для контроля вычислений пользуются тождеством

Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого и второго порядков.

![]()
![]()
Метод сумм вычисления выборочных средней и дисперсии
При
использовании метода сумм условные
моменты первого и второго порядков
находят по формулам:
![]() ,
,![]() ,
где
,
где![]() .
Таким образом, в конечном счете, надо
вычислить числа
.
Таким образом, в конечном счете, надо
вычислить числа![]()
|
|
|
|
|
|
5.14 |
10 |
10 |
10 |
|
5.34 |
41 |
51 |
0 |
|
5.55=C |
39 |
0 |
0 |
|
5.75 |
10 |
10 |
0 |
|
|
100 |
|
|

![]()
![]()
![]()
![]()
Асимметрия
и эксцесс эмпирического распределения.
![]() .
.![]() .
.![]() ,
,![]() -центральный
эмпирические моменты третьего и
четвертого порядка.
-центральный
эмпирические моменты третьего и
четвертого порядка.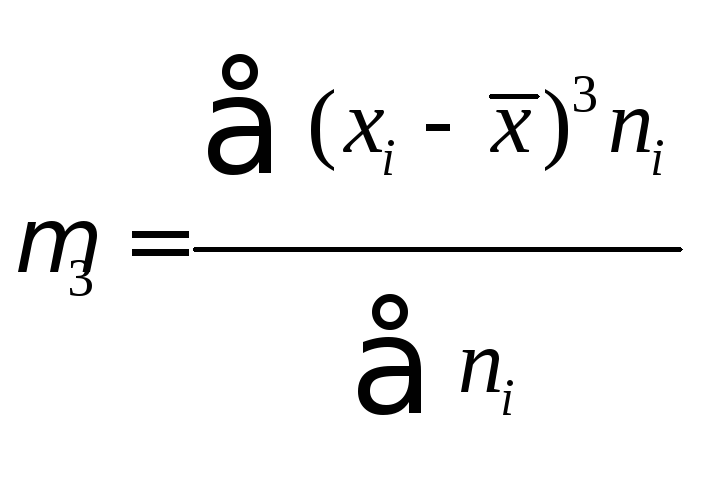
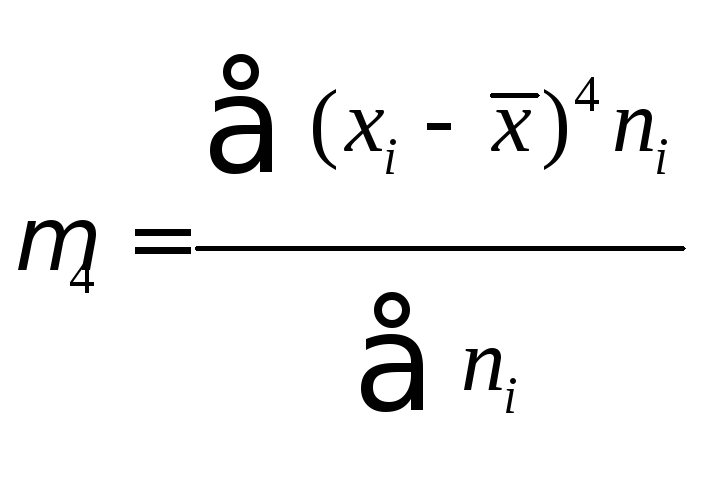 .Эти
моменты в случае равностоящих вариант
с шагомh
(шаг равен разности между двумя соседними
вариантами) удобно вычислять по формулам:
.Эти
моменты в случае равностоящих вариант
с шагомh
(шаг равен разности между двумя соседними
вариантами) удобно вычислять по формулам:
![]()
![]() ,
где
,
где
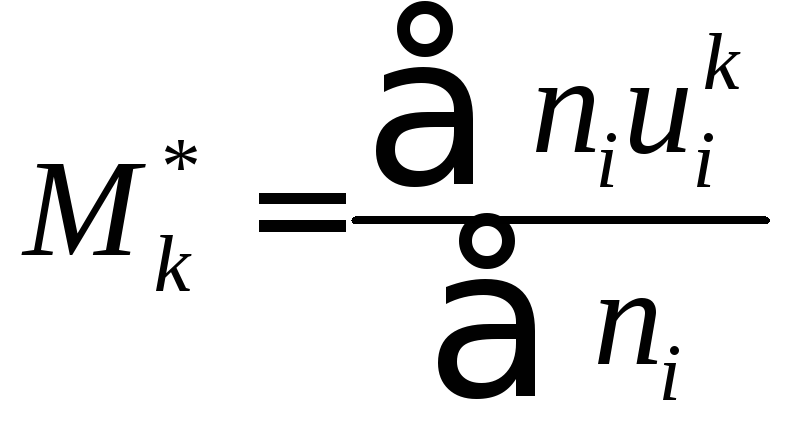 -условный моментk-ого
порядка,
-условный моментk-ого
порядка,
![]() -условная
варианта. Итак, для отыскания асимметрии
и эксцесса необходимо найти условные
моменты, что можно сделать методом сумм
или методом произведений.
-условная
варианта. Итак, для отыскания асимметрии
и эксцесса необходимо найти условные
моменты, что можно сделать методом сумм
или методом произведений.
|
|
|
|
|
|
|
|
|
|
|
[5.03,5.24] |
5.14 |
10 |
-2 |
-20 |
40 |
-80 |
160 |
10 |
|
[5.24,5.44] |
5.34 |
41 |
-1 |
-41 |
41 |
-41 |
41 |
0 |
|
[5.44,5.65] |
5.55=C |
39 |
0 |
A1=-61 |
0 |
-121 |
0 |
39 |
|
[5.65,5.85] |
5.75 |
10 |
1 |
10 |
10 |
10 |
10 |
160 |
|
|
|
|
|
A2=10 |
|
10 |
|
|
|
сумма |
|
100 |
|
-51 |
91 |
-111 |
211 |
209 |
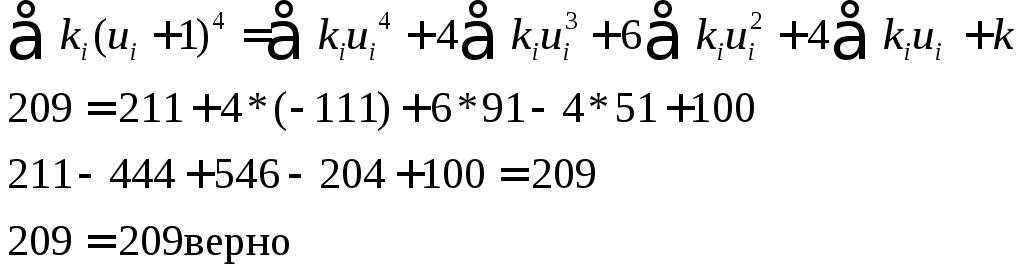
![]()
![]()
![]()

![]()
![]()
Или
|
|
|
|
|
|
|
|
5.14 |
10 |
10 |
10 |
0 |
0 |
|
5.34 |
41 |
51 |
0 |
0 |
0 |
|
5.55=C |
39 |
0 |
0 |
0 |
0 |
|
5.75 |
10 |
10 |
0 |
0 |
0 |
|
|
100 |
|
|
|
|
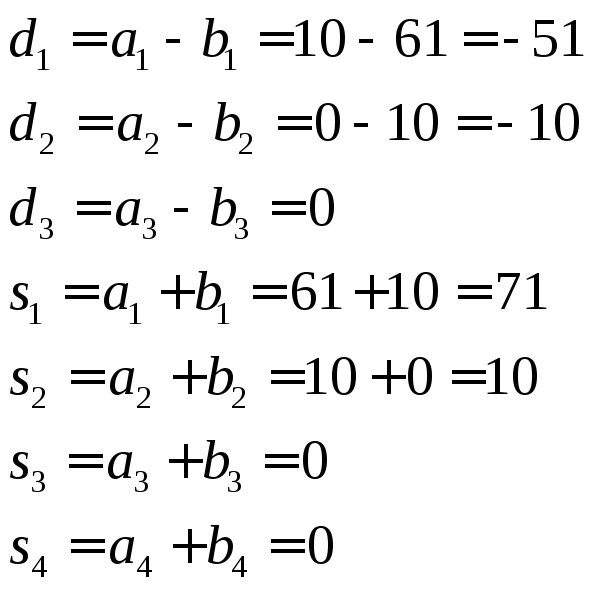
![]()
![]()
![]()
![]()
![]()
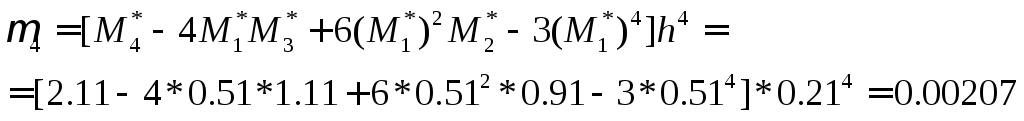
Медиана
![]() -значение
признака
-значение
признака![]() ,
приходящееся на середину ранжированного
ряда наблюдений (n=2l-1).
При четном числе наблюдений (n=2l)
медианой
,
приходящееся на середину ранжированного
ряда наблюдений (n=2l-1).
При четном числе наблюдений (n=2l)
медианой
![]() является средняя арифметическая двух
значений, расположенных в середине
ранжированного ряда:
является средняя арифметическая двух
значений, расположенных в середине
ранжированного ряда: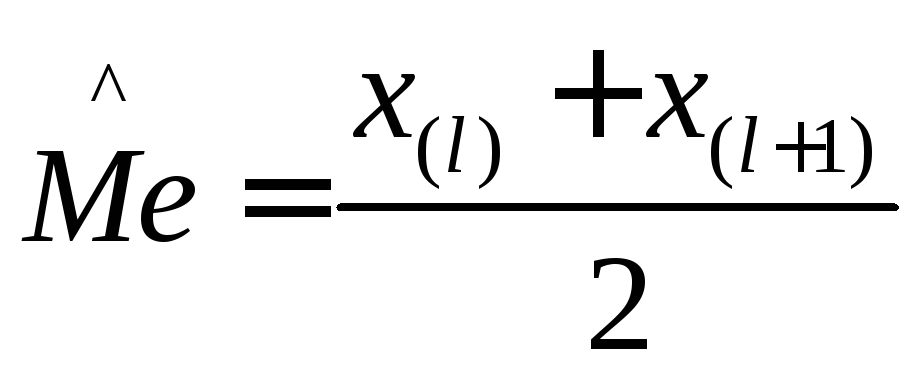 .
.
Если ранжировать
значения, попавшие в медианный интервал
[5,41;5,52], интервал, в котором накопленная
частота
![]() впервые превышает половину объема
выборки
впервые превышает половину объема
выборки![]() ,
-до значений
,
-до значений![]() и
и![]() ,
получим
,
получим![]()
Следовательно,
![]()
Если исходить из интервального ряда, то медиану следует вычислять по формуле
 ,
где
,
где
![]() означает номер медианного интервала,
означает номер медианного интервала,![]() -интервала,
предшествующего медианному.
-интервала,
предшествующего медианному.
В нашем примере
![]() млн.руб.
млн.руб.
Мода
![]() для совокупности наблюдений равна тому
значению признака (табл.1.1.), которому
соответствует наибольшая частота. У
нас вариант 5,43 имеет наибольшую частоту
(
для совокупности наблюдений равна тому
значению признака (табл.1.1.), которому
соответствует наибольшая частота. У
нас вариант 5,43 имеет наибольшую частоту
(![]() ).
Это означает, что
).
Это означает, что![]() млн.руб.Для одномерного интервального
ряда вычисление моды можно производить
по формуле:
млн.руб.Для одномерного интервального
ряда вычисление моды можно производить
по формуле:
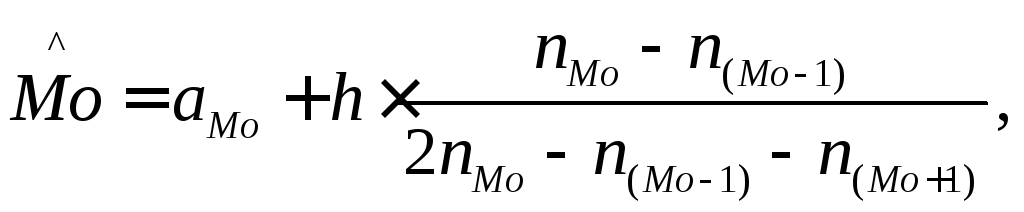 где
Мо означает
номер модального интервала (интервала
с наибольшей частотой),
где
Мо означает
номер модального интервала (интервала
с наибольшей частотой),
![]() и
и![]() -
номера соответствующего модальному и
следующего за ним интервалов.
-
номера соответствующего модальному и
следующего за ним интервалов.
В нашем примере
![]() млн.
руб. Так как
млн.
руб. Так как
![]() почти не отличаются друг от друга, есть
основания предполагать теоретическое
распределение нормальным.
почти не отличаются друг от друга, есть
основания предполагать теоретическое
распределение нормальным.
Коэффициент
вариации
![]()
