Энергетические характеристики сигналов

Основными энергетическими характеристиками сигнала s(t) являются егомощностьиэнергия.

Мгновенная мощность p(t) для вещественного сигнала определяется как

а для комплексного как

где знак " * " означает комплексно сопряженную функцию.

Если s(t) - напряжение или ток, тоp(t) есть мгновенная мощность, выделяемая на сопротивлении 1 Ом.

Энергия сигнала на интервале ( t₂ ,t₁ ) определяется как интеграл от мгновенной мощности

Отношение

имеет смысл средней на интервале ( t₂ ,t₁ ) мощности.

Для неограниченных по времени периодических сигналов определяют среднюю за период мощность

Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение

u(t), v(t) =u(t)v(t) dt = 0.

Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен  = 90^о), полностью независимыми друг от друга (некоррелированными, r = cos , и имеют нулевую энергию взаимодействия (E_uv = 0).

Рис. 2.3.1. Ортогональные сигналы.

На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевое скалярное произведение двух левых сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух правых - взаимным расположением (ненулевые значения сигналов не имеют общих координат).

Попутно заметим, что энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, нулевую энергию взаимодействия.

Норма сигналов в линейном пространстве является аналогом длины векторов, и обозначается индексом ||s(t)|| - норма (norm). В математике существуют различные формы норм. При анализе сигналов обычно используются квадратичные нормы

||s(t)|| =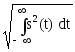. (2.1.2)

Для дискретных сигналов:

||s(n)|| =. (2.1.2')

Для комплексных сигналов

||s(t)|| =, (2.1.2'')

где s*(t) – величины, комплексно сопряженные с s(t).

Линейное пространство сигналов L является нормированным, если каждому сигналу пространства s(t) однозначно сопоставлена его числовая норма ||s(t)||, и выполняются следующие аксиомы:

1. Норма неотрицательна (||s(t)|| ≥ 0) и равна нулю тогда и только тогда, когда сигнал равен нулю (||s(t)|| = , при s(t) = ).

2. Для любого числа b должно быть справедливо равенство ||bs(t)|| = |b|  ||s(t)||.

3. Если v(t) и u(t) – сигналы из пространства L, то должно выполняться неравенство треугольника ||v(t)+u(t)||  ||v(t)|| + ||u(t)||.

Пример норм для двумерных цифровых сигналов приведен на рис. 2.1.2.

Энергетические спектры сигналов [1].

Скалярное произведение сигналов.Энергия суммы двух произвольных сигналов u(t) и v(t) определяется выражением

E =[u(t)+v(t)]² dt = E_u + E_v + 2u(t)v(t) dt. (7.2.1)

Как следует из этого выражения, энергии сигналов, в отличие от самих сигналов, в общем случае не обладают свойством аддитивности. Энергия суммарного сигнала u(t)+v(t), кроме суммы энергий составляющих сигналов, содержит в себе и так называемую энергию взаимодействия сигналов или взаимную энергию

E_uv= 2u(t)v(t) dt. (7.2.2)

Интеграл выражения (7.2.2) для двух вещественных сигналов является фундаментальной характеристикой, пропорциональной взаимной энергии сигналов. Его называют скалярным произведениемсигналов

П_uv= (u(t),v(t)) =u(t)v(t) dt = ||u||||v|| cos, (7.2.3)

Скалярное произведение обладает следующими свойствами

1. (u,v)  0;

2. (u,v) = (v,u);

3. (au,v) = a(u,v), где а – вещественное число;

4. (u+v, a) = (u,a) + (v,a).

Линейное пространство сигналов с таким скалярным произведением называется гильбертовым пространствомН. С учетом того, что cos1, в гильбертовом пространстве справедливо неравенство Коши-Буняковского

|П_uv|||u||||v||. (7.2.4)

Для комплексного гильбертова пространства скалярное произведение также представляет собой вещественное число и вычисляется по формуле

П_uv=u(t)v*(t) dtu*(t)v(t) dt. (7.2.3')

Из выражения (7.2.3) следует, что косинус угла между сигналами

cos = П_uv/(||u||||v||). (7.2.5)

При полной тождественности сигналов (равенстве амплитуд и временных координат) имеем = 0, cos= 1, и скалярное произведение становится равным энергии сигналов:

П_uv=u(t)²dtv(t)²dt||u||²||v||².

Дискретные сигналы обычно рассматриваются в пространстве Евклида(обозначение пространства - R₂). Скалярное произведение двух сигналов в пространстве Евклида:

П_uv= (u_k,v_k) =u_kv_k,

где n - размерность пространства.

Взаимный энергетический спектр.Из очевидной однозначности энергии взаимодействия сигналов независимо от формы их математического представления (в динамической и частотной модели) следует выражение для скалярного произведения произвольных вещественных сигналов u(t) и v(t) через спектральные плотности сигналов U() и V() в комплексном гильбертовом пространстве:

П_uv= (1/2)U()V*() d(1/2)U*()V() d. (7.2.6)

Функции

W_uv() = U()V*(), W_vu() = U*()V(), W_uv() = W_vu*(), (7.2.7)

для которых справедливо выражение (7.2.6), называется взаимными энергетическими спектрамивещественных сигналов, и являются функциями распределения плотности энергии взаимодействия сигналов (мощности взаимодействия) по частоте.

В общем случае, за исключением спектров четных функций, взаимные энергетические спектры также являются комплексными функциями:

U() = A_u() + j B_u(), V() = A_v() + j B_v().

W_uv = A_uA_v+B_uB_v+j (B_uA_v - A_uB_v) = Re W_uv(w) + j Im W_uv(). (7.2.7')

С учетом четности реальной части и нечетности мнимой части энергетических спектров, интеграл мнимой части выражения (7.2.7') равен нулю, а, следовательно, скалярное произведение сигналов всегда является вещественным и неотрицательным, как и энергия сигналов:

П_uv= (1/2)W_uv() d(1/)Re W_uv() d.2.8)

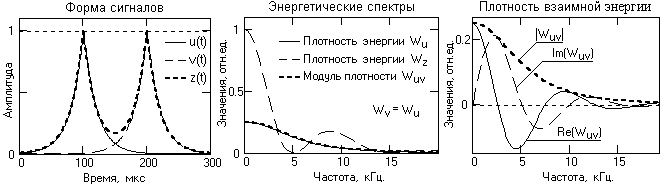
Рис. 7.2.1. Форма и энергетические спектры сигналов.

На рис. 7.2.1 приведена форма двух одинаковых сдвинутых во времени и частично перекрывающихся лапласовских импульсов u(t) и v(t), а также суммарный импульс z(t)=u(t)+v(t). Плотности энергии сигналов W(f) приведены в относительных единицах плотности энергии суммарного сигнала W_z(f) на нулевой частоте.

Как видно из графиков, плотности энергии сигналов являются вещественными неотрицательными функциями и содержат только реальные части. В отличие от них, плотность взаимной энергии сигналов является комплексной функцией, при этом модуль плотности по своим значениям на шкале частот соизмерим со средними значениями плотности энергии сигналов на этих частотах и не зависит от их взаимного расположения на временной оси. Для сигналов, одинаковых по форме, модуль взаимной плотности равен значениям плотности энергии сигналов.

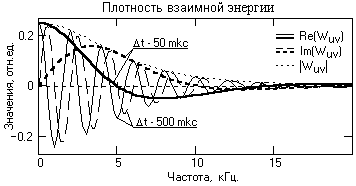
Рис. 7.2.2. Взаимные энергетические спектры сигналов.

На рис. 7.2.2 приведены плотности взаимной энергии тех же сигналов при разной величине временного сдвига t между сигналами. Однако при постоянном значении модуля взаимной энергии сигналов действительная и мнимая функции спектра мощности существенно изменяются при изменении сдвига между сигналами. При незначительной величине временного перекрытия сигналов частота осцилляций реальной и мнимой части плотности взаимной энергии достаточно велика, а относительный коэффициент затухания колебаний (уменьшение амплитудных значений от периода к периоду) достаточно мал. Соответственно, при вычислении скалярного произведения по формуле (7.2.8) положительные амплитудные значения осцилляций Re(W_uv) практически полностью компенсируются отрицательными значениями и результирующий интеграл, а равно и энергия взаимодействия сигналов (удвоенное значение скалярного произведения), близка к нулевой (стремится к нулю по мере увеличения сдвига между сигналами).

При увеличении степени взаимного перекрытия сигналов частота осцилляций плотности взаимной энергии уменьшается (t = 50 mkc на рис. 7.2.2) и основным по энергии реальной части спектра становится центральный низкочастотный пик, площадь которого не компенсируется площадью последующей отрицательной полуволны осцилляции. Соответственно, возрастает и энергия взаимодействия сигналов. При полном перекрытии сигналов (при нулевом фазовом угле между сигналами) осцилляции исчезают, и энергия взаимодействия сигналов максимальна.

3. Специальные математические функции для описания сигналов (rect-функция, sign-функция, sinc-функция, функция Хэвисайда (включения), функция Дирака (дельта-функция)).

4. Помехи радиоприёму. Классификация помех.

Помехи

Помехами обычно называют посторонние электрические возмущения, накладывающиеся на передаваемый сигнал и затрудняющие его прием. При большой интенсивности помех прием становится практически невозможным.

Классификация помех:

а) помехи от соседних радиопередатчиков (станций);

б) помехи от промышленных установок;

в) атмосферные помехи (грозы, осадки);

г) помехи, обусловленные прохождением электромагнитных волн через слои атмосферы: тропосферу, ионосферу;

д) тепловые и дробовые шумы в элементах радиоцепей, обусловленные тепловым движением электронов.

Математически сигнал на входе приемника можно представить либо в виде суммы передаваемого сигнала и помехи, и тогда помеху называют аддитивной, либо простошумом, либо в виде произведения передаваемого сигнала и помехи, и тогда такую помеху называютмультипликативной. Эта помеха приводит к значительным изменениям интенсивности сигнала на входе приемника и объясняет такие явления какзамирания.

Наличие помех затрудняет прием сигналов при большой интенсивности помех, распознавание сигнала может стать практически невозможным. Способность системы противостоять мешающему воздействию помехи носит название помехоустойчивости.

Внешние естественные активные помехи представляют собой шумы, возникающие в результате радиоизлучения земной поверхности и космических объектов, работы других радиоэлектронных средств. Комплекс мероприятий, направленных на уменьшение влияния взаимных помех РЭС, называется электомагнитной совместимостью. Этот комплекс включает в себя как технические меры совершенствования радиоаппаратуры, выбор формы сигнала и способа его обработки, так и организационные меры: регламентация частоты, разнесение РЭС в пространстве, нормирование уровня внеполосных и побочных излучений и др.

5. Разложение произвольного сигнала по заданной системе ортогональных функций. Условия ортогональности системы действительных функций. Интеграл Дирихле.

Функции φ(x) и _Ψ(x) называются ортогональными,если интеграл от их произведения равен нулю.

Рассмотрим ряд функций: . Система функцийназывается ортогональной, если на отрезке от "а" до "b" все функции попарно ортогональны.

Рассмотрим промежуток где n=m:

Если система функций при n=mимеет коэффициент, то эта функция является ортонормальной. Если ортогональная система функций не ортонормальна, то ее можно получить, произведя замену:

.

Рассмотрим систему ортогональных функций и некоторой произвольной функции. Разложим функциюв ряд по системе ортогональных функций, то есть предположим, что существует разложение вида:

Определим коэффициенты ряда. Для этого умножим обе части равенства [1] на и проинтегрируем. В результате получим:

Так как система функций ортогональна и ортонормальна, то получили равенство . Выразим С_n из уравнения:

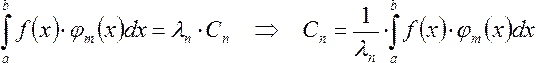
Ряд [1] называется обобщенным рядом Фурье, - коэффициентом ряда Фурье. Ряд [1] существует тогда и только тогда, когдаявляется периодической функцией, а система функций- является равномерно сходящейся.

7. Ряд Фурье. Разложение в ряд Фурье. Комплексная и тригонометрическая формы ряда Фурье. Понятие частотного спектра.