2. Представление сигналов в частотной области. Понятие спектра сигнала.

Каждый сигнал имеет своё представление, свой образ в частотной области.

Этот образ называется СПЕКТРОМ сигнала. Слово спектр происходит от латинского spectrum, что в буквальном переводе и означает представление, образ.

Например, гармонический сигнал вида S(t) = A sin (ωt+φ) представляется в частотной области единственным значением на оси частот.

Рис 3. Спектр синусоидального сигнала.

В математике известна теорема, носящая имя великого французского математика Жана Фурье, согласно которой любой периодический сигнал с периодом T может быть представлен рядом Фурье (гармоническим рядом).

Другими словами можно сказать, любой, самый сложный периодический сигнал можно представить совокупностью простых гармонических сигналов.

Возьмём, например, последовательность прямоугольных импульсов, длительность которых равна половине периода (такой сигнал называется МЕАНДР), а частота равна 50Гц. (рис 4.) Форма этого сигнала не очень похожа на синусоиду, коротая показана ниже вместе со своим спектром. Далее, на рис. 4в. показана основная гармоника на частоте 50 Гц , синусоида с частотой в три раза большей (150 Гц). но меньшей амплитуды и результат сложения этих двух сигналов. Видим, он по форме уже напоминает прямоугольные импульсы. Далее, на рис 4г., к первой и третьей гармоникам добавлена пятая, на частоте 250 Гц. Результат их сложения ещё более похож на исходный сигнал и так далее, чем больше гармоник мы будем суммировать, тем большую степень приближения к прямоугольным импульсам мы получим.

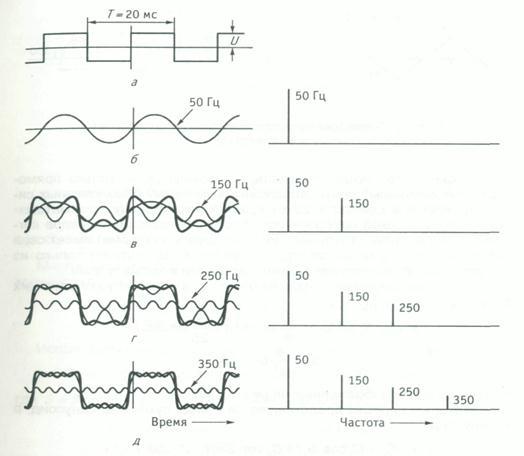
Рис. 4.Спектральный состав последовательности прямоугольных импульсов.

Аналитическая запись рассмотренного разложения имеет вид:

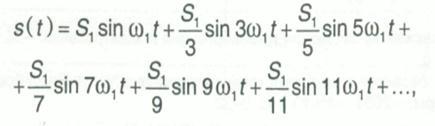
Или

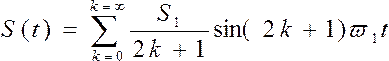
Чем больше сигнал отличается от гармонического, тем больше частотных составляющих в его спектральном представлении и тем меньше расстояние (разнос частот) между ними, т.е. шире спектр такого сигнала. На рис.5.показана синусоида ограниченная сверху и снизу т.е. несколько искажённая, а на рис.6 показан её спектр. Видим, спектр имеет высшие гармоники различной амплитуды.

Рис. 5.

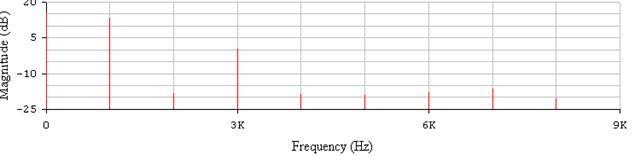
Рис. 6.

Таким образом, любое изменение формы сигнала неизбежно ведёт к изменению его спектра, и наоборот, любое изменение спектра сигнала приводит к изменению его спектра. Связь между временным и частотным представлением сигнала даёт теорема Фурье.

8. Преобразование Фурье. Прямое и обратное преобразование Фурье. Понятие амплитудного и фазового спектра сигнала.

Спектральный анализ - один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. Преобразование Фурье является математической основой, которая связывает временной или пространственный сигнал (или же некоторую модель этого сигнала) с его представлением в частотной области. Важную роль в спектральном анализе играют методы статистики, поскольку сигналы, как правило, имеют случайный характер или зашумлены при распространении или измерении. Если бы основные статистические характеристики сигнала были точно известны, или их можно было определить по конечному интервалу этого сигнала, то спектральный анализ представлял бы собой отрасль "точной науки". Однако, в действительности по отрезку сигнала можно получить только оценку его спектра. Поэтому практика спектрального анализа - некое ремесло (или искусство?) достаточно субъективного характера. Различие между спектральными оценками, получаемыми в результате обработки одного и того же отрезка сигнала разными методами, можно объяснить различием допущений, принятых относительно данных, различными способами усреднения и т .п. Если априори характеристики сигнала не известны, нельзя сказать какие из оценок лучше.

Преобразование Фурье - математическая основа спектрального анализа.

Пара преобразований Фурье. Спектральная плотность сигнала

Пусть сигнал s(t) задан в виде непериодической функции, причем он существует только на интервале (t₁ ,t₂) (пример - одиночный импульс). Выберем произвольный отрезок времени T, включающий в себя интервал (t₁ ,t₂) (см. рис.1).

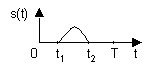
Рис. 1

Обозначим периодический сигнал, полученный из s(t), в виде s_T(t). Тогда для него можно записать ряд Фурье

где

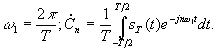
Подставим выражение для в ряд:

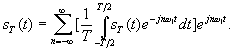
Для того, чтобы перейти к функции s(t) следует в выражении s_T(t) устремить период к бесконечности. При этом число гармонических составляющих с частотами  =n2 /T будет бесконечно велико, расстояние между ними будет стремиться к нулю ( к бесконечно малой величине: , амплитуды составляющих также будут бесконечно малы. Поэтому говорить о спектре такого сигнала уже нельзя, т.к. спектр становитсясплошным.

При предельном переходе в случае Т , имеем:

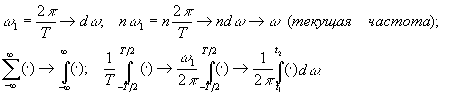
Таким образом, в пределе получаем

Внутренний интеграл является функцией частоты. Его называют спектральной плотностью сигнала, или частотной характеристикой сигнала и обозначают ,

т.е.

(*)

Пределы интегрирования можно для общности поставить бесконечными, так как все равно там, где s(t) равна нулю, и интеграл равен нулю.

Выражение для спектральной плотности называют прямым преобразованием Фурье. Обратное преобразование Фурье определяет временную функцию сигнала по его спектральной плотности:

(**)

рямое (*) и обратное (**) преобразования Фурье вместе называют парой преобразований Фурье. Модуль спектральной плотности определяет амплитудно-частотную характеристику (АЧХ) сигнала, а ее аргументназывают фазо-частотной характеристикой (ФЧХ) сигнала. АЧХ сигнала является четной функцией, а ФЧХ - нечетной.

Смысл модуля S() определяется как амплитуда сигнала (тока или напряжения), приходящаяся на 1 Гц в бесконечно узкой полосе частот, которая включает в себя рассматриваемую частоту  . Его размерность - [сигнал/частота].

9. Свойства преобразования Фурье. Свойства линейности, изменения масштаба времени, другие. Теореме о спектре производной. Теорема о спектре интеграла.

10. Дискретное преобразование Фурье. Помехи радиоприёму. Классификация помех.

Дискретное преобразование Фурье может быть получено непосредственно из интегрального преобразования дискретизаций аргументов (t_k = kt, f_n = nf):

S(f) =s(t) exp(-j2ft) dt, S(f_n) = ts(t_k) exp(-j2f_nkt), (6.1.1)

s(t) =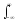S(f) exp(j2ft) df, s(t_k) = fS(f_n) exp(j2nft_k). (6.1.2)

Напомним, что дискретизация функции по времени приводит к периодизации ее спектра, а дискретизация спектра по частоте - к периодизации функции. Не следует также забывать, что значения (6.1.1) числового ряда S(f_n) являются дискретизаций непрерывной функции S'(f) спектра дискретной функции s(t_k), равно как и значения (6.1.2) числового ряда s(t_k) являются дискретизацией непрерывной функции s'(t), и при восстановлении этих непрерывных функций S'(f) и s'(t) по их дискретным отсчетам соответствие S'(f) = S(f) и s'(t) = s(t) гарантировано только при выполнении теоремы Котельникова-Шеннона.

Для дискретных преобразований s(kt)  S(nf), и функция, и ее спектр дискретны и периодичны, а числовые массивы их представления соответствуют заданию на главных периодах Т = Nt (от 0 до Т или от -Т/2 до Т/2), и 2f_N = Nf (от -f_N до f_N), где N – количество отсчетов, при этом:

f = 1/T = 1/(Nt), t = 1/2f_N = 1/(Nf), tf = 1/N, N = 2Tf_N. (6.1.3)

Соотношения (6.1.3) являются условиями информационной равноценности динамической и частотной форм представления дискретных сигналов. Другими словами: число отсчетов функции и ее спектра должны быть одинаковыми. Но каждый отсчет комплексного спектра представляется двумя вещественными числами и, соответственно, число отсчетов комплексного спектра в 2 раза больше отсчетов функции? Это так. Однако представление спектра в комплексной форме - не более чем удобное математическое представление спектральной функции, реальные отсчеты которой образуются сложением двух сопряженных комплексных отсчетов, а полная информация о спектре функции в комплексной форме заключена только в одной его половине - отсчетах действительной и мнимой части комплексных чисел в частотном интервале от 0 до f_N, т.к. информация второй половины диапазона от 0 до -f_N является сопряженной с первой половиной и никакой дополнительной информации не несет.

При дискретном представлении сигналов аргумент t_k обычно проставляется номерами отсчетов k (по умолчанию t = 1, k = 0,1,…N-1), а преобразования Фурье выполняются по аргументу n (номер шага по частоте) на главных периодах. При значениях N, кратных 2:

S(f_n)  S_n = s_k exp(-j2kn/N), n = -N/2,…,0,…,N/2. (6.1.4)

s(t_k)  s_k = (1/N)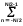S_n exp(j2kn/N), k = 0,1,…,N-1. (6.1.5)

Главный период спектра в (6.1.4) для циклических частот от -0.5 до 0.5, для угловых частот от - до . При нечетном значении N границы главного периода по частоте (значения f_N) находятся на половину шага по частоте за отсчетами (N/2) и, соответственно, верхний предел суммирования в (6.1.5) устанавливается равным N/2.

В вычислительных операциях на ЭВМ для исключения отрицательных частотных аргументов (отрицательных значений номеров n) и использования идентичных алгоритмов прямого и обратного преобразования Фурье главный период спектра обычно принимается в интервале от 0 до 2f_N (0  n  N), а суммирование в (6.1.5) производится соответственно от 0 до N-1. При этом следует учитывать, что комплексно сопряженным отсчетам S_n* интервала (-N,0) двустороннего спектра в интервале 0-2f_N соответствуют отсчеты S_N+1-n (т.е. сопряженными отсчетами в интервале 0-2f_N являются отсчеты S_n и S_N+1-n).

Пример: На интервале Т= [0,99],N=100, задан дискретный сигналs(k) =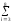(k-i) - прямоугольный импульс с единичными значениями на точкахkот 3 до 8. Форма сигнала и модуль его спектра в главном частотном диапазоне, вычисленного по формулеS(n) =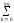s(k)exp(-j2kn/100) с нумерацией поnот -50 до +50 с шагом по частоте, соответственно,=2/100, приведены на рис. 6.1.1.

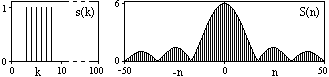
Рис. 6.1.1. Дискретный сигнал и модуль его спектра.

На рис. 6.1.2 приведена огибающая значений другой формы представления главного диапазона спектра. Независимо от формы представления спектр периодичен, в чем нетрудно убедиться, если вычислить значения спектра для большего интервала аргумента nс сохранением того же шага по частоте, как это показано на рис. 6.1.3 для огибающей значений спектра.

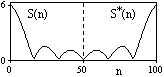
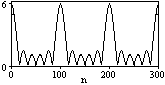
Рис. 6.1.2. Модуль спектра. Рис. 6.1.3. Модуль спектра.

На рис. 6.1.4. показано обратное преобразование Фурье для дискретного спектра, выполненное по формуле s'(k) =(1/100)S(n)exp(j2kn/100), которое показывает периодизацию исходной функцииs(k), но главный периодk={0,99} этой функции полностью совпадает с исходным сигналомs(k).

Рис. 6.1.4. Обратное преобразование Фурье.

Преобразования (6.1.4-6.1.5) называют дискретными преобразованиями Фурье (ДПФ). Для ДПФ, в принципе, справедливы все свойства интегральных преобразований Фурье, однако при этом следует учитывать периодичность дискретных функций и спектров. Произведению спектров двух дискретных функций (при выполнении каких-либо операций при обработке сигналов в частотном представлении, как, например, фильтрации сигналов непосредственно в частотной форме) будет соответствовать свертка периодизированных функций во временном представлении (и наоборот). Такая свертка называется циклической (см. раздел 6.4) и ее результаты на концевых участках информационных интервалов могут существенно отличаться от свертки финитных дискретных функций (линейной свертки).

Из выражений ДПФ можно видеть, что для вычисления каждой гармоники нужно N операций комплексного умножения и сложения и соответственно N² операций на полное выполнение ДПФ. При больших объемах массивов данных это может приводить к существенным временным затратам. Ускорение вычислений достигается при использовании быстрого преобразования Фурье.

Помехи

Помехами обычно называют посторонние электрические возмущения, накладывающиеся на передаваемый сигнал и затрудняющие его прием. При большой интенсивности помех прием становится практически невозможным.

Классификация помех:

а) помехи от соседних радиопередатчиков (станций);

б) помехи от промышленных установок;

в) атмосферные помехи (грозы, осадки);

г) помехи, обусловленные прохождением электромагнитных волн через слои атмосферы: тропосферу, ионосферу;

д) тепловые и дробовые шумы в элементах радиоцепей, обусловленные тепловым движением электронов.

Математически сигнал на входе приемника можно представить либо в виде суммы передаваемого сигнала и помехи, и тогда помеху называют аддитивной, либо простошумом, либо в виде произведения передаваемого сигнала и помехи, и тогда такую помеху называютмультипликативной. Эта помеха приводит к значительным изменениям интенсивности сигнала на входе приемника и объясняет такие явления какзамирания.

Наличие помех затрудняет прием сигналов при большой интенсивности помех, распознавание сигнала может стать практически невозможным. Способность системы противостоять мешающему воздействию помехи носит название помехоустойчивости.

Внешние естественные активные помехи представляют собой шумы, возникающие в результате радиоизлучения земной поверхности и космических объектов, работы других радиоэлектронных средств. Комплекс мероприятий, направленных на уменьшение влияния взаимных помех РЭС, называется электомагнитной совместимостью. Этот комплекс включает в себя как технические меры совершенствования радиоаппаратуры, выбор формы сигнала и способа его обработки, так и организационные меры: регламентация частоты, разнесение РЭС в пространстве, нормирование уровня внеполосных и побочных излучений и др.

11. Дискретизация непрерывных сигналов. Теорема Котельникова (отсчётов). Понятие частоты Найквиста. Понятие интервала дискретизации.

Дискретизация аналоговых сигналов. Ряд Котельникова

Всякое непрерывное сообщение s(t), занимающее конечный интервал времени Т_с , может быть передано с достаточной точностью конечным числом N отсчетов (выборок) s(nT), т.е. последовательностью коротких импульсов, разделенных паузой.

Дискретизация сообщений по времени – процедура, состоящая в замене несчетного множества мгновенных значений сигнала их счетным (дискретным) множеством, которое содержит информацию о значениях непрерывного сигнала в определенные моменты времени.

При дискретном способе передачи непрерывного сообщения можно сократить время, в течение которого канал связи занят передачей этого сообщения, с Т_с до , где- длительность импульса, применяемого для передачи выборки; можно осуществить одновременную передачу по каналу связи нескольких сообщений (временное уплотнение сигналов).

Наиболее простым является способ дискретизации, основанный на теореме В.А. Котельникова, сформулированной для сигналов с ограниченным спектром (теорема отсчетов):

если наивысшая частота в спектре функции s(t) меньше, чем F_m, то функция s(t) полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга не более, чем на секунд и может быть представлена рядом:

.

(1)

Здесь величина обозначает интервал между отсчетами на оси времени, а

- время выборки, - значение сигнала в момент отсчета.

Ряд (1) называется рядом Котельникова, а выборки (отсчеты) сигнала {s(nT)} иногда называют временным спектром сигнала.

Функция

обладает следующими свойствами:

а) в точке t=nT функция равна 1, т.к. в этой точке аргумент функции равен 0, а значение ее равно 1;

б) в точках t=kT, функция, т.к. аргумент синуса в этих точках равен, а сам синус равен нулю;

в) спектральная плотность функции u_n(nT)равномерна в полосе частот и равна. Этот вывод сделан на основе теоремы взаимности частоты и времени пары преобразований Фурье. ФЧХ спектральной плотности линейна и равна(в соответствии с теоремой о сдвиге сигнала). Таким образом,

.

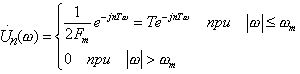Временное и частотное представления функции u_n(t) даны на рис.3.

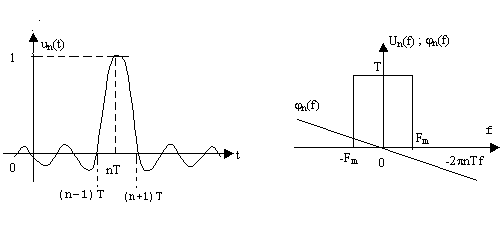
Рис. 3

Графическая интерпретация ряда Котельникова представлена на рис.4.

Рис. 4

Ряд Котельникова (1) обладает всеми свойствами обобщенного ряда Фурье с базисными функциями u_n(nT), и поэтому определяет функцию s(t) не только в точках отсчета, но и в любой момент времени.

Интервал ортогональности функции u_nравен бесконечности. Квадрат нормы

.

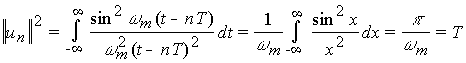Коэффициенты ряда, определяемые по общей формуле для ряда Фурье, равны (с использованием равенства Парсеваля):

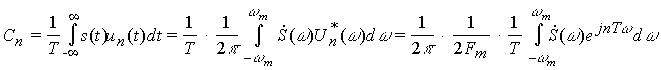
Так как

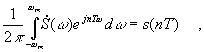
следовательно

При ограничении спектра сигнала конечной наивысшей частотой ряд (1) сходится к функции s(t) при любом значении t.

Если взять интервал Т между выборками меньшим, чем , то ширина спектра базисной функции будет больше ширины спектра сигнала, следовательно точность воспроизведения сигнала будет выше, особенно в случаях когда спектр сигнала не ограничен по частоте и наивысшую частотуF_m приходится выбирать из энергетических или информационных соображений, оставляя неучтенными “хвосты” спектра сигнала.

При увеличении расстояния между выборками () спектр базисной функции становится уже спектра сигнала, коэффициентыC_nбудут являться выборками другой функции s₁(t), спектр которой ограничен частотой .

Если длительность сигнала T_cконечна, то полоса его частот равна строго бесконечности, т.к. условия конечных длительности и полосы несовместимы. Однако практически всегда можно выбрать наивысшую частоту так, чтобы “хвосты” содержали либо малую долю энергии, либо слабо влияли на форму аналогового сигнала. При таком допущении число отсчетов N на времени Т_с будет равно Т_с/Т, т.е. N=2F_mT_c. Ряд (1) в этом случае имеет пределы 0, N.

Число N иногда называют числом степеней свободы сигнала, или базой сигнала. С увеличением базы точность восстановления аналогового сигнала из дискретного увеличивается.

12. Временные и частотные характеристики линейных радиотехнических цепей. Понятие импульсной характеристики. Понятие переходной характеристики. Понятие входной и передаточной частотной характеристики.

При рассмотрении радиотехнических сигналов было установлено, что сигнал может быть представлен как во временной (динамическое представление), так и в частотной(спектральное представление) областях. Очевидно, при анализе процессов преобразования сигналов цепи также должны иметь соответствующие описания временными или частотными характеристиками.

Начнём с рассмотрения временных характеристик линейных цепей с постоянными параметрами. Если линейная цепь осуществляет преобразование в соответствии с оператором и на вход цепи подаётся сигналв виде дельта-функции (на практике очень короткий импульс), то выходной сигнал (реакция цепи)

(5.5)

называется импульсной характеристикой цепи. Импульсная характеристика составляет основу одного из методов анализа преобразования сигналов, который будет рассмотрен ниже.

Если на вход линейной цепи поступает сигнал , т.е. сигнал вида “единичный перепад”, то выходной сигнал цепи

(5.6)

называется переходной характеристикой.

Между импульсом и переходной характеристикой существует однозначная связь. Так как дельта-функция (см. подраздел 1.3):

,

то подставляя это выражение в (5.5), получим:

. (5.7)

В свою очередь переходная характеристика

. (5.8)

Перейдём к рассмотрению частотных характеристик линейных цепей. Применим к входному и выходномусигналам прямое преобразование Фурье

,

.

Отношение комплексного спектра выходного сигнала к комплексному спектру входного сигнала называется комплексным коэффициентом передачи

(5.9)

Из этого следует, что

. (5.10)

Таким образом, оператором преобразования сигнала линейной цепью в частотной области служит комплексный коэффициент передачи.

Представим комплексный коэффициент передачи в виде

, (5.11)

где исоответственно модуль и аргумент комплексной функции. Модуль комплексного коэффициента передачикак функция частоты называетсяамплитудно-частотной характеристикой (АЧХ), а аргумент –фазочастотной характеристикой (ФЧХ). Амплитудно-частотная характеристика является чётной, а фазочастотная характеристика – нечётной функцией частоты .

Врменные и частотные характеристики линейных цепей связаны между собой преобразованием Фурье

, (5.12)

, (5.13)

что вполне объяснимо, поскольку они описывают один и тот же объект – линейную цепь.

13. Анализ воздействия детерминированных сигналов на линейные цепи с постоянными параметрами. Временной, частотный, операторный методы.
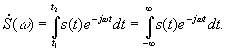
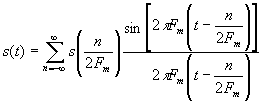