
- •1. Понятие сигнала.
- •Энергетические характеристики сигналов
- •Энергетические спектры сигналов [1].
- •2. Представление сигналов в частотной области. Понятие спектра сигнала.
- •Прохождение сигналов через линейные цепи с постоянными параметрами.
- •2.1. Определение линейной цепи.
- •2.2. Дельта - функция - как пример пробного сигнала.
- •Временной и спектральный методы анализа передачи сигналов через линейные цепи.
- •Взаимная и автокорреляционные функции сигнала
- •Общие определения
Взаимная и автокорреляционные функции сигнала
Корреляционный анализ используется при необходимости оценить временные свойства сигнала без применения спектрального анализа, например, для оценки скорости изменения или длительности сигнала, временной связи (корреляции) одного сигнала с другим.
Взаимная корреляционная функцияопределяет временную связь двух сигналов во времени. Если сигналы не зависимы друг от друга, их корреляционная функция равна нулю. Чем шире корреляционная функция, тем большая степень связи двух сигналов друг с другом.
Взаимная корреляционная функция определяется соотношением

Пример
получения взаимной корреляционной
функции показан на рис.1. Значение
корреляционной функции в любой момент
xопределяется площадью пересечения
функций![]() и
сдвинутой копии
и
сдвинутой копии![]() .
.

Рис. 1
Взаимная корреляционная функция не обязательно симметрична и её максимум может оказаться не в точке x=0.
Автокорреляционной функцией (АКФ) ограниченного во времени сигнала называется выражение вида

где x – временной сдвиг исходного сигнала.
Геометрический
смысл автокорреляционной функции
заключается в определении площади
пересечения функции
![]() и
её копии, сдвинутой на времяx(Рис.2)
и
её копии, сдвинутой на времяx(Рис.2)

Рис. 2
Изменяя
время сдвига xдо тех пор, пока сигнал
и его копия перестанут пересекаться (в
данном случае![]() ),
получим АКФ
),
получим АКФ![]() .
Очевидно, что при изменении знака сдвига
при одинаковой его величине функция
автокорреляции одинакова, т.е.
.
Очевидно, что при изменении знака сдвига
при одинаковой его величине функция
автокорреляции одинакова, т.е.![]() ,
что говорит о четном её характере. Ясно,
что приx=0автокорреляционная
функция имеет максимум, при этом
,
что говорит о четном её характере. Ясно,
что приx=0автокорреляционная
функция имеет максимум, при этом

а в свою очередь полная энергия сигнала равна

Таким образом, максимум автокорреляционной функции определяет полную энергию сигнала. При увеличении сдвига x АКФ убывает до нуля.
Примеры
Прямоугольный импульс (рис. 3).
|
|
а)
б)
Сдвинутый на
в)
Площадь произведения равна
г) АКФ |
|
Рис. 3 | |
Для x>0 имеем

и интеграл для x<0

Максимум
АКФ равен энергии сигнала:
![]()
2) Треугольный импульс. Построение АКФ показано на рис. 4.

Рис. 4
Произведение
представляет собой нелинейную функцию
от t.
Полная энергия сигнала (максимум АКФ)
равна![]() Длительность
АКФ равна удвоенной длительности
сигнала.
Длительность
АКФ равна удвоенной длительности
сигнала.
3. Сигнал представляет собой пачку из идентичных импульсов, расположенных на равных расстояниях друг относительно друга. АКФ также будет иметь вид пачки импульсов, удаленных друг от друга на те же расстояния, причем амплитуды импульсов в пачке будут убывать от центра к краям (см. рис. 5)

Рис. 5
14. Общая теория радиосигналов. Понятие узкополосного и широкополосного сигнала. Понятие частоты и фазы радиосигнала, их взаимосвязь. Понятие базы сигнала.
Общие определения
К радиосигналам относят высокочастотные почти гармонические (квазигармонические) колебания, в которых амплитуда или мгновенная частота или фаза медленноменяются по некоторому закону. Процесс изменения одного или нескольких параметров высокочастотного гармонического колебания называется модуляцией. В системе радиосвязи закон модуляции должен соответствовать закону изменения передаваемого низкочастотного сообщения.
Частота исходного высокочастотного гармонического колебания называется несущей частотой. Устройство, создающее это колебание, называется генератором несущей частоты или задающим генератором. К нему предъявляются высокие требования к стабильности амплитуды и частоты.
Несущее колебание имеет вид
![]()
где
![]() -амплитуда,
-амплитуда,![]() -частота,0-начальная
фаза.
-частота,0-начальная
фаза.
Различают амплитудную (АМ),частотную (ЧМ) и фазовую (ФМ) модуляцию. При амплитудной модуляции по закону низкочастотного сигнала меняется мгновенная амплитуда, при частотной модуляции – частота, при фазовой модуляции – фаза. Бывают и смешанные виды модуляции. В отдельный класс можно выделить импульсные виды модуляции и манипуляции, при которых происходит дискретное изменение параметра высокочастотного колебания.
Основные понятия о базе сигнала
В системах
связи используется такое понятие как
база сигнала, которое определяется
теоремой Котельникова. То есть исходя
из нее любой сигнал с финитным спектром
можно разложить на несколько отсчетов,
взятых через интервалы времени
 ,
где F
– верхняя граничная частота спектра
сигнала (рис. 1).
,
где F
– верхняя граничная частота спектра
сигнала (рис. 1).

Рис. 1. Пояснение к тереме Котельникова
В данном случае, если сигнал существует только в течение времени - Т‚ то количество отсчетов будет равно
 . (2.1)
. (2.1)
Эта величина определяет
размерность пространства, в котором
представляется сигнал координатами
(отсчетами мгновенных значений через
временные интервалы
 ).
В этой связи в теории связи эту величину
называют базой сигнала:
).
В этой связи в теории связи эту величину
называют базой сигнала:
 .
(2.2)
.
(2.2)
В иных случаях
говорят, что величина
 определяет
базис сигнала, т.е. количество осей
координат, в котором раскладывается
сигнал.
определяет
базис сигнала, т.е. количество осей
координат, в котором раскладывается
сигнал.
Сравнительный анализ узкополосных и
широкополосных сигналов
В действующих
системах связи, использующих дискретные
сигналы значение базы для простых
сигналов равно
 (рис. 2). Этот же сигнал можно представить
в виде сложного сигнала, база которого
будет равна -
(рис. 2). Этот же сигнал можно представить
в виде сложного сигнала, база которого
будет равна - (см. рис. 2).
(см. рис. 2).

Рис. 2. Простой и сложный сигналы
База сигнала указывает на зависимость ширины спектра от длительности сигнала. В случае применения простых сигналов ширина его спектра мала:
 , (2.3)
, (2.3)
в связи с чем такие сигналы называют узкополосными. Следует заметить, что спектр узкополосного сигнала после модуляции не намного отличается от спектра первичного сигнала.
Для сложных сигналов
 ,
,  (2.4)
(2.4)
В этом случае спектр сложного сигнала как до, так и после модуляции намного превышает спектр первичного сигнала, поэтому его принято называть широкополосным.
Для начала вспомним понятие полной фазы радиосигнала
|
|
(2) |
а также понятие мгновенной частоты радиосигнала, как производной от полной фазы:
|
|
(3) |
Сигналы, у которых изменяется полная фаза в соответствии с модулирующим сигналом называются сигналами с угловой модуляцией.
Для начала рассмотрим сигналы с фазовой модуляцией (phase modulation PM). У сигналов с PM полная фаза изменяется в соответствии с модулирующим сигналом:
|
|
(4) |
где
![]() называется
индексом фазовой модуляции или девиацией
фазы, а модулирующий сигнал по модулю
не превосходит единицы
называется
индексом фазовой модуляции или девиацией
фазы, а модулирующий сигнал по модулю
не превосходит единицы![]()
Тогда комплексная огибающая PM сигнала имеет вид:
|
|
(5) |
а сам радиосигнал может быть представлен следующим образом:
|
|
(6) |
Теперь рассмотрим сигнал с частотной модуляцией (frequency modulation FM). В отличии от PM при частотной модуляции происходит изменение мгновенной частоты радиосигнала:
|
|
(7) |
где
![]() называется
индексом частотной модуляции или
девиацией частоты, а модулирующий сигнал
по модулю не превосходит единицы
называется
индексом частотной модуляции или
девиацией частоты, а модулирующий сигнал
по модулю не превосходит единицы![]() Тогда
полную фазу радиосигнала можно рассчитать
как интеграл от мгновенной частоты:
Тогда
полную фазу радиосигнала можно рассчитать
как интеграл от мгновенной частоты:
|
|
(8) |
Сигнал с FM имеет вид:
|
|
(9) |
где
![]() -
произвольная постоянная интегрирования
полной фазы (8). Обратите внимание, что
абсолютно не верно подставлять выражение
для мгновенной частоты вместо несущей
частоты в выражение для полосового
сигнала:
-
произвольная постоянная интегрирования
полной фазы (8). Обратите внимание, что
абсолютно не верно подставлять выражение
для мгновенной частоты вместо несущей
частоты в выражение для полосового
сигнала:
|
|
(10) |
так
как
![]() Правильным
является выражение (9)!
Правильным
является выражение (9)!
16. Сигналы с внутриимпульсной модуляцией. Сигналы с линейной частотной модуляцией. Фазо-кодо-манипулированные сигналы. Математические модели, спектральные характеристики, особенности применения.





Фазо-кодо-манипулированные импульсы (ФКМ)
ФКМ радиоимпульсы характеризуются скачкообразным изменением фазы внутри импульса по определенному закону, например (рис. 1.66):
код
трехэлементного сигнала
закон изменения фазы
трехэлементный сигнал
Рис. 1.66
или семиэлементный сигнал (рис. 1.67)
Таким образом, можно сделать выводы:
· АЧС сигналов с ЛЧМ является сплошным.
· Огибающая АЧС определяется формой огибающей сигнала.
· Максимальное значение АЧС определяется энергией сигнала, которая в свою очередь, прямопропорциональна амплитуде и длительности сигнала.
·
Ширина спектра равна
![]() где
где![]() девиация
частоты и не зависит от длительности
сигнала.
девиация
частоты и не зависит от длительности
сигнала.
·
База сигнала (коэффициент широкополостности)
![]() может
бытьn>>1.Поэтому
ЛЧМ сигналы называют широкополосными.
может
бытьn>>1.Поэтому
ЛЧМ сигналы называют широкополосными.

Рис. 1.67
ФКМ
радиоимпульсы длительностью
![]() представляют
собой совокупность следующих друг за
другом без интервалов
представляют
собой совокупность следующих друг за
другом без интервалов![]() элементарных
радиоимпульсов,длительность каждого
из них одинакова и равна
элементарных
радиоимпульсов,длительность каждого
из них одинакова и равна .Амплитуды
и частоты элементарных импульсов
одинаковы, а начальные фазы могут
отличаться на
.Амплитуды
и частоты элементарных импульсов
одинаковы, а начальные фазы могут
отличаться на![]() (или
какое-либо другое значение). Закон (код)
чередования начальных фаз определяется
назначением сигнала. Для ФКМ радиоимпульсов,
используемых в радиолокации разработаны
соответствующие коды, например:
(или
какое-либо другое значение). Закон (код)
чередования начальных фаз определяется
назначением сигнала. Для ФКМ радиоимпульсов,
используемых в радиолокации разработаны
соответствующие коды, например:
+1, +1, -1 - трехэлементные коды
 -два
варианта четырехэлементного кода
-два
варианта четырехэлементного кода
+1 +1 +1, -1, -1, +1, -2 - семиэлементный код
Спектральную плотность кодированных импульсов определяют,используя свойство аддитивности преобразований Фурье, в виде суммы спектральных плотностей элементарных радиоимпульсов.
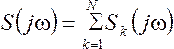
Графики АЧС для трехэлементного и семиэлементного импульсов приведены на рисунке 1.68

Рис. 1.68
Как видно из приведенных рисунков, ширина спектра ФКМ радиосигналов определяется длительностью элементарного радиоимпульса

или
 .
.
Коэффициент
широкополостности

,где N-количество элементарных радиоимпульсов.
ФКМ сигналы применяются в широкополосных системах связи, радиолокации, в устройствах идентификации обьектов.
6. Понятие нормированной функции. Понятие ортонормированной системы функций.
Нормирование метрических параметров. Норма функций в пространстве L2[a, b] определяется выражением:
||s(t)||
=![]() .
.
Нетрудно заключить, что чем больше интервал [a, b] в этой формуле, тем больше (при прочих равных условиях) будет значение нормы. При анализе и сравнении сигналов (как аналоговых, так и многомерных дискретных) такое понятие не всегда удобно, и вместо него очень часто используют понятие нормы, нормированной относительно длины интервала[a, b]. Для символьного обозначения нормирования будем применять знак :
||s(t)||
=![]() ,
||sn||
=
,
||sn||
= .
.
Метрика сигналов (расстояние между сигналами) при аналогичном нормировании:
d
(s(t), v(t)) =![]() ,
d
(sn,
vn)
=
,
d
(sn,
vn)
=

Эти выражения применяются для вычисления среднеквадратического расхождения сигналов или среднеквадратической погрешности выполнения какой-либо операции при сравнении ее результата с теоретически ожидаемым или априорно известным.
Нормированное скалярное произведение сигналов:
б
s(t), v(t)
=![]() s(t)v(t) dt = ||s(t)||
||v(t)||
cos .
s(t)v(t) dt = ||s(t)||
||v(t)||
cos .
б
sn,
vn
=(1/N)![]() sn
vn
= ||sn||
||sn||
cos .
sn
vn
= ||sn||
||sn||
cos .
Косинус угла (коэффициент корреляции) между сигналами – функциями не изменяет своих значений при вычислении как по нормированным, так и по ненормированным значениям скалярного произведения и нормы сигналов (значения нормировки в числителе и знаменателе выражения (2.1.8) сокращаются). Взаимная перпендикулярность функций определяется аналогично взаимной перпендикулярности векторов условием нулевого значения скалярного произведения.
Норма, метрика и скалярное произведение периодических функций обычно нормируются на длину главного периода Т.
Ортогональные сигналы. Два сигнала называются ортогональными (orthogonal), если имеют нулевое скалярное произведение
б
u(t), v(t)
=![]() u(t)v(t)
dt = 0.
u(t)v(t)
dt = 0.
Соответственно, два таких сигнала в своем функциональном пространстве являются взаимно перпендикулярными (угол между сигналами равен = 90о), полностью независимыми друг от друга (некоррелированными, r = cos , и имеют нулевую энергию взаимодействия (Euv = 0).
На рисунке 2.3.1 приведены примеры взаимно ортогональных сигналов. Нулевое скалярное произведение двух левых сигналов обеспечивается их формой (равна нулю сумма положительных и отрицательных значений произведения сигналов), а двух правых - взаимным расположением (ненулевые значения сигналов не имеют общих координат).

Рис. 2.3.1. Ортогональные сигналы.
Попутно заметим, что энергия и мощность суммы ортогональных сигналов обладают свойством аддитивности, т.к. имеют нулевое значение скалярного произведения и, соответственно, энергии взаимодействия.
Ортонормированный базис пространства. Множество сигналов – векторов {vk, k = 1, 2, …, N} в N-мерном декартовом пространстве при единичной норме и выполнении условий взаимной ортогональности:
б
vm,
vn
=
![]() (2.3.1)
(2.3.1)
могут быть приняты в качестве ортонормированного базиса данного пространства. Выражение (2.3.1) обычно записывается в следующей форме:
б vm, vn = mn, (2.3.1')
где mn – импульс Кронекера, равный правой части выражения (2.3.1).
С использованием ортонормированного базиса любой произвольный сигнал можно представить в виде линейной комбинации взвешенных базисных векторов:
s = c1v1 + c2v2 + … + cNvN,
где весовое значение сk определяется проекцией вектора s на соответствующее координатное направление:
ck = s, vk .
При распространении данных положений на функциональное пространство L2[a, b] в качестве координатного базиса пространства мы должны использовать совокупность функций {u0(t), u1(t), u2(t), …}, в пределе - бесконечную, которая должна быть системой ортогональных функций {uk(t), k=0, 1, 2, …}, т.е. все функции на этом отрезке должны быть взаимно ортогональны:
б
um(t),
un(t)
=![]() um(t)
un(t)
dt = 0, m = 1, 2, ... ; n = 1, 2, ... ; m
n.
um(t)
un(t)
dt = 0, m = 1, 2, ... ; n = 1, 2, ... ; m
n.
Система ортогональных функций на интервале [a, b] будет ортонормированной (orthonormal functions), если все функции системы при m=n имеют единичную норму, т.е. выполняются условия:
б
um(t),
um(t)
= ||um(t)||2
=![]() (um(t))2
dt = 1, ||um(t)||
= 1,
m
= 1, 2, ....
(um(t))2
dt = 1, ||um(t)||
= 1,
m
= 1, 2, ....
Эти условия можно записать в следующей обобщенной форме:
![]() um(t)·un*(t)
dt = m,n.
um(t)·un*(t)
dt = m,n.
Система ортогональных функций всегда может быть превращена в ортонормированную путем нормировки, т.е. деления всех функций на их норму.


