Проверка адекватности линейной регрессионной модели

Линейная регрессионная модель называется адекватной, если предсказанные по ней значения переменной y согласуются с результатами наблюдений. Грубая оценка адекватности модели может быть приведена непосредственно по графику остатков, т.е. по сумме квадратов разностей между наблюдениями и соответствующими в значениями y, полученными по уравнению регрессии.

Если модель адекватна, то остатки являются реализациями случайных ошибок наблюдений , которые в силу предполжений независимы, имеют нормальное распределение с нулевыми математическими ожиданиями и одинаковыми дисперсиями .Проверка выполнения этих предположений различными статистическими методами лежит в основе оценки адекватности по графику остатков.

Пусть для каждого или некоторых значений переменной х имеются несколько повторных наблюдений случайной величины у .

Пусть повторные наблюдения получены при значениях х₁,х₂,……х_m причем при х = х_i произведено n_i наблюдений у, где =n – объем выборки наблюдений. Обозначим y_ij – результаты повторных наблюдений переменной у при х = х_i i=1,2,…,m ; j=1,2,…,n_i ;

Если модель адекватна наблюдениям , то cредние n_i наблюдений , т.е. , i=1,2,…,m должны бить близки к вычисленным значениям у (х_i).

Следственно сумма квадратов Q_n = является мерой неадекватности модели.

Остаточная сумма квадратов Q_e может быть разбита на две составляющих:

, (26)

где - сумма чистой ошибки

(27)

Если линейная регрессия адекватна данным , то статистики Q_p и Q_n независимы и имеют распределение ² соответственно с m-2 и n-m степенями свободы.

Отношение этих статистик имеет распределение Фишера, т.е.:

(28)

Если , то модель адекватна наблюдениям иможно использовать в качестве оценки дисперсии, в противном случае нужно использовать другую модель (нелинейную).

Пример.

Найти оценки параметров линейной регрессии по следующим данным:

x	1	1	1,3	2	2	3	3	2,7	2,7	4,3	4,3	4,3	4,7	5,0	5,0
y	0,5	0,1	0,7	0,5	1,2	1,2	1,7	0,9	2,2	1,1	1,7	2,5	2,4	2,0	2,2

Проверить адекватность линейной регрессии по этим данным. Принять

= 0,05. Выпишем результаты повторных наблюдений:

Таблица 11

	1	xi	1	2	3	2,7	4,3	5,0	
	2	yij	0,5 0,1	0,5 1,2	1,2 1,7	0,5 2,2	1,1 1,7 2,5	2,0 2,2	17,8
	3	ni	2	2	2	2	3	2	13
	4		0,3	0,85	1,45	1,55	1,73	2,1
	5	yij^2	0,25 0,01	0,25 1,44	1,44 2,89	0,81 4,84	1,4 2,89 6,25	4,0 4,84	31,12
	6	yi=yij	0,6	1,7	2,9	3,1	5,3	4,2
	7	xi yi	0,6	3,4	8,7	8,37	22,79	21,0	64,08
	8	xi ni	2	4	6	5,4	12,9	10,0	40,3
	9	xi ni^2	2	8	18	14,58	55,47	50	148,05

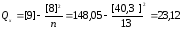
По формулам (17), (18) находим

, .

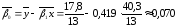Находим остаточную сумму квадратов

, ,Q_e = 6,74 – 4,059 – 2,681.

Для парных повторных наблюдений при вычислении Q_p удобно пользоваться соотношением

.

Используя это соотношение , а также то, что при x = 4,3 имеем 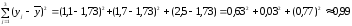, по формуле (27) получим

.

Используя тождество (26) находим сумму квадратов, обусловленную неадекватностью:

Выборочное значение статистики (28) равно

.

Так как квантиль 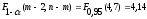>=0,296, то линейная регрессия (модель) адекватна результатам наблюдений.