Факторный анализ

Основные положения

Факторный анализ – это один из новых разделов многомерного статистического анализа. Первоначально этот метод разрабатывался для объяснения корреляции между исходными параметрами. Результатом корреляционного анализа является матрица коэффициентов корреляции. При малом числе признаков (переменных) можно провести визуальный анализ этой матрицы. С ростом числа признаков (10 и более) визуальный анализ не даст положительных результатов. Оказывается, что все многообразие корреляционных связей можно объяснить действием нескольких обобщенных факторов, которые являются функциями исследуемых параметров, при этом сами факторы могут быть неизвестны, но их можно выразить через исследуемые признаки. Основоположником факторного анализа является американский ученый Л.Терстоун.

Современные статистики под факторным анализом понимают совокупность методов, которые на основе реально существующей связи между признаками позволяет выявить латентные (скрытые) обобщающие характеристики организационной структуры и механизмы развития изучаемых явлений и процессов.

Пример: предположим, что n автомобилей оценивается по 2 признакам:

x₁ – стоимость автомобиля,

x₂ – длительность рабочего ресурса мотора.

При условии коррелированности x₁ и x₂ в системе координат появляется направленное и достаточно плотное скопление точек, формально отображаемое новыми осями и( Рис.5).

Рис.6

Характерная особенность F₁ и F₂ заключается в том, что они проходят через плотные скопления точек и в свою очередь коррелируют с x₁ x ₂.Максимальное

число новых осей будет равно числу элементарных признаков. Дальнейшие разработки факторного анализа показали, что этот метод может быть с успехом применены в задачах группировки и классификации объектов.

Представление информации в факторном анализе.

Для проведения факторного анализа информация должна быть представлена в виде матрицы размером m x n:

Строки матрицы соответствуют объектам наблюдений (i=), а столбцы – признакам (j=).

Признаки, характеризующие объект имеют разную размерность. Для того, чтобы их привести к одной размерности и обеспечить сопоставимость признаков матрицу исходных данных обычно нормируют, вводя единый масштаб. Самым распространенным способом нормировки является стандартизация. От переменных переходят к переменным

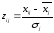, где

- среднее значение j признака,

- среднеквадратическое отклонение.

Такое преобразование называется стандартизацией.

Основная модель факторного анализа

Основная модель факторного анализа имеет вид:

, j=

z_{j –} j-й признак (величина случайная);

F₁, F₂, …, F_p – общие факторы (величины случайные, нормально распределенные);

u_j – характерный фактор;

_j1, _j2, …, _jp – факторы нагрузки, характеризующие существенность влияния каждого фактора (параметры модели, подлежащие определению);

d_j – нагрузка характерного фактора .

Общие факторы имеют существенное значение для анализа всех признаков. Характерные факторы показывают, что он относится только к данному -му признаку, это специфика признака, которая не может быть выражена через факторы. Факторные нагрузки _j1, _j2, …, _jp характеризуют величину влияния того или иного общего фактора в вариации данного признака. Основная задача факторного анализа – определить факторные нагрузки. Дисперсию S_j² каждого признака, можно разделить на 2 составляющие:

1. первая часть обуславливает действие общих факторов – общность h_j²;

2. вторая часть обуславливает действие характерного фактора –характерность - d_j² .

Все переменные представлены в стандартизованном виде, поэтому дисперсия -го признака S_j² = 1.

Если общие и характерные факторы не коррелируют между собой, то дисперсию j-го признака можно представить в виде:

_{где - доля дисперсии признака, приходящаяся наk-ый фактор.}

Полный вклад какого-либо фактора в суммарную дисперсию равен:

, .

Вклад всех общих факторов в суммарную дисперсию:

.

Результаты факторного анализа удобно представить в виде таблицы.

	Факторные нагрузки	Общности
А	a11 a 21 … a p1 a 12 a 22 … a p2 … … … … a 1m a 2m … a pm	…
Вклады факторов	V1 V2 … Vp	V

А - матрица факторных нагрузок. Ее можно получить различными способами, в настоящее время наиболее распространение получил метод главных компонент или главных факторов.

Вычислительная процедура метода главных факторов.

Решение задачи с помощью главных компонент сводится к поэтапному преобразованию матрицы исходных данных X :

Рис.7

Х- матрица исходных данных;

Z – матрица стандартизированных значений признаков ,

R – матрица парных корреляций :

- диагональная матрица собственных (характеристических) чисел,

,

_j находят решением характеристического уравнения

_Е–единичная матрица,

_j – показатель дисперсии каждой главной компоненты ,

при условии стандартизации исходных данных , тогда=m

U – матрица собственных векторов , которые находят из уравнения:

Реально это означает решение m систем линейных уравнений для каждого

,т.е. каждому собственному числу соответствует система уравнений.

Затем находят V- матрицу нормированных собственных векторов.

,

Матрицу факторного отображения А вычисляют по формуле:

Затем находим значения главных компонент по одной из эквивалентных формул:

Пример:

Совокупность из четырех промышленных предприятий оценена по трем характерным признакам:

• среднегодовая выработка на одного работника х₁;

• уровень рентабельности х₂;

- уровень фондоотдачи х_3.

Результат представлен в стандартизированной матрице Z:

По матрице Z получена матрица парных корреляций R:

1. Найдем определитель матрицы парных корреляций(например методом Фаддеева):

2. Построим характеристическое уравнение:

3. Решая это уравнение найдем:

Таким образом исходные элементарные признаки х₁, х₂, х₃ могут быть обобщены значениями трех главных компонент, причем:

F₁ объясняет примерно всей вариации,

F₂ - , аF₃ -

Все три главные компоненты объясняют вариации полностью на 100%.

4. Собственные векторы матрицы парных корреляций найдем решением трех систем линейных уравнений. Для =1,798 получим систему:

Решая эту систему находим:

, ,

Аналогично строятся системы для ₂ и ₃. Для ₂ решение системы:

, ,,

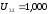для ₃:

, ,

Матрица собственных векторов U принимает вид:

5. Каждый элемент матрицы разделим на сумму квадратов элементов j-го

столбца, получим нормированную матрицу V.

Отметим , что должно выполнятся равенство =E.

6. Матрицу факторного отображения получим из матричного соотношения

=

	F1	F2	F3
	0,776	-0,130	0,308
	0,904	-0,210	-0,420
	0,616	0,902	0,236

По смыслу каждый элемент матрицы А представляет частные коэффициенты матрицы корреляции между исходным признаком x_j и главными компонентами F_r . Поэтому все элементы .

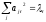Из равенства следует условиеr- число компонент .

Полный вклад каждого фактора в суммарную дисперсию признаков равен:

Модель факторного анализа примет вид:

Найдем значения главных компонент (матрицу F) по формуле

Центр распределения значений главных компонент находится в точке (0,0,0).

Далее аналитические выводы по результатам расчетов следуют уже после принятия решения о числе значащих признаков и главных компоненти определения названий главным компонентам. Задачи распознавания главных компонент, определения для них названий решают субъективно на основе весовых коэффициентовиз матрицы отображенияА.

Рассмотрим вопрос формулировки названий главных компонент.

Обозначим w₁ – множество незначимых весовых коэффициентов, в которое включаются близкие к нулю элементы,,

w₂ - множество значимых весовых коэффициентов,

w₃ – подмножество значимых весовых коэффициентов, не участвующих в формировании названия главной компоненты.

w₂ - w₃ – подмножество весовых коэффициентов, участвующих в формировании названия.

Вычисляем коэффициент информативности для каждого главного фактора

Набор объяснимых признаков считаем удовлетворительным, если значения коэффициентов информативности лежат в пределах 0,75-0,95.

a₁₁=0,776 a₁₂=-0,130 a₁₃=0,308

a₁₂=0,904 a₂₂=-0,210 a₂₃=-0,420

а₃₁=0,616 а₃₂=0,902 а₃₃=0,236

Для j=1 w₁= ,w₂={a₁₁,a₂₁,a₃₁},

.

Для j=2 w₁={ a₁₂, a₂₂ }, w₂={ а₃₂},

Для j=3 w₁={ а₃₃}, w₂={a₁₃,a₃₃},

Значениями признаков x₁, x₂, x₃ определяется состав главной компоненты на 100%. при этом наибольший вклад признакаx₂, смысл которого-рентабельность. корректным для названия признака F₁ будет эффективность производства.

F₂ определяется компонентой x₃ (фондоотдача), назовем ее эффективность использования основных производственных средств.

F₃ определяется компонентами x₁ ,x₂ –в анализе может не рассматриваться т.к. она объясняет всего 10% общей вариации.

Литература.

1. Попов А.А.

Excel: Практическое руководство, ДЕСС КОМ.-М.-2000.

2. Дьяконов В.П., Абраменкова И.В. Mathcad7 в математике, физике и в Internet. Изд-во « Номидж», М.-1998, раздел 2.13. Выполнение регрессии.

3. Л.А. Сошникова, В.Н. Томашевич и др. Многомерный статистический анализ в экономике под ред. В.Н. Томашевича.- М. –Наука, 1980.

4. Колемаев В.А., О.В. Староверов, В.Б. Турундаевский Теория вероятностей и математическая статистика. –М. – Высшая школа- 1991.

5. К Иберла. Факторный анализ.-М. Статистика.-1980.

№10

Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны

Пусть генеральные совокупности X и Y распределены нормально, причем их дисперсии известны (например из предшествующего опыта или найдены теоретически). По независимым выборкам объемов n и m, извлеченным из этих совокупностей, найдены выборочные  средние x_в и y_в.

 Требуется по выборочным средним при заданном уровне значимости проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой, т. е. Н₀: М(X) = М(Y).

Учитывая, что выборочные средние являются несмещенными оценками генеральных средних, т. е. М(x_в) = М(X) и М(y_в) = М(Y), нулевую гипотезу можно записать так: Н₀: М(x_в) = М(y_в).

Таким образом, требуется проверить, что математические ожидания выборочных средних равны между собой. Такая задача ставится, потому что, как правило, выборочные средние являются различными. Возникает вопрос: значимо или незначимо различаются выборочные средние?

Если окажется, что нулевая гипотеза справедлива, т. е. генеральные средние одинаковы, то различие выборочных средних незначимо и объясняется случайными причинами и, в частности, случайным отбором объектов выборки.

Если нулевая гипотеза будет отвергнута, т. е. генеральные средние неодинаковы, то различие выборочных средних значимо и не может быть объяснено случайными причинами. А объясняется тем, что сами генеральные средние (математические ожидания) различны.

В качестве проверки нулевой гипотезы примем случайную  величину.

Критерий Z – нормированная нормальная случайная величина. Действительно, величина Z распределена нормально, так как является линейной комбинацией нормально распределенных величин X и Y; сами эти величины распределены нормально как выборочные средние, найденные по выборкам, извлеченным из генеральных совокупностей; Z – нормированная величина, потому что М(Z) = 0, при справедливости нулевой гипотезы D(Z) = 1, поскольку выборки независимы.

Критическая область строится в зависимости от вида конкурирующей гипотезы.

Первый случай. Нулевая гипотеза Н₀:М(X)=М(Y). Конкурирующая гипотеза Н₁: М(X) ¹М(Y).

В этом случае строят двустороннюю критическую область исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости .

Наибольшая мощность критерия (вероятность попадания критерия в критическую область при справедливости конкурирующей гипотезы) достигается тогда, когда «левая» и «правая» критические точки выбраны так, что вероятность попадания критерия в каждый интервал критической области равна:

P(Z < zлев.кр)=a¤2,                                                      

P(Z > zправ.кр)=a¤2.                                                 (1)

Поскольку Z – нормированная нормальная величина, а распределение такой величины симметрично относительно нуля,  критические точки симметричны относительно нуля.

Таким образом, если обозначить правую границу двусторонней критической области через zкр, то левая граница -zкр.

Итак, достаточно найти правую границу, чтобы найти саму двустороннюю критическую область Z < -zкр, Z > zкр и область принятия нулевой гипотезы (-zкр, zкр).

Покажем, как найти zкр – правую границу двусторонней критической области, используя функцию Лапласа Ф(Z). Известно, что функция Лапласа определяет вероятность попадания нормированной нормальной случайной величины, например Z, в интервале (0;z):

Р(0 < Z<z)=Ф(z)                                                 (2)

Так как распределение Z симметрично относительно нуля, то вероятность попадания Z в интервал (0; ¥) равна 1/2. Следовательно, если разбить этот интервал точкой zкр на интервал (0, zкр) и (zкр, ¥), то по теореме сложения Р(0< Z < zкр)+Р(Z > zкр)=1/2.

В силу (1) и (2) получим Ф(zкр)+a/2=1/2. Следовательно,  Ф(zкр) =(1-a)/2.

Отсюда заключаем: для того чтобы найти правую границу двусторонней критической области ( zкр), достаточно найти значение аргумента функции Лапласа, которому соответствует значение функции, равное (1-a)/2.

Тогда двусторонняя критическая область определяется неравенствами Z < – zкр, Z > zкр, или равносильным неравенством ½Z½ > zкр, а область принятия нулевой гипотезы неравенством – zкр < Z < zкр или равносильным неравенством çZ ç< zкр.

Обозначим значение критерия, вычисленное по данным наблюдений, через zнабл и сформулируем правило проверки нулевой гипотезы.

 

Правило.

1. Вычислить наблюдаемое значение критерия

2. По таблице функции Лапласа найти критическую точку по равенству Ф(zкр)=(1-a)/2.

3. Если ç zнабл ç < zкр – нет оснований отвергнуть нулевую гипотезу.

Если ç zнабл ç> zкр – нулевую гипотезу отвергают.

Второй случай. Нулевая гипотеза Н0: M(X)=M(Y). Конкурирующая гипотеза Н1: M(X)>M(Y).

На практике такой случай имеет место, если профессиональные соображения позволяют предположить, что генеральная средняя одной совокупности больше генеральной средней другой. Например, если введено усовершенствование технологического процесса, то естественно допустить, что оно приведет к увеличению выпуска продукции.

 В этом случае строят правостороннюю критическую область исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости:

P(Z> zкр)=a.                                                          (3)

Покажем, как найти критическую точку при помощи функции Лапласа. Воспользуемся соотношением

P(0<Z< zкр)+P(Z> zкр)=1/2.

В силу (2) и (3) имеем Ф(zкр)+a=1/2. Следовательно,  Ф(zкр)=(1-2a)/2.

Отсюда заключаем, для того чтобы найти границу правосторонней критической области (zкр), достаточно найти значение функции Лапласа, равное (1-2a)/2. Тогда правосторонняя критическая область определяется неравенством Z > zкр, а область принятия нулевой гипотезы – неравенством Z < zкр.

Правило.

1. Вычислить наблюдаемое значение критерия zнабл.

2. По таблице функции Лапласа найти критическую точку из равенства Ф(zкр)=(1-2a)/2.

3. Если Z_набл < z_кр – нет оснований отвергнуть нулевую гипотезу. Если Z_набл > z_кр – нулевую гипотезу отвергаем.

Третий случай. Нулевая гипотеза Н0: M(X)=M(Y). Конкурирующая гипотеза Н1: M(X)<M(Y).

В этом случае строят левостороннюю критическую область исходя из требования, вероятность попадания критерия в эту область, в пред-

положении справедливости нулевой гипотезы, была равна принятому уровню значимости P(Z < z’кр)=a, т.е. z’кр= – zкр. Таким образом, для того чтобы найти точку z’кр, достаточно сначала найти “вспомогательную точку” zкр а затем взять найденное значение со знаком минус. Тогда левосторонняя критическая область определяется неравенством Z < -zкр, а область принятия нулевой гипотезы – неравенством Z > -zкр.

Правило.

1. Вычислить Zнабл.

2. По таблице функции Лапласа найти “вспомогательную точку” zкр по равенству Ф(zкр)=(1-2a)/2, а затем положить z’кр = -zкр.

3. Если Zнабл > -zкр, – нет оснований отвергать нулевую гипотезу.

Если Zнабл < -zкр, – нулевую гипотезу отвергают.