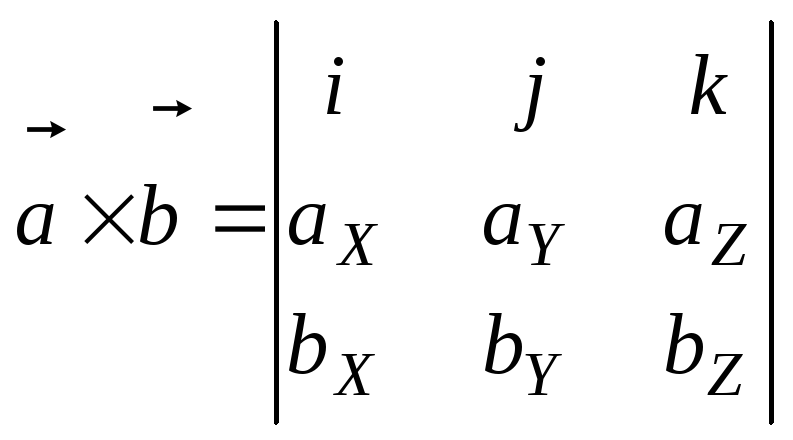Добавил:

jarenoeletto Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Кубанский государственный технологический университет

Предмет:

Высшая математика

Файл:

Линейная и векторная алгебра.doc

Скачиваний:

132

Добавлен:

01.10.2016

Размер:

1.23 Mб

Скачать

☆

<<< < Предыдущая 12 / 52 3 4 5 > Следующая >>>

2.2. Решение систем трех линейных уравнений с тремя неизвестными

Для системы составляем главный определитель

и вычисляем его.

Затем составляем дополнительные определители

и вычисляем их.

По правилу Крамера решение системы находят по формулам

; ; ,если

Примеры:

Вычислим:

По формулам Крамера находим:

Ответ: (1; 2; 3)

Вычислим:

Так как главный определитель , а хотя бы один дополнительный не равен нулю (в нашем случае ), то решения у системы нет.

Вычислим:

Так как все определители равны нулю, то система имеет бесконечное множество решений, которое можно найти так

Решите самостоятельно системы:

а) б)

Ответ: а) ( 1; 2; 5 ) б) ;;

Практическое занятие № 3 на тему:

Скалярное произведение двух векторов и его приложение

1. Если дан и, то скалярное произведение находим по формуле:∙

2.Если, то скалярное произведение этих двух векторов находим по формуле

Примеры:

1. Даны два вектора и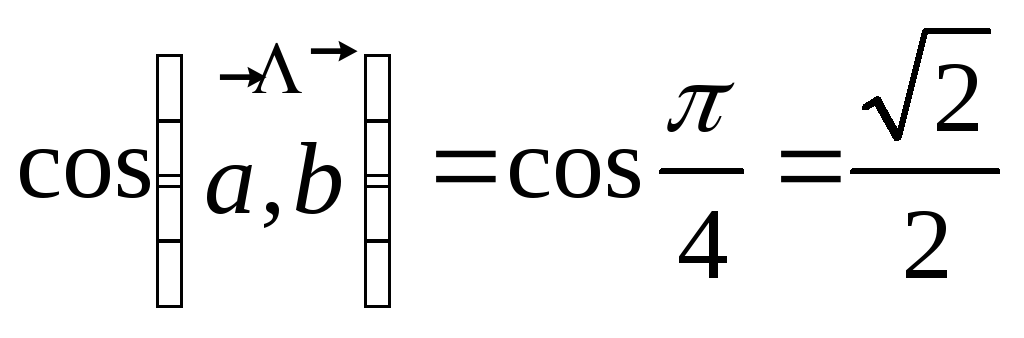

Их скалярное произведение находим так:

2. Даны два вектора:

={2;3;–4} ={1; –5; 6}

скалярное произведение находят так:

3.,

3.1 Нахождение работы постоянной силы на прямолинейном участке пути

Примеры:

1) Под действием силы в 15Н тело переместилось по прямой на 2 метра. Угол между силой и направлением перемещения =60⁰. Вычислить работу силы по перемещению тела.

Дано:

Решение:

2) Дано:

Найти А.

Решение:

3) Из точки М(1; 2; 3) в точку N(5; 4; 6) переместилось тело под действием силы 60Н. Угол между направлением силы и вектором перемещения =45⁰. Вычислить работу, совершаемую этой силой.

Решение: находим вектор перемещения

Находим модуль вектора перемещения:

По формуле находим работу:

3.2 Определение ортогональности двух векторов

Два вектора ортогональны, если , то есть

так как

Примеры:

–не ортогональны

–ортогональны

3) Определить, при каком  векторы и взаимно-ортогональны.

Так как , то , значит

Решите самостоятельно:

а)

. Найти их скалярное произведение.

б) Вычислить, какую работу производит сила , если точка ее приложения, двигаясь прямолинейно, переместилась из точки M (5; -6; 1) в точку N (1; -2; 3)

в) Определить, ортогональны ли вектора и

Ответы: а) 1 б) 16 в) да

3.3.Нахождение угла между векторами

Примеры:

. Найти .

Решение:

Находим

подставляем в формулу:

1). Даны вершины треугольника А(3; 2; –3), В(5; 1; –1), С(1; –2; 1). Найти угол при вершине А.

Решение:

Находим

Подставим в формулу:

Решите самостоятельно:

Даны вершины треугольника А(3; 5; -2), В(5; 7; -1), С(4; 3; 0). Определить внутренний угол при вершине А.

Ответ: 90^о

Практическое занятие № 4 на тему:

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ И ЕГО ПРИЛОЖЕНИЕ.

Формула для нахождения векторного произведения двух векторов:

имеет вид

Примеры:

1) Найти модуль векторного произведения:

Решение:

Составим определитель и вычислим его (по правилу Саррюса или по теореме о разложении определителя по элементам первой строки).

1-ый способ: по правилу Саррюса

2-й способ: разложим определитель по элементам первой строки.

2) Найти модуль векторного произведения:

4.1. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА, ПОСТРОЕННОГО НА ДВУХ ВЕКТОРАХ.

Примеры:

1) Вычислить площадь параллелограмма, построенного на векторах

Решение.

2). Найти векторное произведение и его модуль

Ответ:

4.2. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА

Пример: даны вершины треугольника А(1; 0; -1), В(1; 2; 0), С(3; -1; 1). Вычислить площадь треугольника.

Решение:

Сначала найдем координаты двух векторов, выходящих из одной вершины.

Найдем их векторное произведение

найдем

4.3. ОПРЕДЕЛЕНИЕ КОЛЛИНЕАРНОСТИ ДВУХ ВЕКТОРОВ

Если вектора иколлинеарны, то

, т. е. координаты векторов должны быть пропорциональны.

Примеры:

а) Даны вектора:: , .

Они коллинеарны потому, что и

после сокращения каждой дроби получается соотношение

б) Даны вектора: .

Они не коллинеарны, потому, что или

Решите самостоятельно:

а) При каких значениях m и n вектора коллинеарны?

Ответ: ;

б) Найти векторное произведение и его модуль , .

Ответ: ,.

Практическое занятие № 5 на тему:

ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

Примеры:

Задача № 1. Найти уравнение прямой, проходящей через точку А(-2; 3) параллельно прямой

Решение:

1. Найдем угловой коэффициент прямой .

- это уравнение прямой с угловым коэффициентом и начальной ординатой (). Поэтому .

2. Так как прямые MN и АС параллельны, то их угловые коэффициенты равны, т.е. .

3. Для нахождения уравнения прямой АС воспользуемся уравнением прямой, проходящей через точку с данным угловым коэффициентом:

. В эту формулу вместо и подставим координаты точки А(-2; 3), вместо подставим – 3. В результате подстановки получим:

Ответ:

Задача №2. Найти уравнение прямой, проходящей через точку К(1; –2) параллельно прямой .

Решение:

1. Найдем угловой коэффициент прямой .

- это общее уравнение прямой, которое в общем виде задается формулой . Сравнивая уравнения и находим, что А = 2, В = –3. Угловой коэффициент прямой, заданной уравнением , находится по формуле . Подставив в эту формулу А = 2 и В = –3, получим угловой коэффициент прямой MN. Итак, .

2. Так как прямые MN и КС параллельны, то их угловые коэффициенты равны: .

3. Для нахождения уравнения прямой КС воспользуемся формулой уравнения прямой, проходящей через точку с данным угловым коэффициентом . В эту формулу вместо и подставим координаты точки К(–2; 3), вместо подставим . В результате подстановки получим:

Ответ:

Задача № 3. Найти уравнение прямой, проходящей через точку К(–1; –3) перпендикулярно прямой .

Решение:

1. – это общее уравнение прямой, которое в общем виде задается формулой .

и находим, что А = 3, В = 4.

Угловой коэффициент прямой, заданной уравнением , находится по формуле: . Подставив в эту формулу А = 3 и В = 4, получим угловой коэффициент прямой MN: .