
Физика учебное пособие НГТУ
.pdf
x2 |
2 |
x y |
cos |
y2 |
sin |
2 |
. |
(12.48) |
|||
|
|
|
|
|
|
|
|||||
2 |
A B |
B |
2 |
|
|||||||
A |
|
|
|
|
|
|
|
||||
Определим форму траектории для некоторых частных случаев.
1. Разность фаз равна нулю. В этом случае уравнение (12.48) принимает вид
x |
|
y 2 |
0 , |
|||
|
|
|
|
|
||
|
|
|||||
A |
|
B |
|
|||
откуда получается уравнение прямой |
B x . |
|
||||
y |
(12.49) |
|||||
|
|
|
A |
|
||
Результирующее движение точки является гармоническим колебанием, происходящим вдоль этой прямой с частотой и амплитудой, равной
A2 B2 (рис. 12.13).
2. Разность фаз равна . Уравнение (12.49) принимает вид
|
x |
|
y 2 |
0 , |
|
||
|
|
|
|
|
|
||
A |
|
|
|||||
|
|
B |
|
|
|||
откуда получается уравнение прямой |
y B x . |
|
|||||
|
(12.50) |
||||||
|
|
|
|
|
A |
|
|
Результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 12.14).
|
y |
|
y |
|
|
|
А |
|
А |
|
|
|
|
В |
В |
|
|
В |
0 |
x |
0 |
В |
x |
|
А |
|
А |
|
|
|
Рис. 12.13 |
|
Рис. 12.14 |
|
|
3. При 2 уравнение (12.48) переходит в
x2 |
y2 |
|
|||
|
|
|
|
1, |
(12.51) |
2 |
B |
2 |
|||
A |
|
|
|
||
т.е. в уравнение эллипса, оси которого совпадают с координатными осями, причем полуоси эллипса равны соответствующим амплитудам колебаний. При равенстве амплитуд А и В эллипс вырождается в окружность.
130

12.5.Примеры решения задач
1.Некоторая точка движется вдоль оси х по закону x Asin 2 ωt π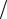 4 .
4 .
Найти:
а) амплитуду и период колебаний; изобразить график x(t) ;
б) проекцию скорости Vx как функцию координаты x ; изобразить график Vx (x) .
Дано |
4 |
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x Asin 2 ωt π |
|
Преобразуем функцию x(t) : |
|
|
|
|
|
|
|
|||||||||||||
а) график x(t) ; |
|
x Asin |
2 |
|
|
|
|
1 |
|
cos 2(ωt π |
4) |
|||||||||||
б) график Vx (x) . |
|
|
ωt π 4 A |
2 |
|
|
|
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A |
|
A |
cos(2ωt π 2) |
|
A |
|
A |
sin 2ωt. |
|
|
|
|||||||
|
2 |
2 |
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
Откуда амплитуда колебаний x0 |
|
|
A |
, период колебаний |
T |
2π |
|
|
π |
. |
||||||||||||
2 |
2ω |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
||||
Найдем проекцию скорости Vx как функцию времени t:
Vx dxdt A cos 2 t .
Тогда
Vx2 (A )2 cos2 2 t (A )2 1 sin2 2 t .
Учитывая, что sin(2 t) 1 |
|
x |
, получаем: |
|||||
A/ 2 |
||||||||
|
|
|
|
|
|
|
||
|
|
|
x |
|
2 |
V 2 |
|
|
1 |
|
|
|
|
|
x |
1 |
|
|
A/ 2 |
( A )2 |
||||||
|
|
|
|
|
|
|||
– уравнение эллипса на плоскости (x, Vx ) .
Графики x(t) и Vx (x) приведены на рисунках.
131

|
|
|
|
x |
|
|
|
|
|
||
X |
|
V x |
|
А |
|
||
A |
|||
|
|||
А/2 






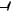
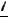






O |
А |
x |
|
X |
O |
|
2 |
t |
2. Материальная точка массой m 1 г совершает колебания вдоль оси x по
закону x Asin 0t . Амплитуда колебаний |
A 10 см, период колебаний |
T 4 с. В момент времени t 1 с найти: |
|
а) силу F, действующую на данную точку; б) кинетическую энергию Т точки.
Дано
m 1 г=1·10-3 кг;
x Asin 0t ;
A 10 см=1·10-1м;
T 4 с; t 1 с
F(t) ? Т(t) ?
Тогда
Решение
Согласно второму закону Ньютона, записанному в проекции на ось X, вдоль которой материальная точка массой m совершает гармонические колебания,
Fx max ,
где Fx – проекция на ось X силы, действующей на данную точку, ax – проекция ускорения точки:
ax d 2 x |
A 02 sin 0t . |
dt 2 |
|
Fx mA 02 sin 0t .
Следовательно, величина силы, действующей на точку,
F Fx mA 02 sin 0t .
Здесь круговая частота колебаний 0 2T , 0 2 с-1.
Кинетическая энергия материальной точки определяется по формуле
Т mV2 x2 ,
132
где Vx dxdt A 0 cos 0t – скорость точки. Таким образом,
|
|
Т |
mA2 2 |
|
|
|
|
|
||
|
|
|
2 |
0 cos2 0t . |
|
|||||
В момент времени t 1 с |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
F 1 10 3 |
|
|
2 |
|
|
0,25 мН; |
||||
0,1 |
|
sin |
2 |
1 |
||||||
|
|
|
|
2 |
|
|
|
|
||
Т |
1 10 3 |
0,12 ( / 2)2 |
|
2 |
|
|
0 Дж. |
|||
|
2 |
|
|
cos |
|
|
1 |
|||
|
|
|
|
|
|
|
2 |
|
|
|
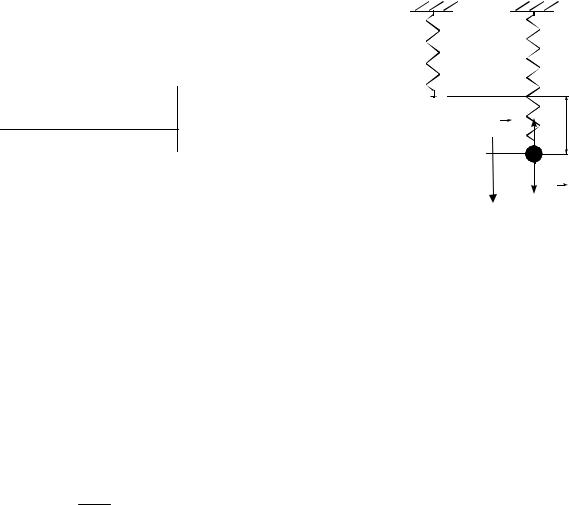
3. Неподвижное тело, подвешенное на пружинке, увеличивает ее длину на l 40 мм. Найти период малых вертикальных колебаний тела.
Дано Решение
l 40 мм =4·10-2м
T=?
В положении равновесия сила упругости Fупр , действующая на тело со стороны растя-
нутой на l 40 мм пружины, уравновешивается силой тяжести mg , где m – масса тела, поэтому
Fупр |
|
|
40мм |
l |
|
||
0 |
|
|
|
y |
mg |
|
|
|
|
|
l mg , |
(1) |
где – коэффициент жесткости пружины. Откуда |
|
mg . |
(2) |
l |
|
Выведем тело из положения равновесия и отпустим. Будучи освобожденным, тело начнет совершать вертикальные колебания относительно положения равновесия. Смещение тела из положения равновесия обозначим y. Запишем второй закон Ньютона в проекции на вертикальную ось y, направленную вниз:
may ( y l) mg , |
(3) |
где ay d 22y y . dt
С учетом (1) уравнение (3) примет вид
|
|
|
|
|
|
m y 0 . |
(4) |
||||
y |
|||||
Подставляя (2) в (4), получаем:
133





 3 , см и
3 , см и 6 , см.
6 , см.

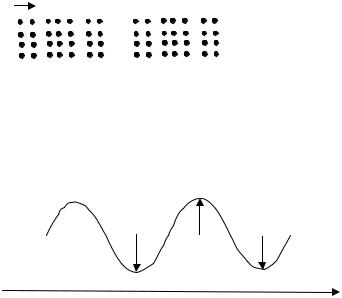
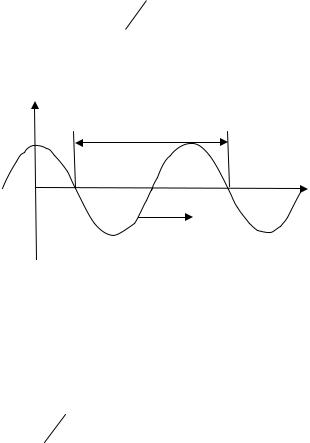
 сительно направления их распространения.
сительно направления их распространения. ных волн являются звуковые волны в газах. При распространении волны вдоль натяну-
ных волн являются звуковые волны в газах. При распространении волны вдоль натяну- жидкостях и газах могут распространяться только в виде продольных волн («волны сжатия»).
жидкостях и газах могут распространяться только в виде продольных волн («волны сжатия»).