Физика учебное пособие НГТУ

Рис. 4.4

снова переходит в кинетическую энергию тел.

Запишем законы сохранения импульса и механической энергии (рис. 4.3):

m1V1 m2V2 m1V1 m2V2 ,

m12V12 m22V22 m1V21 2 m22V2 2 .

Перепишем эти уравнения в следующем виде:

		V2 ) ,	m1	2	2		m2	2	2	) .
				(V1		)			V2
m1 (V1 V1 ) m2	(V2		2		V1		2	(V2

Учитывая равенства V12 V1 2 (V1 V1 )(V1 V1 ) , V2 2 V22 (V2 V2 )(V2 V2 ) , можно

сделать вывод, что V1 V1 V2 V2 .

Решая полученное уравнение совместно с записанным ранее законом сохранения импульса для соударяющихся тел, найдем скорости шаров после удара:

V1		m1 m2 V1 2m2V2 ;	V2		m2 m1 V2 2m1V1 .
		m1 m2			m1 m2

Особый интерес представляет случай, когда массы шаров одинаковы m1 = = m2. При этом условии получается, что V1 V2 и V2 V1 , т.е. происходит обмен

скоростями. В частности, если один из шаров до соударения покоился, то после удара он движется с такой же скоростью, какую имел первоначально другой шар, который после удара окажется неподвиж-

m	V1	V2		m	ным.
1
				2		Абсолютно неупругий центральный
					удар.
						Абсолютно неупругим называется удар,
			V
	m1	m2			при котором потенциальная энергия упругой
					деформации не возникает, а кинетическая энер-

x гия тел частично или полностью переходит в немеханические виды. Тела соединяются и продолжают двигаться дальше как единое целое

или останавливаются. Скорость совместного движения находится из закона со-

хранения импульса (рис. 4.4):

m1V1 m2V2 (m1 m2 )V ,

V m1V1 m2V2 .

m1 m2

Механическая энергия системы тел при абсолютно неупругом ударе не сохраняется. Часть механической энергии ∆E тел переходит в немеханические виды, например, выделяется в виде тепла Q:

m V 2			m V 2			(m m	)V 2		m m		2			2
	1 1		2 2			1 2			1
Q			2			2							(V1	V2 )	.
	2								2(m	m		)
									1		2

31

4.7.Примеры решения задач

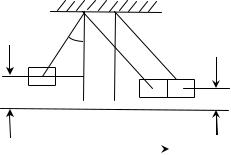
1.Два тела массой m1 и m2 подвешены на гибких, нерастяжимых и невесомых нитях длиной l каждая, как показано на рисунке. Тело m1 отклонили на

угол α и отпустили. Считая соударение тел абсолютно неупругим, а время соударения пренебрежимо малым, определить высоту h , на которую поднимутся тела после удара.

Дано

Решение

0

На уровне

линии

m1 , m2 ,

АВ, проходящей

через

С

l , ;

удар неупругий

центры масс тел в перво-

D

начальном состоянии, по-

h0

П=0

h

h =?

лагаем значение потенци- А

m1

m2

В

альной энергии П равной

x

нулю.

После неупругого взаимодействия оба тела поднимутся на высоту h . Считаем систему тел ( m1 , m2 , Земля) замкнутой (например, отсутствуют силы

трения о воздух, в подвеске и др.). После удара в системе действуют: силы тяжести, являющиеся консервативными, и силы натяжения нитей, которые работы по перемещению тел не совершают.

Закон сохранения механической энергии запишем в виде:

	(m m )gh (m			m )	V 2	,	(1)
					2
	1	2	1	2

где V – скорость, приобретенная телами за период кратковременного взаимо-

действия. Отсюда h	V 2	.
	2g
Скорость V находится из закона сохранения импульса:
		m1V1 m2V2			(m1 m2 )V ,		(2)
где V2 0(тело m2 до удара покоилось).
Тогда в проекции на ось x
		m1V1 (m1 m2 )V ,
откуда				m1V1
		V				.
			m m
				1	2
Неизвестная величина скорости V1					(скорость подлета тела m1		к телу m2 )

находится из закона сохранения механической энергии:

	m gh m			V12	,	V 2	2gh .
				2
	1	0	1			1	0

Величина h0 находится из прямоугольного треугольника СDО: h0 l l cos 2l sin2 / 2.

32

Искомая величина h			V 2		m2V 2				2l		m2		2
					1	1					1		sin / 2.
			2g		2g(m	m )2					(m m )2
					1	2	l				1	2
При m	= m	= m высота подъема тел h								sin2 / 2.
1	2					2

2. Допустим, что в предыдущей задаче происходит абсолютно упругое соударение. Чему в этом случае равна скорость второго тела сразу после удара и высота h , на которую оно поднимется?

Дано

m1 , m2 , l , ;

удар упругий h =? V2 =?

Решение

Обозначим искомую скорость V2 . При абсолютно уп-

ругом соударении выполняются закон сохранения импульса и закон сохранения механической энергии. Используя из предыдущей задачи обозначение скорости подлета первого тела ко второму V1 , запишем указанные законы:

m1V1 m2V2 m1V1 m2V2 , m12V12 m22V22 m12V1 2 m22V2 2 ,

где V2 0 ; V1, V2 - скорости тел после соударения.

В проекции на ось x :

m1V1 m1V1 m2V2 ,

m1V12 m1V1 2 m2V22 .

После преобразования система уравнений принимает вид

m1	(V1	V1) m2V2 ,		(1)
m1	(V12 V1 2 ) m2V22 .			(2)

Разложив разность квадратов в уравнении (2), с учетом (1) получаем соотношение:

V1 V2 V1 .			(3)
Решая совместно уравнения (1) и (3), получаем
V2	2m1V1	.
	m1 m2
Значение V1 берем из решения предыдущей задачи:
V1	2gh0 ,

где h0 2l sin2 / 2.

В итоге искомая величина скорости второго тела после удара равна

33

V2 4m1 gl sin / 2. m1 m2

Высота h , на которую поднимется тело m2 после абсолютно упругого соударения, определяется из закона сохранения энергии:

m2 gh m2 V22 ,

2

откуда h V22 .

2g

Окончательно имеем h				8m2l				2
				1		sin			/ 2.
				(m m )2
		= m		1	2
При m	= m		получаем h 2l sin2				/ 2 .
1	2

3. Тело массой т = 1 кг скользит сначала по наклонной плоскости высотой h = 1 м и длиной склона S1 = 10 м, а затем по горизонтальной поверхности. Коэффициент трения на всем пути μ = 0,05. Найти: а) кинетическую энергию Т тела у основания плоскости; б) скорость V тела у основания плоскости; в) расстояние S2, пройденное телом по горизонтальной поверхности до остановки.

Дано:

Решение

m = 1 кг;

По

закону

сохране-

h= 1 м;

ния энергии:

S1= 10 м;

Анеконс.сил E .

μ = 0,05

В

нашем

случае

в

а) Т = ?

П=0

верхней

точке траектории

б) V = ?

тело обладает энергией Т=0, П=mgh; у основания плоскости:

в) S2 = ?

mV 2

T

, П=0. Следовательно,

2

mV

2

mgh A

,

mV 2

mgh F

S ;

2

тр

2

тр

1

mV 2

S 2

h2

а) T

. С учетом того, что F N mg cos , где cos

1

, по-

2

тр

S1

лучаем T mg h

S12 h2

1 9,8 1,0 0,05 100 1 4,9 Дж;

б) V

2T

2 4,9

3,1 м/c;

m

1

в) на участке S2 по теореме об изменении кинетической энергии тела энергия, которую тело имеет у основания наклонной плоскости, идет на совершение ра-

34

боты	против				силы трения	на		горизонтальной поверхности, т.е.
T F	S		mgS		, откуда найдем S			T		4,9	10 м.
								mg		0,05 1 9,8
тр		2		2		2

4. Автомобиль массой m=2 т равномерно движется в гору с уклоном 4 м на каждые 100 м пути. Коэффициент трения μ = 0,08. Найти работу А, совершаемую двигателем автомобиля на пути S=3 км, и мощность N развиваемую двигателем, если известно, что путь S был пройден за время t = 4 мин.

Дано

Решение

m = 2000 кг;

В случае равномерного дви-

h= 4 м;

жения автомобиля его ускорение

l= 100 м;

а = 0. Тогда, согласно второму за-

μ = 0,08;

кону Ньютона, в проекции на ось x

S =3000м;

сила тяги двигателя:

t = 240 с

F Fтр mg sin ,

а) A = ?

или F mg cos sin , где sin h l ,

cos 1 h2

2 .

б) N = ?

l

Тогда

а) работа постоянной силы F на пути S будет определяться по формуле

4

2

4

A FS mgS cos sin 2000 9,8 3000 0,08

1

7 МДж;

1002

100

б) мощность двигателя, согласно определению, N

A

7 106

29,2 кВт.

t

240

5.ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА

5.1. Момент инерции

При изучении вращения твердого тела пользуются понятием момента инерции. Физически момент инерции является мерой инертности тела при вращательном движении.

Скалярная величина J mr2 называется моментом инерции материаль-

ной точки m относительно оси вращения z (r − кратчайшее расстояние от точ-

ки до оси вращения). Единицей измерения момента инерции в системе СИ яв-

ляется килограмм - метр в квадрате (кг·м2).

Моментом инерции J системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс mi материальных

точек системы на квадраты их расстояний ri2 до рассматриваемой оси:

35

n

J mi ri2 .

i 1

В случае непрерывного распределения масс сумма сводится к интегралу:

J r	2	dm ,					2
				1				3
m
где интегрирование производится по всей массе
тела (по всему объему).					Рис. 5.1
Момент инерции сложного тела JТ равен
сумме моментов инерции его составных частей (рис. 5.1):
		JТ = J1+ J2 + J3.
Если известен момент инерции тела относительно оси, проходящей через
его центр масс, то момент инерции относительно другой									О´
параллельной оси определяется теоремой Штейнера:
момент инерции тела J относительно оси вращения					С			а
ОО´ равен моменту его инерции JС относительно парал-
лельной оси, проходящей через центр масс С тела, сло-
женному с произведением массы m на квадрат расстоя-									О
ния a между осями (рис. 5.2):					Рис. 5.2
J = JC + ma2.

Величина момента инерции тела зависит от массы тела и её распределения относительно оси вращения.

Приведем значения моментов инерции некоторых однородных тел (табл. 5.1), расчет которых представлен в п.5.6.

Таблица 5.1

Твердое тело

Положение оси

Момент инерции

вращения

1. Прямой тонкий стержень

Ось перпендикулярна

стержню

и

ml 2

длиной l

проходит через его середину

12

2. Прямой тонкий стержень

Ось перпендикулярна

стержню

и

ml 2

длиной l

проходит через его край

3

3. Кольцо (цилиндр) с

ра-

Ось симметрии

2

2

диусами R1 (внутренний) и

m(R1

R2 )

2

R2 (внешний)

4. Сплошной цилиндр

или

Ось симметрии

mR

2

диск радиусом R

2

(R1 = 0, R2 = R)

5. Полый тонкостенный ци-

Ось симметрии

линдр радиусом R, обруч

mR2

(R1 ≈ R2 = R)

6. Сплошной шар радиусом

Ось проходит через центр шара

2mR

2

R

5

36

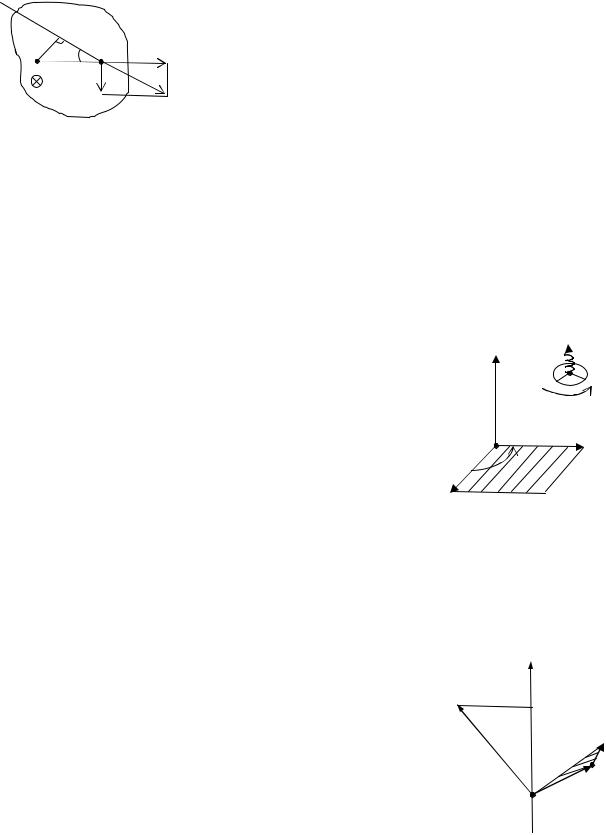
5.2. Момент силы

Рассмотрим тело, которое может вращаться в горизонтальной плоскости относительно оси, проходящей через точку О (рис. 5.3). В точке А к телу приложена горизонталь-

d	r		А	F1	ная сила F . Проведем из точки О в точку А вектор r
О					и разложим силу F на две составляющие: силу F1 ,
M			F2	F	направленную вдоль вектора r , и силу F2 , направ-
	Рис. 5.3				ленную перпендикулярно этому вектору. Из опыта
					известно, что сила F1 не будет вызывать вращатель-
ное движение.				Вращение тела является результатом действия силы F2 . Харак-

теристики вращательного движения (угловые скорость и ускорение) определяются не только величиной силы F2 , но и расстоянием от оси вращения до точки приложения этой силы.

Введем понятие момента силы. Моментом силы F относительно непод-

	вижной точки О (рис. 5.3) называется физическая величина
				M , определяемая
	векторным произведением вектора r на силу F :
				Правый
	M [rF ] .		M
				винт
	Вектор M лежит в плоскости, перпендику-
	лярной плоскости векторов r и F , а его направле-
	ние совпадает с направлением поступательного
	движения правого винта	при его вращении от r к	r	F
	F (рис. 5.4). Модуль момента силы равен
	M rF sin ,		Рис. 5.4
	где α − угол между векторами r и F . Произведе-
	ние r sin d (рис. 5.3) называется плечом силы F		относительно точки О, т.е.

плечо силы − это кратчайшее расстояние от точки О до линии действия силы. Тогда модуль момента силы можно представить как произведение силы на плечо:

M Fd .		z
Единицей момента силы в системе СИ является
ньютон - метр (Н·м).
Моментом силы F относительно неподвиж-	M	M z	F
ной оси z называется скалярная величина Мz, рав-
			r А
ная проекции на эту ось вектора M момента силы,		О
определенного относительно произвольной точки О
данной оси. Значение момента Мz не зависит от вы-
бора положения точки О на оси z (рис. 5.5).		Рис. 5.5
37

5.3. Момент импульса

Моментом импульса (количества движения) L материальной точки А относительно неподвижной точки О называется физическая величина, опреде-

ляемая векторным произведением:						L
	L [rp]		[r ,mV ] ,
где r	− вектор, проведенный из точки О в точку А;
p mV	− импульс материальной точки (рис. 5.6). На-					О
правление вектора L совпадает с направлением посту-									p
пательного движения правого винта				при его вращении		l	r	А
от r к p . Модуль момента импульса равен
	L rpsin rmV sin pl ,						Рис. 5.6
где α − угол между векторами r				и p . Произведение
r sin l называется плечом вектора p относительно точки О.
Моментом импульса относительно неподвиж-
ной оси z называется скалярная величина Lz, равная								z
проекции на эту ось вектора момента импульса L ,
определенного относительно произвольной точки О					L			Lz
данной оси (рис. 5.7). Значение момента импульса Lz									p
не зависит от выбора положения точки О на оси z.
При вращении абсолютно твердого тела вокруг									А
неподвижной оси z, образующей правый винт с на-							О		r
правлением его вращения, каждая отдельная точка
тела движется по окружности постоянного радиуса ri								Рис. 5.7
с некоторой скоростью Vi. Скорость частицы перпен-

дикулярна этому радиусу, т.е. i 90 и sin i 1. Тогда момент импульса от-

дельной частицы относительно оси z можно представить в виде

Liz miVi ri .

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

n

Lz miVi ri . i 1

Учитывая, что Vi ri , где – угловая скорость вращения, получим

n	n
Lz mi ri2	mi ri2 J z ,
i 1	i 1

где Jz – момент инерции тела относительно оси z.

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно этой оси на угловую скорость.

Для однородного тела, симметричного относительно оси вращения, момент импульса относительно любой точки этой оси определяется по формуле:

	(5.1)
L J .

38

5.4. Уравнение динамики вращательного движения твердого тела

Наиболее общая форма записи основного уравнения динамики вращательного движения твердого тела имеет вид

			dL			(5.2)
			dt	M ,
	где		– момент импульса тела относительно неподвижной точки О;			– сум-
		L			M

марный момент всех сил, действующих на тело, определенный относительно той же точки О.

Если твердое тело вращается вокруг неподвижной оси z, то основное уравнение динамики вращательного движения можно записать как

J z M z ,	(5.3)
где J – момент инерции тела относительно оси z; z	– проекция углового уско-

рения на ось z; M z – суммарный момент всех сил, действующих на тело, относительно оси z.

5.5.Закон сохранения момента импульса. Кинетическая энергия вращения

Согласно уравнению (5.2), момент импульса системы материальных точек (тела) может изменяться под действием момента внешних сил. Отсюда следует важный вывод – закон сохранения момента импульса: момент импульса замкнутой системы частиц относительно неподвижной точки О остается постоянным во времени.

Таким образом, если M 0, то

	dL	0	и L const .	(5.4)
	dt

Кинетическая энергия вращательного движения определяется по формуле

T J 2 , (5.5)

вр	2

где J – момент инерции твердого тела относительно оси вращения; – угловая скорость вращения.

39

5.6.Примеры решения задач

1.Вычислить момент инерции тонкого однородного стержня длиной l и массой m относительно оси вращения, проходящей через центр массы (середину стержня).

2

01

2

x

dx

0

x

Дано

Решение

l ;

Момент инерции рассчитываем по формуле J r2dm,

m

m

m

JOO

=?

dx .

1

где r x , dm l

l / 2 m

2

2 m l

3

ml2

В силу симметрии

J

OO1

2

0

l

x

dx

3 l

12

.

2

2. Вычислить момент инерции тонкого однородного стержня длиной l и массой m относительно оси вращения, проходящей через его торец.

	Дано			Решение
	l ;	Зная величину момента инерции стержня относительно оси
	m	вращения, проходящей через его центр масс JC			ml2	, воспользу-
	J =?
					12
		емся теоремой Штейнера:
				2
		l
		J JC m		;
		2

J ml2 ml2 ml2 .

12 4 3

3. Вычислить момент инерции однородного прямоугольного параллелепипеда со сторонами a, b, c и массой m относительно оси z , проходящей через

его центр массы.

Дано		Решение		y				dx
a , b , c ;		Найдем момент инерции			x
				b 2
m		прямоугольного параллелепи-								dy
		педа относительно его геомет-
J z =?				z	r
		рической оси, которая прохо-								y
			a 2							a 2 x
дит через центр основания с длиной сторон a и b
(на рисунке эта ось z перпендикулярна плоско-
					b 2

40