Физика учебное пособие НГТУ

сти рисунка). Пусть две другие координатные оси x и y проходят через центр

основания и параллельны его сторонам.

В силу симметрии момент инерции параллелепипеда J z 4J0 , где J0 –

момент инерции 1/4 части этого параллелепипеда относительно той же оси z . Вычисления проводятся по формуле

J0 r2dm ,

m

где по теореме Пифагора r2 x2 y2 , dm dV cdxdy ( c – высота паралле-

m		m
лепипеда, V			– плотность вещества);
		abc
	a / 2 b / 2																					a / 2 b / 2
J0		x2 y2				ρcdxdy, или J0 ρc																						x2 y2 dxdy.
	0	0																					0		0
Вычисляем интеграл:
			b / 2												b / 2							y	3			b / 2			b x2		b		3
			(x2 y2 )dy x2 y																							0							.
		0													0						3									2	24
Вычисляем интеграл:																				a / 2										a / 2
			a / 2				2		b	3				b x			3									b	3				ba	3		3
				bx																														ab
											dx																		x						.
						2			24					2 3											24						48			48
		0																		0										0
В итоге J0 c	ab(a2 b2 )				,	J z		4 c				ab(a		2 b2 )							.
		48											48

Подставив значение , получаем

J z m(a2 b2 ) .

12

4. Вычислить момент инерции однородного тела массой m с осевой симметрией относительно этой оси, например, момент инерции цилиндра высотой

h с внутренним радиусом R1			и внешним R2	относительно оси
Дано			Решение
R1 , R2 ;		В качестве малого элемента (исходя из dr
m		осевой симметрии) удобно выбрать цилиндр
J =?		с размерами r, dr, h.
		Масса	этого	цилиндра

dm dV hdS h2 rdr . Тогда момент инерции цилиндра

z .

R1

r

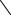R2

41

R2	R2
Jz r2dm 2 h r3dr.
R1	R1

Вычислив интеграл и учтя, что m h (R22 R12 ) , получим окончательно

J z	m(R2	R2 )	.
	1	2
	2

Из этой формулы легко получить момент инерции диска ( R1 0) и бесконечно тонкого кольца ( R1 R2 , R1 R2 ).

5. Вычислить момент инерции сплошного однородного шара массой m и радиусом R относительно оси вращения OO1 , проходящей через его центр мас-

сы.

	Дано		Решение
	R ;
		Разбиваем	шар на	«элементар-
	m
		ные» диски с радиусами r и толщиной
	JZ =?
		dy. Момент инерции		однородного
		«элементарного»	диска	относительно

оси O1O1 dJ r2dm . В силу симметрии рассматри-

2

ваем одну половину шара, момент инерции которой,

					J1/ 2				R r2dm		,
										2
								0
где r2 R2 y2 ; dm dV		m	dV			m			r2dy
		Vшар			4
диска			диска			R		3
					3
значения dm, r2 и произведя вычисления, получаем										J1/ 2
инерции шара J 2J1/ 2 ,

J 2mR5 2 .

y
01 r	dy
R	y
0	x
01

3m3 r2dy . Подставив

4R

mR5 2 . Тогда момент

6. Маховик в форме сплошного диска,	момент инерции которого
J 1,5 кг·м2 , вращаясь равнозамедленно, за время	t 1 мин уменьшил час-

тоту своего вращения с n0 240 об/мин до n1 120 об/мин. Определить: а) угловое ускорение; б) момент Mz сил торможения; в) работу сил торможения A.

42

Дано

Решение

J 1,5 кг·м2 ;

t 1 мин

60 с ;

а. Запишем уравнение динамики вращатель-

ного движения маховика в скалярном виде:

n0 240 об/мин =4 об/с;

J M ,

n1 120 об/мин = 2 об/с

где

t0 t 1

(так как движение равнозамедлен-

=? Mz =? A =?

1

0

ное) или 2 (n0 n1)

. Численно 0,21рад/с2.

t

б. Момент Mz сил торможенияM z

J . Численно Mz

0,31

Н м.

в. Работа сил торможения A T T

T , где

J 2

J 2

T

1

, T

0

.

1

0

1

2

0

2

Угловые скорости

выразим

через

частоты вращения:

1 2 n1 и

0 2 n0 . Окончательно получаем: A 2 2 J (n12 n02 ). Численно A 355 Дж.

7. Вертикально расположенный однородный стержень массой m1 и дли-

ной l может без трения вращаться вокруг своего верхнего конца в вертикальной плоскости. В нижний конец стержня попала, застряв, горизонтально летевшая пуля массой m2 m1 . В результате этого стержень отклонился на угол .

Дано		Найти скорость пули перед ударом.
l ; m1 ; m2 ;		Решение
		Введем обозначения: С – центр масс стержня; h1,2 –
		высота подъема соответственно центра масс стержня и пули,
V =?
		застрявшей в его нижнем конце; V – скорость пули на под-

	лете к стержню; – угловая скорость вращения системы.
I. Запишем закон сохранения момента им-																	z
пульса системы тел (пуля – «стержень – пуля»):
L1z L2z				или lm2V J .										(1)			C
Момент инерции системы «стержень – пу-																	C	h1
ля» относительно оси z подвеса J										m l2	m l		2	.
									1
									3			2				V		h2
Из выражения (1) получаем значение скоро-																m2
сти пули:		J			l	m
									m
V			,	V				1			,			(2)
		m l			m
								3	2
	2				2
где – неизвестная величина.
II. Запишем закон сохранения механической энергии для стержня с за-
стрявшей в нем пулей:							J 2
										m gh m gh .								(3)
								2	1			1		2	2
									43

	Из (3) находим												2g
										2						(m h				m h ) ,				(4)
													J					1	1	2	2
		l			l			l
											2												2
где h							cos		(1	cos ) l sin							, h		l l cos l(1 cos ) 2l sin						.
1		2			2			2							2			2						2
	Подставив h1 и h2									в (4), получаем
										2	2g(m 2m )sin2											/ 2
															1					2			.
															l(m1 / 3 m2 )
	Воспользуемся условием m2 m1 . Тогда
												6g		sin				.
												l						2

III.Скорость V подлета пули определяется выражением (2). Подставив в

(2)значение ω и вновь воспользовавшись условием m2 m1 , получаем значе-

ние

V m1	2gl sin	.
m	3	2
2

8. Через блок цилиндрической формы массой m = 1кг перекинут шнур, к концам которого прикреплены грузы массами m1 = 1 кг и m2 = 2 кг. Найти:

а) ускорение грузов; б) силы натяжения шнура F1 и F2 . Считать шнур невесо-

мым и нерастяжимым. Проскальзывание шнура относительно блока и трение в оси блока отсутствуют.

	Дано		Решение
	m=1 кг;		Так как нить нерастя-
	m1 =1 кг;		жима, путь, пройденный
	m2 = 2 кг		грузом m1 , равен пути,
			пройденному грузом m2 .
	a=? F1=?	F2=?
			Из этого следует, что уско-
			рения грузов одинаковы по

величине a1 a2 a .

Рассмотрим участок нити АБ между грузом m2 и блоком. Уравнение движения этого

участка в проекции на ось y с учетом 3-го закона Ньютона имеет вид mАБa F2 F2 .

Из условия невесомости нити F2 F2 . Аналогично доказывается, что F1 F1 .

М1					ε,	М2
z
					Б
F1					F2
а1		F1 F2 А
					а2
у m1g
			m2g
( mАБ 0 )			следует,			что

Линейная скорость всех отрезков нити в произвольный момент времени t равна V , линейная скорость точек, принадлежащих ободу блока Vбл .

44

Отсутствие скольжения означает, что в любой момент времени V Vбл . Из этого, в свою очередь, следует, что a a R , где R – радиус блока. Тогда

aR .

Система уравнений движения материальных тел в векторной форме: m1a1 m1g F1 ,

m2a2 m2 g F2 ,

		J M F M F .
		2	1
	Запишем уравнения движения обоих грузов в проекции на ось y , а урав-
нение движения блока в проекции на ось z:
Oy:	m1a1 m1g F1 ;	m2a2 m2 g F2 ;
Oz:
	J M z R F2 F1 .

Учитывая приведенное ранее обсуждение условий задачи, а также то, что момент инерции цилиндрического блока J mR2 2 , полученную систему уравнений можно привести к виду

m a m g F ;				m	2	a m	g F ;		ma F F .
1	1	1				2		2	2	2	1
Решая эту систему относительно искомых величин и подставляя числен-
ные значения, получим:
				m2 m1					2
	a g							2,8 м/с ;
			m m m 2
		1				2
		F1 m1 g a 12,6 Н;
		F2 m2 g a 14,0 Н.

9. При горизонтальном положении стержня в руках человека скамья Жу-

ковского и человек вращались с угловой скоростью 1=1,5 рад/с .Момент инер-

ции человекаи скамьиЖуковскогоравен Iчел.+скам=5кг м2, длина стержня lстер =2 м, масса стержня mстер =6 кг. Человек повернул стержень в вертикальное положе-

ние, совпадающее с осью вращения. Найти угловую скорость вращения. В первом положении ось вращения проходит через центр масс стержня.

Дано

1=1,5 рад/с,

Iчел.+скам=5 кг м2, lстер =2 м,

mстер =6 кг

2 = ?

Решение

Согласно условию задачи, момент внешних сил (сил тяжести) относительно оси вращения Z, совпадающей с осью скамьи Жуковского, равен нулю. Следовательно, момент импульса системы «человек+скамья+стержень» относительно этой оси остается постоянным:

45

I1сис 1 I2сис 2 .

(1)

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы. Поэтому момент инерции системы «платформа + человек + +стержень» в первом положении стержня равен

I1сис Iчел скам ml2 / 12 ,

момент инерции системы «платформа+человек+стержень» во втором положении стержня

I2сис Iчел скам .

Подставим в формулу (1) выражения моментов инерции:

( Iчел скам ml2 / 12 ) 1 Iчел скам 2 ,

Откуда

2 ( Iчел скам ml2 / 12 ) 1 Iчел скам .

Произведем вычисления:

2 ( 5 6 22 / 12 ) 1,55 2,1радс.

6. ЭЛЕМЕНТЫ МЕХАНИКИ ЖИДКОСТИ

Жидкость – агрегатное состояние вещества, промежуточное между газообразным и твердым. Из опыта известно, что плотность жидкостей мало зависит от давления, поэтому во многих случаях используют понятие несжимаемой жидкости.

Если в покоящуюся жидкость поместить тонкую пластинку, то части жидкости, находящиеся по разные стороны от нее, будут действовать на каждый ее элемент S с силами F , которые независимо от того, как пластинка ориентирована будут равны по модулю и направлены перпендикулярно площадке S , так как наличие касательных сил привело бы частицы жидкости в движение.

Физическая величина, определяемая нормальной силой, действующей со стороны жидкости на единицу площади, называется давлением Р жидкости:

P FS .

Единица давления – паскаль (Па): 1 Па равен давлению, создаваемому

силой 1 Н, равномерно распределенной по нормальной к ней поверхности площадью 1 м2 (1 Па = 1 Н/м2).

Давление при равновесии жидкостей (газов) подчиняется закону Паскаля: давление в любом месте покоящейся жидкости одинаково по всем направлени-

46

ям, причем давление одинаково передается по всему объему, занятому покоящейся жидкостью.

При поперечном сечении S столба жидкости, его высоте h и плотности вес Fд gSh , а давление на нижнее основание:

Р Fд S gSh S gh ,

т. е. давление изменяется линейно с высотой. При равновесии давление жидкости по горизонтали всегда одинаково. Давление gh называется гидростатиче-

ским давлением.

Сила давления на нижние слои жидкости будет больше, чем на верхние, поэтому на тело, погруженное в жидкость, действует выталкивающая сила, определяемая законом Архимеда: на тело, погруженное в жидкость, действует со стороны этой жидкости направленная вверх выталкивающая сила, равная весу вытесненной телом жидкости:

FА gV .

6.1. Уравнение неразрывности

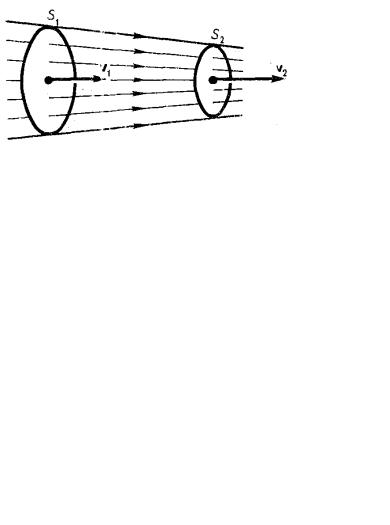
Движение жидкостей называется течением, а совокупность частиц движущейся жидкости – потоком. Графически движение жидкостей изображается с помощью линий тока, касательные к ним совпадают по направлению с вектором скорости. Линии тока проводятся так, чтобы густота их,

характеризуемая отношением числа линий Рис. 6.1 к площади перпендикулярной им площад-

ки, через которую они проходят, была больше там, где больше скорость течения жидкости и меньше там, где жидкость течет медленнее. Таким образом, по картине линий тока можно судить о направлении и модуле скорости в разных точках пространства, т. е. можно определить состояние движения жидкости. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если форма и расположение линий тока, а также значения скоростей в каждой ее точке со временем не изменяются. (рис. 6.1).

Плотность потока – количество жидкости, проходящее через единичную площадку в единицу времени:

j V .

47

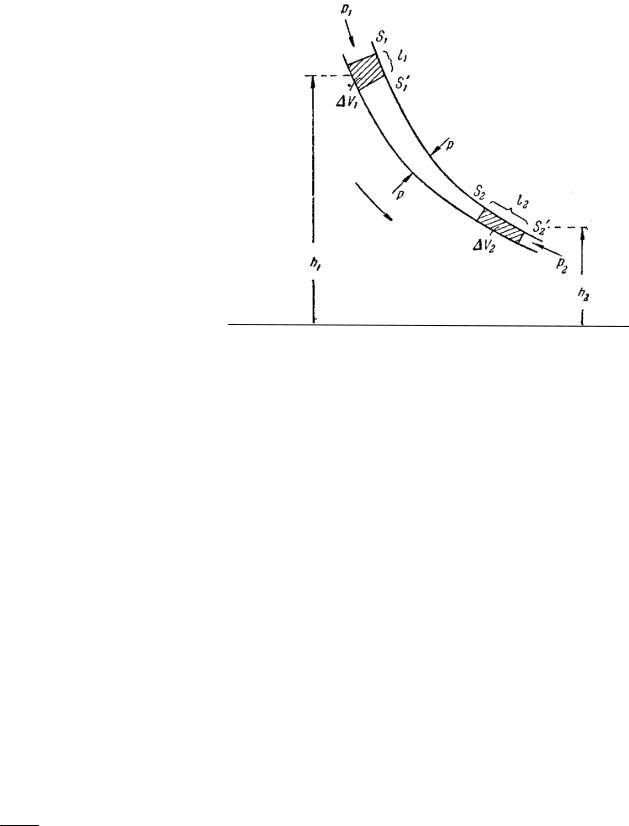
Так как жидкость считаем несжимаемой, то через сечения S1 и S2 за одинаковое время t

пройдут одинаковые объемы жидкости (считаем, что скорость жидкости постоянна), тогда:

j1S1 j2 S2 ,

С учетом формулы для
плотности жидкости	и условия
несжимаемости	жидкости
ρ const , получаем:
V1S1 V2 S2 .
Следовательно, произведе-
ние скорости течения несжимае-
мой жидкости на поперечное се-		П=0
чение трубки тока есть величина			Рис. 6.2
постоянная для данной трубки
тока:
	VS const		(6.1)

Соотношение (6.1) называется уравнением неразрывности для несжимаемой жидкости.

6.2. Уравнение Бернулли

Рассмотрим стационарный поток идеальной жидкости, в которой отсут-

ствует внутреннее трение. Пусть в месте сечения S	известна скорость течения
V , давление Р, высота центра масс рассматриваемых сечений над уровнем,
принятым за нулевой, h (рис. 6.2).
За малый промежуток времени t жидкость перемещается от сечений S1
и S2 к сечениям S1 и S2 , на расстояния l1 V1 t и l2	V2 t .
Согласно закону сохранения энергии:
E2 E1 A ,	(6.2)

где E1 и E2 – полные энергии жидкости массой т в местах сечений S1 и S2 , соответственно, которые складываются из потенциальной ( mgh ) и кинетиче-

ской ( mV2 2 ) составляющих; А – работа, совершаемая при перемещении всей

жидкости, заключенной между рассматриваемыми сечениями, за малый промежуток времени t . Тогда выражение для работы с учетом закона Паскаля примет вид:

A Fl PSl PSV t .

48

Подставляя выражения для работы и полной энергии в формулу (6.2), получим:

mV 2			mV 2
2	mgh		1	mgh P S V t P S V t .							(6.3)
2	2		2	1	1	1	1	2	2	2

Согласно уравнению неразрывности для несжимаемой жидкости (6.1), объем, занимаемый жидкостью, остается постоянным, т. е.

V S1V1 t S2V2 t .

Разделив уравнение (6.3) на V , получим:

V222 gh2 P2 V212 gh1 P1 ,

где – плотность жидкости. Для произвольного сечения получим выражение,

которое называется уравнением Бернулли:

V	2	gh P const.	(6.4)
2

Уравнение Бернулли хорошо выполняется и для реальных жидкостей, внутреннее трение которых не очень велико. Величина Р в формуле (6.4) называется статическим давлением (давление жидкости на поверхность обтекаемо-

го ею тела), величина V2 2 – динамическим давлением. Как уже отмечалось ра-

нее, величина gh представляет собой гидростатическое давление. Для горизонтальной трубки тока ( h1 h2 ) выражение (6.4) примет вид:

				V	2	P const,
		2
где величина	V	2	P называется полным давлением.
	2

6.3. Вязкость (внутреннее трение). Ламинарный и турбулентный режимы течения

Вязкость (внутреннее трение) – это свойство реальных жидкостей оказывать сопротивление перемещению одной части жидкости относительно другой.

При перемещении одних слоев реальной жидкости относительно других возникают силы внутреннего трения, направленные по касательной к поверхности слоев. Действие этих сил проявляется в том, что со стороны слоя, движущегося быстрее, на слой, движущийся медленнее, действует ускоряющая сила. Со стороны же слоя, движущегося медленнее, на слой, движущийся быстрее, действует тормозящая сила.

49

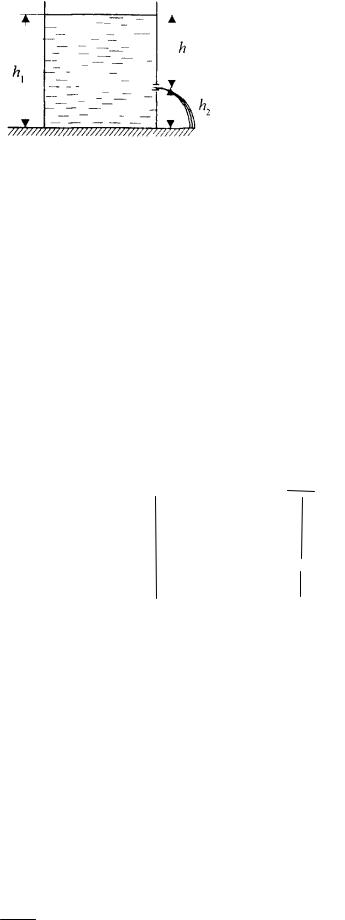
Модуль силы внутреннего трения:

F Vx S ,

где – коэффициент пропорциональности, зависящий от природы жидкости, называется динамической вязкостью; Vx – величина, которая показывает, как

быстро меняется скорость при переходе от слоя к слою в направлении х, перпендикулярном направлению движения слоев, и называется градиентом скоро-

сти.

Существуют два режима течения жидкостей. Ламинарное, при котором линии тока сохраняются вдоль всего потока, каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними. Турбулентное, при котором вдоль потока происходит взаимное перемешивание слоев жидкости и вихреобразование.

6.4.Примеры решения задач

1.Пренебрегая вязкостью жидкости, определите скорость истечения жидкости из малого отверстия в стенке сосуда, если высота h уровня жидкости над отверстием составляет 1,5 м.

Дано								Решение
h=1,5 м		Рассмотрим				два сечения
	трубки		тока: на уровне h1 сво-
V2=?
	бодной поверхности и h2 выхода
из отверстия. Скорость воды на выходе из отверстия
обозначим V2. Считая воду идеальной жидкостью,
запишем для рассматриваемых сечений уравнение
Бернулли, с учетом того, что статические давления
на обоих уровнях одинаковы Р1 Р2					:
		V	2			V	2
		1		gh		2		gh .	(1)
	2		1		2		2

Из уравнения неразрывности:

V1S1 V2 S2 ,

следует, что

V1 V2 S2 ,

S1

где S1 , S2 - площади поперечных сечений бака и отверстия соответственно. Согласно условию задачи, отверстие маленькое, т.е. S1 S2 , поэтому V1 V2

и членом V12 2 в (1) можно пренебречь по сравнению с V22 2. Тогда

gh1 V222 gh2

50