Нач геом

31

A2

B2

x

0

(AB)π1 (AB)π2

B1

A1

Рис. 27.

3.2.2. Следы прямой являются точками, где прямая переходит из одной четверти пространства в другую. Чтобы определить, через какие четверти пространства прямая при своем продолжении проходит, достаточно проанализировать положение ее проекций относительно оси X.

Пример 4. Определить, через какие четверти пространства проходит прямая АВ.

Решение (рис. 28). Сначала строим следы заданной прямой АВП1 и АВП2 . Затем определяем ее положение в пространстве:

на участке левее горизонтального следа прямая проходит в 1 четверти, так как ее проекция А1В1 находится ниже, а проекция А2В2 - выше оси X;

на участке между следами обе ее проекции, а значит и проекции всех точек, находятся ниже оси X - IV четверть;

на участке правее фронтального следа горизонтальная проекция прямой проходит выше, а фронтальная проекция - ниже оси X, следовательно, прямая здесь находится в I четверти пространства.

I	IV	III

A2

B2

x

0

(AB)π1 (AB)π2

B1

A1

Рис. 28.

32

Прямые уровня на той плоскости проекции, которой они параллельны, следа не имеют. На рис. 29 показано построение следов горизонтальной и фронтальной прямых.

Рис. 29.

3.3.Точка на прямой

3.3.1.Точка принадлежит прямой, если ее проекция находится на одноименных проекциях прямой. На рис. 30, а изображен отрезок прямой АВ и точка С, принадлежащая этому отрезку. Если прямая профильная, то принадлежность точки этой прямой может быть установлена с помощью третьей проекции (рис. 30, б). Горизонтальная и фронтальная проекции точки С совпадают с одноименными проекциями прямой АВ, а профильная проекция не совпадает, следовательно, точка С не принадлежит заданной прямой.

3.3.2.Точка на прямой делит отрезок на часта в той же пропорции, в какой ее проекции делят проекции отрезка.

Пример 5. Разделить отрезок АВ на части в соотношении 2:3. Решение (рис. 31). Из точки проводим произвольную прямую и де-

лим ее на 5 равных отрезков. Конечную точку этой прямой соединяем с

точкой В1 и параллельно линии 5– В1 проводим из точки 2 прямую до пересечения с проекцией А1В1. Полученная точка С1 делит проекцию отрезка А1В1 в заданном соотношении, остается построить ее фронтальную проек-

цию С2.

						C2			B2
x	A2										0
					C1					B1
	A1
1				2		3	4		5
				Рис. 31.

33

3.4.Взаимное положение двух прямых

3.4.1.Прямые параллельны, если параллельны их одноименные проекции (рис. 32, а).

а)	б)	в)
	Рис. 32.

Для профильных прямых параллельность может быть установлена с помощью третьей проекции (рис. 32 б, в). На рис. 32, в показано, что прямые АВ и CD в действительности не параллельны. Впрочем, это могло быть установлено и без построения третьей проекции: у прямой АВ обозначение конечных точек на обеих проекциях идет в одном направлении, а у прямой СD - в разных направлениях - это явный признак непараллельности прямых.

3.4.2. Две прямые пересекаются, если их одноименные проекции пересекаются в одной общей точке - проекции этой точки лежат на одном перпендикуляре в оси X.

			B2		C2		z	C3
		C2					B2
									B3
		K2
	A2	D2		A2	D2			A3	D3
x			0	x			0
		D1
	A1				C1
				A1
		K1
		C1			D1	B1
			B1
							y
		а)		Рис. 33.				б)

34

Если одна из пересекающихся прямых является профильной, то их действительное взаимное положение может быть установлено с помощью третьей проекции – фронтальная и профильная проекции точки пересечения должны лежать на одном перпендикуляре к оси Z. На рис. 34, б показано, что прямые АВ и CD в действительности не пересекаются.

Это же можно было установить, не прибегая к третьей проекции, с помощью правила деления отрезка в заданном отношении (пример 5).

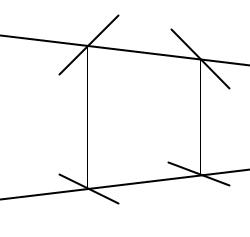
Пример 6. Построить произвольную прямую m, пересекающуюся с двумя заданными прямыми АВ и CD.

Решение (рис. 34). Проводим произвольную фронтальную проекцию прямой m2 и отмечаем точки ее пересечения с заданными прямыми - 12 и 22. Из этих точек проводим вертикальные линии связи и на горизонтальных проекциях заданных прямых находим горизонтальные проекции точек 11 и 21. Через точки 11 и 21 проводим горизонтальную проекцию m1.

Рис. 34.

Пример 7. Построить профильно-проецирующую прямую, пересекающуюся с двумя заданными прямыми (АВ) и (CD).

Решение (рис 35). Как известно, профильно-проецирующая плоскость перпендикулярна к плоскости х3 и ее горизонтальная и фронтальная проекции параллельны оси X. Взять произвольно одну из них мы не можем, так как при этом вторая проекция не будет параллельна оси X. Поэтому возможно только одно единственное решение. Для этого достаточно построить профильные проекции заданных прямых А3В3 и C3D3, точка их пересечения покажет профильную проекцию искомой прямой m3. Теперь положение фронтальной проекции m2 становится определенным, а горизонтальная проекция m1 находится по двум общим точкам 1 и 2.

35

Рис. 35.

Пример 8. Через точку Е провести прямую m, пересекающую две заданные прямые АВ и CD.

Решение (рис. 36). В данном примере прямая АВ перпендикулярна к плоскости х1, следовательно, с ее горизонтальной проекцией в виде точки должна совпадать и точка пересечения с прямой m, поэтому через точку Е мы можем провести горизонтальную проекцию искомой прямой m1. По условию задачи эта прямая должна пересекать и прямую CD - отмечаем точку пересечения 2, находим ее фронтальную проекцию 22, через которую и пройдет фронтальная проекция искомой прямой m2.

Рис. 36.

3.4.3. Если прямые не пересекаются и не параллельны, то они скрещиваются.

36

Одноименные проекции скрещивающихся прямых могут пересекаться, но точки их пересечения не лежат на одном перпендикуляре к оси

X (рис. 37).

m2			n2
12	32		42

22

x					0
				41
	m1
11			21	31
				n1

Рис. 37.

Точка пересечения скрещивающихся прямых в действительности представляет собой совмещенные проекции двух точек, принадлежащих одной и другой из заданных прямых. Такие точки, расположенные на одном перпендикуляре к плоскости проекций, называются конкурирующими.

Если хотя бы одна из скрещивающихся прямых является профильной, то истинное их взаимоположение устанавливается с помощью третьей проекции (рис. 33, б) или по правилу деления отрезка в заданном отношении (пример 5).

3.4.4. Прямой угол проецируется на плоскость без искажения, если хотя бы одна из его сторон параллельна этой плоскости.

Это свойство прямого угла широко используется в начертательной геометрии при решении задач, связанных с построением перпендикуляров.

Пример 9. Из точки С опустить перпендикуляр на прямую АВ. Решение (рис. 38). Заданная прямая АВ есть прямая частного поло-

жения, параллельная плоскости х1. Следовательно, ее можно рассматривать, как одну из сторон прямого угла, на которой прямой угол можно строить без искажения. Из точки С1 проводим прямую, пересекающую проекцию А1В1 под прямым углом в точке К, затем находим фронтальную проекцию перпендикуляра С2К2.

37

Рис. 38.

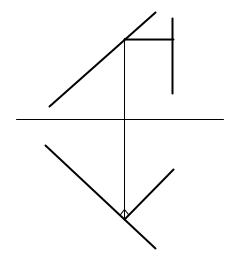
Пример 10. Дана прямая АВ. В точке С восстановить перпендикуляр к прямой АВ длиной 30 мм.

Решение (рис. 39). Прямая АВ есть прямая общего положения, не параллельная ни одной из плоскостей, проекций, следовательно, опустить на нее перпендикуляр без искажения прямого угла нельзя, а вот восстановить перпендикуляр в любой заданной точке можно. Для этого необходимо, чтобы сам перпендикуляр был параллелен какой-либо плоскости проекции, например, плоскости х1. В точке С проводим прямую под прямым углом к А1В1 и откладываем на ней заданную длину перпендикуляра - 30 мм. Затем находим фронтальную проекцию перпендикуляра С2D2, которая по условию задачи должна быть параллельной оси X.

38

Рис. 39.

Пример 11. Провести прямую m, перпендикулярную к двум заданным прямым АВ и CD.

Решение (рис. 40). Из двух заданных прямых одна CD - перпендикулярна к плоскости х1, является прямой частного положения, следовательно, может быть использована для построения прямого угла без искажения, причем любой перпендикуляр к ней будет параллелен плоскости х1. Раз так, то мы можем провести горизонтальную проекцию прямой m1 перпендикулярно к прямой общего положения АВ, то есть m AB. Отметив точки пересечения ее с проекциями А1В1 и C1D1, мы найдем фронтальную проекцию этой прямой.

Рис. 40.

Пример 12. Дана сторона прямоугольника ВС и одна из проекций второй стороны AВ. Достроить проекции прямоугольника АВСD.

Решение (рис. 41). Сторона ВС - горизонтальная прямая, следовательно, вторую проекцию стороны АВ мы можем провести к ней под прямым углом и найти недостающую проекцию точки D. Имея две стороны прямоугольника мы можем достроить проекции всего многоугольника, так как противоположные стороны его параллельны.

39

Рис. 41.

40

ГЛАВА 4 ПРОЕЦИРОВАНИЕ ПЛОСКОСТИ

4.1.Способы задания плоскости на чертеже

4.1.1.Любая плоскость на чертеже может быть задана следующими

способами (рис.42):

Рис. 42.

1 - тремя точками, не лежащими на одной прямой;

2- прямой и точкой, не лежащей на этой прямой;

3- двумя пересекающимися прямыми;

4- двумя параллельными прямыми;

5- плоской фигурой;

6- следами.

Все эти способы равнозначны и легко переводятся один в другой. 4.1.2. Следом плоскости называется линия ее пересечения с плоско-

стью проекции (рис. 43).

Рис. 43.