
- •Нормальное распределение
- •210100 Электроника и наноэлектроника
- •Теоретические сведения
- •Основные термины и определения
- •Понятия о законах распределения одномерных случайных величин
- •Построение гистограммы распределения случайной величины
- •Параметры нормального распределения
- •Проверка гипотезы о согласовании выборочного эмпирического распределения с гипотетически нормальным распределением
- •Практические упражнения
-
Понятия о законах распределения одномерных случайных величин
Вид
(закон) распределения случайной величины
устанавливает связь между возможными
значениями xk
этой случайной величины и соответствующими
вероятностями
 (или плотностями вероятностей
(или плотностями вероятностей
 ) появления данной случайной величины
x
в её генеральной
совокупности. Закон распределения может
быть задан различными способами: в виде
аналитического выражения, графически,
либо в виде таблицы. Форма распределения
случайной величины определяется её
природой.
) появления данной случайной величины
x
в её генеральной
совокупности. Закон распределения может
быть задан различными способами: в виде
аналитического выражения, графически,
либо в виде таблицы. Форма распределения
случайной величины определяется её
природой.
Используют две основные формы выражения закона распределения случайной величины: интегральную и дифференциальную.
Интегральная
функция распределения
 , пример которой приведён на рисунке 1,
для генеральной совокупности или её
оценка
, пример которой приведён на рисунке 1,
для генеральной совокупности или её
оценка
 для выборки показывают, какая доля
статистической совокупности лежит
левее данного конкретного значения xj
случайной величины x
на её числовой оси, т.е. при x
< xj.
Или для примера рисунка 1
для выборки показывают, какая доля
статистической совокупности лежит
левее данного конкретного значения xj
случайной величины x
на её числовой оси, т.е. при x
< xj.
Или для примера рисунка 1
 – вероятность того, что случайная
величина x
примет значение меньше xj.
– вероятность того, что случайная
величина x
примет значение меньше xj.
Для непрерывной случайной величины справедливо
-
F(x) ≥ 0, при x R.
-
F(xl) ≤ F(xj), при l < j.
-
 .
. -
 .
.
Из определения интегральной функции распределения следует, что вероятность P{xj < x < xl} попадания случайной величины x в интервал (xj; xl) может быть определена как
 55\* MERGEFORMAT ()
55\* MERGEFORMAT ()

Рисунок 1 – Пример интегральной функции плотности распределения вероятности
Дифференциальная функция распределения (функция плотности распределения вероятности) (x) есть производная от интегральной функции распределения F(x)
 66\* MERGEFORMAT ()
66\* MERGEFORMAT ()
Пример функции плотности распределения вероятности для графика рисунка 1 представлен на рисунке 2.
Перечислим основные свойства данной функции:
-
(x) ≥ 0, при x R.
-
 .
. -
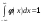 .
.

Рисунок 2 – Пример дифференциальной функции плотности распределения вероятности
Учитывая (5) и (6) можно записать
 . 77\* MERGEFORMAT ()
. 77\* MERGEFORMAT ()
Интервальный
ряд распределения
– это
табличная
(или графическая) форма выражения закона
распределения, т.е. таблица (или график),
где перечислены все k-е
интервалы (k = 1,
2, … , K),
охватывающие возможные(полученные)
значения случайной переменной x,
указаны границы этих интервалов и
приведены вероятности pk
(или плотности вероятностей
 )
появления x
в соответствующих интервалах. При
изучении распределения вместо вероятностей
pk
указывают их оценки:
)
появления x
в соответствующих интервалах. При
изучении распределения вместо вероятностей
pk
указывают их оценки:
 или
или
 .
Другое название интервального ряда –
гистограмма.
.
Другое название интервального ряда –
гистограмма.
-
Построение гистограммы распределения случайной величины
Рекомендуется следующий порядок построения интервального ряда распределения:
-
По данным выборки объёмом N элементов вычисляют среднее значение случайной переменой x:
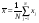 . 88\* MERGEFORMAT ()
. 88\* MERGEFORMAT ()
-
Из элементов выборки находят минимальное xmin и максимальное xmax значения случайной величины x.
-
Оценивают число К интервалов (квантов), на которые надо разделить весь диапазон изменения случайной величины x:
 . 99\* MERGEFORMAT ()
. 99\* MERGEFORMAT ()
-
Оценивают ширину x интервалов:
 1010\* MERGEFORMAT ()
1010\* MERGEFORMAT ()
Полученную величину допустимо округлить до удобного значения.
-
На числовой оси x от величины
 до величин xmax
и xmin строят
интервалы шириной δx,
как показано на рисунке 3. Полученное
количество интервалов К вследствие
выполненных округлений может не
совпадать с расчётным.
до величин xmax
и xmin строят
интервалы шириной δx,
как показано на рисунке 3. Полученное
количество интервалов К вследствие
выполненных округлений может не
совпадать с расчётным.

Рисунок 3 – Построение интервалов по числовой оси случайной величины x
-
Полученные числовые значения границ интервалов (xk-1; xk) заносят в таблицу и подсчитывают число Nk элементов, попавших в каждый k-ый интервал. Элементы, попавшие строго на границу делят пополам между интервалами, разделёнными границей. Если число таких элементов нечётное, то один элемент присваивают интервалу, находящемуся ближе к среднему значению случайной величины, а остальные – поровну между интервалами, разделёнными границей. Также возможно принять одну из границ (например, левую) всех интервалов закрытой, а другую – открытой, и осуществлять подсчёт Nk в соответствии с принятым условием. Числа Nk также заносят в таблицу.
-
Рассчитывают по (1) относительные частоты νk и заносят их в таблицу.
-
Вычисляют оценки
 плотностей вероятностей (плотностей
относительных частот) по (4) и заносят
их в таблицу.
плотностей вероятностей (плотностей
относительных частот) по (4) и заносят
их в таблицу. -
По полученным данным строят графики
 или
или
 либо в виде гистограммы, либо в виде
полигона.
либо в виде гистограммы, либо в виде
полигона.
Форма графиков функций F(x) и (x) определяются природой случайной величины. Некоторые законы распределения случайных величин хорошо изучены в теории вероятностей и математической статистике. Наиболее распространённым и типичным для массовых случайных явлений природы является нормальный закон Гаусса. Известны также законы распределения Пуассона, биноминальный, экспоненциальный и др. Некоторые из них применяются в теории оптимального эксперимента.
Аналитическое выражение кривой (x) нормального распределения Гаусса:
 .
1111\* MERGEFORMAT ()
.
1111\* MERGEFORMAT ()
где M{x} – математическое ожидание случайной величины x; 2{x} – генеральная дисперсия.
