Сопротивление материалов / Ikrin - Soprotivleniye materialov s elementami uprugosti 2004

Примем на втором этапе σ 1r = 0, а σ 2r подберем так, чтобы в процессе роста силы F сохранялось равенство ϕ 3 = 0. С этой целью выполним шаг жордановых преобразований таблицы (а), поменяв

местами ϕ 3 и σ 2r. Придем к таблице (б).

Найдем F2 > F1 , до

1

F /(σ yl A)

σ 1r/σ

yl ϕ 3

=

которого

выбранные

σ 1r

ϕ 1

− 1

0

1

0

≤

0

и σ 2

r

удовлетворяют

усло-

ϕ 2

=

− 1

0

− 1

0

≤

0,

ϕ

вия задачи. Так как,

3 = 0

r

/σ yl =

1

− 1

0

1

,

σ 2

0, (б)

и σ

r

=

0,

то

изменения

ϕ

4

=

− 2

0

0

− 1

≤

1

=

2

0,

функций

ϕ 1,

ϕ 2,

ϕ 4,

... ϕ 8

ϕ 5

− 3

− 3

− 2

≤

описываются

двучленами,

ϕ

=

1

− 2

3

2

≤

0,

6

стоящими

в

соответствую-

ϕ

=

0

− 1

2

1

≤

0,

7

щих строках. Функции, у

ϕ

8

=

− 2

1

− 2

− 1

≤

0.

которых коэффициенты при

F отрицательны, во внимание

не

принимаем – они уменьшаются и

не могут нарушить условия задачи. Из равенств ϕ 5 = 0 и ϕ 8 = 0 соот-

ветственно находим				F = 1,5σ yl A и		F		= 2σ yl A. Принимаем			мень-
шее F 2= 1,5σ ylA.											1r при
	Дальнейший рост силы F обеспечим подбором такого, σ
	1		F /(σ yl A)	ϕ 5	ϕ 3				котором достигшая
									нуля ϕ	останется ну-
ϕ 1	=	− 2	0,667	− 0,333	− 0,667		≤	0,	5
									левой. Для этого ша-
ϕ 2	=	0	− 0,667	0,333	0,667		≤	0,	гом жордановых пре-
σ 2r/σ yl =		1	− 1	0	1		,		образований		табли-
ϕ 4	=	− 2	0	0	− 1		≤	0, (в)	цы (б) меняем мес-
σ 1r/σ yl =		− 1	0,667	− 0,333	− 0,667		,		тами ϕ 5	и σ 1r. Полу-
ϕ 6	=	− 2	0	− 1	0		≤	0,	чаем таблицу (в).
ϕ 7	=	− 2	0,333	− 0,667	− 0,333		≤	0,	С	ростом	силы
ϕ 8	=	0	− 0,333	0,667	0,333		≤	0.	F возрастают ϕ		1 и ϕ 7.

Из равенств ϕ 1 = 0 следует F 3 = 3σ yl A, а из ϕ 7 = 0 F 3 = 6σ yl A. Действительно меньшее.

Дальнейший рост силы невозможен. Во-первых, нет параметров самонапряжений, которыми можно было бы обеспечить его. Вовторых, коэффициенты при ϕ 5 и ϕ 3 в равенствах ϕ 1 и ϕ 7 отрицательны

– допустимые изменения ϕ 5 или ϕ 3 в отрицательную сторону уве-

личат ϕ 1 и ϕ 7. Итак, Fu = F3 = 3σ yl A. Сравнивая его с найденным ранее, видим их совпадение. При F = Fu имеем σ 1r=–0,2σ yl, σ 2r= = 0,1σ yl, что также совпадает с найденными ранее.

Изложенный материал обеспечивает статическую теорему формализованным вычислительным алгоритмом и предоставляет возможность решения задач предельного равновесия, как сформулированных на ее основе, так и методами, построенными на других основаниях.

Отметим роль и смысл параметров самонапряжений. Не следует отождествлять их с действительными остаточными усилиями в конструкции. Остаточные усилия могут быть выражены через параметры самонапряжений, но в общем случае не равны им. Поэтому воспроизводимый расчетом процесс изменения параметров, сопровождающий рост нагрузки, не совпадает с действительным процессом.

Достоинством статического метода является то, что любое приближенное решение системы условий задачи дает значение нагрузки, не превышающее действительную предельную величину. Это открывает широкие возможности для упрощения расчетов и использования различных приближенных методов. Можно ограничиться ка- ким-либо приближенным решением, удовлетворяющим условия статической теоремы, не рискуя допустить погрешность, идущую не в запас прочности.

Расчеты реальных конструкций сводятся к системам, содержащим десятки, сотни, а то и тысячи неравенств. В таких случаях решения возможны только с помощью ЭВМ. В настоящее время разработаны теоретические основы, алгоритмы и стандартные программы решения задач предельного равновесия, что создает благоприятные условия для внедрения статического метода в расчетную практику. Отметим также, что во многих нормативных документах есть рекомендации и требования по расчету строительных конструкций на основе теории предельного равновесия.

400

401

20.3. Кинематический метод расчета упругопластических конструкций

Этот метод опирается на кинематическую теорему теории предельного равновесия. В формулировке теоремы и методе расчета используются новые термины и понятия. Познакомимся с ними.

20.3.1. Кинематически возможные пластические деформации. Механизмы разрушения

20.3.1.1. Пластические деформации, удовлетворяющие условиям совместности, называются кинематически возможными. Так, в шарнирно-стержневой системе (рис. 20.2) условия совместности имеют вид (20.9). Заменив в них полные деформации пластическими,

получим: 3ε 2p = 2ε 1p + ε 4p, 3ε 3p = ε 1p + 2ε 4p. (а)

Это же условие устанавливает кинематическую возможность приращений пластических деформаций:

3∆ε 2p = 2∆ε 1p + ∆ε 4p , 3∆ε 3p = ∆ε 1p + 2∆ε 4p.

(20.28)

Найдем остаточные напряжения, вызванные кинематически возможными пластическими деформациями. Для этого запишем условия (а) в форме

	ε 2p	=	2/3 1/3	ε 1,p
	ε 3p		1/3 2/3	ε 4p

подставим их в равенства (20.14) и перемножим матрицы.

σ 1r		–0,3	0,4	0,1	–0,2	1	0				0 0				0
σ 2r	= E	0,4	–0,7	0,2	0,1	2/3 1/3			ε 1p	=	0 0		ε 1p	=	0
r		0,1	0,2	–0,7	0,4	1/3 2/3			p		0 0		p		0
σ 3									ε 4				ε 1
σ 4r		–0,2	0,1	0,4	–0,3	0	1				0 0				0

Остаточные напряжения, соответствующие кинематически возможным пластическим деформациям, равны нулю. Равенство (б)

справедливо и для приращений пластических деформаций и остаточных напряжений при условии (20.28). Обнаруженное свойство кинематически возможных пластических деформаций проявляется и в более сложных конструкциях.

20.3.1.2. Механизм разрушения – это геометрически изменяемая система, в которую превращается конструкция вследствие текучести некоторых ее элементов. Математическим описанием механизмов разрушения является условие кинематической возможности приращений пластических деформаций. Например, для рассматриваемой шарнирно-стержневой системы условия (20.28) описывают все возможные механизмы (рис. 20.13). Приняв, скажем, ∆ε 4p = 0,

имеем 3∆ε 2p = 2∆ε 1p и 3∆ε 3p = ∆ε	1p (рис. 20.13 а). Если приравнять нулю
∆ε 1p, то соотношения (20.28)	опишут механизм, изображенный на

рис. 20.13 б: 3∆ε 2p = ∆ε 4p, 3∆ε 3p = 2∆ε 4p. Аналогично для ∆ε 3p = 0 следуют соотношения, описывающие механизм, показанный на рис. 20.13 в. Так, перебирая варианты соотношений между приращениями пластических деформаций, можно описать все механизмы.

а)	∆ε 1p<0	б)	∆ε	в)
				4p<0
	∆ε 1p >0		∆ε	4p >0
	На рис. 20.13		Рис. 20.13
		приведены примеры так называемых простых

механизмов. Они характеризуются одним геометрическим парамет-

ром (∆ε 1p на рис. 20.13 а, ∆ε 4p – 20.13 б).

Механизмы, определяемые двумя или бо'льшим числом параметров, называются избыточными. Некоторые из них изображены на рис. 20.14.

∆ε	1p<0, ∆ε 4p<0	∆ε 1p<0, ∆ε 4p >0
∆ε	1p >0, ∆ε 4p >0	∆ε 1p >0, ∆ε 4p<0

Рис. 20.14

В дальнейшем, говоря о механизмах разрушения, будем иметь в виду простые механизмы.

402

20.3.2. Кинематическая теорема теории предельного равновесия.

Алгоритм расчета разрушающей нагрузки кинематическим методом

20.3.2.1. Кинематическая теорема о разрушающей нагрузке мо-

жет быть сформулирована так. Из всех нагрузок, соответствую-

щих различным механизмам разрушения, действительной является наименьшая.

Система математических соотношений задачи в рассматриваемом случае должна содержать описание всех возможных механизмов и условие разрушения. Проиллюстрируем этапы формирования условий задачи примером.

20.3.2.2. Решим кинематическим методом задачу, рассмотренную в разделах 20.1.2 и 20.2.1 (рис. 20.15). Все механизмы разрушения описываются равенствами (20.28). Однако любая комбинация указанных соотношений между приращениями пластических деформаций соответствует двум механизмам. Это показано на рис. 20.13 и 20.14. Чтобы ввести соотношения, отвечающие конкретной геометрически изменяемой системе, преобразуем условия (20.28). Для этого представим приращение каждой пластической деформации

в виде (20.5): ∆εε ip = ∆λ		*2i− 1 – ∆λ	*2i при ∆λ *2i− 1 ≥ 0, ∆λ		*2i ≥ 0, понимая под
∆λ *2i− 1 –	пластическое удлинение,			а под ∆λ *2i	– укорочение	i-го
стержня. Теперь равенства (20.28) можно записать так:
		3(∆λ *3 – ∆λ *4) = 2(∆λ *1 – ∆λ *2) + ∆λ *7 – ∆λ *8;
		3(∆λ	*5 – ∆λ	*6) = ∆λ *1 – ∆λ	*2 + 2(∆λ *7 – ∆λ *8);
∆λ 1	∆λ 3 ∆λ 5 ∆λ	8	∆λ	*m ≥ 0 (m = 1, 2, ... , 8).		(а)
		Условие разрушения запишем в виде
	δ			8	*
F	Рис. 20.15			F δ ≥ Σ1 σ yl Al∆λ m.		(б)

Левая часть неравенства – работа силы F на перемещении δ . Правая

часть – работа внутренних сил (рассеяние энергии) в механизме. Ясен смысл неравенства. Если работа внешней нагрузки превышает работу внутренних сил на рассматриваемых кинематически возможных деформациях, конструкция разрушится. Предельному равновесию отвечает равенство левой и правой частей.

В условие (б) входит произведение двух неизвестных величин Fδ – нелинейное выражение. Учитывая, что δ >> 0, поделим на него

обе части и запишем	F ≥Σ18 σ yl A∆λ m,		(в)
где ∆λ m= l∆λ *m/δ . Наконец, δ = l∆ε		2 = l(∆λ *3 – ∆λ	*4), что равносильно
	1 – ∆λ	3 + ∆λ 4 = 0.	(г)

Задача об определении разрушающей нагрузки свелась к поиску minF при условиях (а) ... (г) и неотрицательных ∆λ m.

	20.3.2.3. Умножим равенства (а) на l/δ										и сведем условия (а), (б),
(в) и (г) в таблицу (д). Каждое ограничение обозначим буквой Y с
соответствующим индексом.
Y1	1		F/(σ yl A)	∆λ	1 ∆λ 2 ∆λ		3 ∆λ 4 ∆λ 5				∆λ 6	∆λ	7 ∆λ 8
	=	0	1	− 1 − 1		− 1		− 1 − 1		− 1 − 1 − 1				≥ 0,
Y2	=	− 1	0	0	0	1		− 1	0		0	0	0	= 0, (д)
Y3	=	0	0	2	− 2	− 3		3	0		0	1	− 1	= 0,
Y4	=	0	0	1	− 1	0		0	− 3	3		2	− 2	= 0.

Структура исходных соотношений кинематического метода характерна тем, что в условия задачи входит лишь одно неравенство, остальные – равенства. Расчетную таблицу будем компоновать так. В первой строке запишем условие разрушения, во второй – связь перемещения с деформациями, далее – условия кинематической возможности. Первый столбец – столбец свободных членов, второй – параметра нагрузки, третий и далее – столбцы, содержащие ∆λ m. Отметим также:

–коэффициенты при ∆λ m в условии разрушения отрицательны;

–свободный член присутствует только во второй строке;

–параметр нагрузки входит с положительным коэффициентом только в условие разрушения.

Для решения задачи необходимо исключить ограничения-

равенства переводом в левую часть таблицы соответствующих ∆λ m – сформировать механизм разрушения. Учитывая специфику структуры системы ограничений и ориентируясь на задачи теории предельного равновесия, в процессе преобразований будем руководствоваться следующими алгоритмом и рекомендациями:

404

1) Разрешающей может быть строка-равенство, которая при стоящих на верху таблицы ∆λ m= 0 противоречит условию задачи;

2)Разрешающим может быть элемент, знак которого противоположен знаку свободного члена;

3)Разрешающим следует принимать элемент, у которого абсолютное значение его отношения к соответствующему коэффициенту первой строки наибольшее;

4)После выбора разрешающего элемента следует выполнить шаг жордановых преобразований таблицы;

5)Столбцы, содержащие переведенные вправо Yj = 0, можно не записывать.

Действия, отвечающие последовательности 1) ... 5), следует вести до тех пор, пока не будут удовлетворены все условия задачи.

В результате выполненных преобразований сформируется окончательная таблица с характерной структурой первых двух столбцов.

В первом столбце

– останется лишь один отрицательный коэффициент первой строки;

–коэффициенты при переведенных влево ∆λ m будут положительными;

–коэффициенты при оставшихся слева Yj (такое может быть при частичном механизме разрушения) – нулевые.

Во втором столбце останется единственный положительный коэффициент первой строки, остальные – нулевые.

Первая строка при оставшихся наверху таблицы ∆λ m= 0 определяет разрушающую нагрузку.

20.3.2.4. Решим задачу (а), … , (г) – табл. (д). Согласно описан-

ному алгоритму меняем местами Y2 с ∆λ									3.
Y1	1		F/(σ yl A)	∆λ	1	∆λ 2 ∆λ		4	∆λ 5	∆λ 6	∆λ	7 ∆λ 8
	=	− 1	1	− 1 − 1			− 2 − 1 − 1 − 1 − 1						≥ 0,
∆λ 3	=	1	0	0		0	1		0	0	0	0	≥ 0,
Y3	=	− 3	0	2		− 2	0		0	0	1	− 1	= 0,
Y4	=	0	0	1		− 1	0		− 3 3		2	− 2	= 0.

Затем Y3 с ∆λ			1.
Y1			1		F/(σ yl A)	∆λ 2	∆λ 4	∆λ 5	∆λ	6	∆λ 7	∆λ 8
		=	− 2,5		1	− 2	− 2	− 1	− 1		− 0,5 − 1,5		≥	0,
∆λ 3 =			1		0	0	1	0	0		0	0	≥ 0,
∆λ	1	=	1,5		0	1	0	0	0		− 0,5	0,5	≥	0,
Y4		=	1,5		0	0	0	− 3	3	1,5 − 1,5			= 0.
Далее Y4 с ∆λ			5.
Y1			1		F/(σ yl A)	∆λ 2	∆λ 4	∆λ 6	∆λ	7	∆λ 8
		=		− 3	1	− 2 − 2 − 2 − 1 − 1						≥	0,
∆λ 3 =				1	0	0	1	0	0		0	≥ 0,
∆λ	1	=		1,5	0	1	0	0	− 0,5		0,5	≥	0,
∆λ	5	=		0,5	0	0	0	− 1	− 0,5		0,5	≥	0.

Условия задачи выполнены. Минимальное значение F, удовлетво-

ряющее первое неравенство Fu		= 3σ yl A. Механизм разрушения
определяется последними	тремя	строчками:	∆λ 1 = 1,5; ∆λ 3 = 1;
∆λ 5 = 0,5. Он изображен на рис. 20.16 а.
а)		б)
∆λ 1 = 1,5 ∆λ 3 = 1 ∆λ	5 = 0,5	∆λ 1 = 2 ∆λ	3 = 1 ∆λ 8 = 1
	Рис. 20.16

Отметим особенность приближенного решения задачи кинематическим методом. Если отказаться от поиска действительного механизма разрушения и задаться каким-либо из них, например, изображенным на рис. 20.16 б, в котором ∆λ 1 = 2, ∆λ 3 = 1, ∆λ 8 =1, то по табл. (д) имеем Fu = 4σ yl A – больше действительного. Любое приближенное решение задачи кинематическим методом дает завышенное значение разрушающей нагрузки. Впрочем, это свойство отражено в самой формулировке теоремы.

406

20.3.3. Примеры расчетов балок кинематическим методом при известных механизмах разрушения

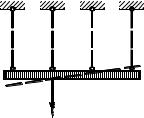
Балки и плоские рамы превращаются в механизмы в результате достижения изгибающими моментами предельных величин в некоторых сечениях. Распределения напряжений в сечениях проиллюстрировано рис. 20.9 и 20.10. Поскольку под расчетными сопротивлениями подразумеваются пределы текучести, все волокна балок деформируются при постоянных напряжениях – текут. Происходит взаимный поворот частей балки, разделенных таким сечением. Появившаяся кинематическая свобода схожа с возможностью, предоставляемой шарнирной связью. Однако эта свобода появляется при достижении моментом предельной величины. В теории предельного равновесия такую кинематическую свободу называют пластическим шарниром. От обычной шарнирной связи он отличается двумя особенностями (рис. 20.8):

–изгибающий момент в нем равен предельному;

–пластический шарнир односторонний – при уменьшении момента он закрывается.

Рассмотрим простейшие примеры балок и нагрузок, при которых механизмы разрушения либо очевидны, либо устанавливаются несложным анализом.

20.3.3.1. На рис. 20.17 а изображена балка, рассчитанная выше

		F		статическим		методом.	Найдем
а)				разрушающее значение силы ме-
		2
				тодом кинематическим.
	1			Балка превратится в меха-
l		l	2l	низм (рис. 20.17 б), когда под си-
				лой (сеч. 1) и над средней опорой
б)	F			(сеч. 2)	откроются пластические
				шарниры.
		θ
		v		Работа силы Wext = Fv.
2θ				Работа внутренних сил
		Рис. 20.17		Wint= Mu2θ + Muθ = 3Muθ .
Но θ = v/l.		Таким	образом, Wint = 3Muv/l.		Из	равенства	работ

Wext = Wint = Fv = 3Muv/l находим Fu= 3Mu/l, что совпадает с полученным ранее статическим методом.

20.3.3.2. В предыдущем примере механизм разрушения был очевиден. Решение задачи предельного равновесия оказалось несложным. В некоторых расчетных схемах механизм качественно ясен, но требует дополнительного анализа. Для иллюстрации ска-

занного рассмотрим балку, изображенную на рис. 20.18 а.
Балка разрушится в результате об-			а)		q
разования пластических шарниров		в
пролете и на правом конце (рис. 20.18 б).					l
Работа внешней нагрузки Wext = ∫0lqvdz =				z
= q ∫0lvdz = 0,5qlδ . Углы поворота в меха-			б) θ 0		v	θ 2
низме θ 0 = δ /z, θ 2 = δ /(l −	z), θ 1 = θ 0 + θ 2 =		θ	1	δ
= δ (1/z + 1/(l− z)). Работа внутренних сил				Рис. 20.18
Wint = Mu(θ 1 + θ 2) = Muδ (1/z + 2/(l −		z)).
Условие предельного	равновесия	Wext = Wint		принимает		вид
0,5qlδ = Muδ (1/z + 2/(l −	z)), откуда q = 2Mu(1/z + 2/(l −				z))/l. Место

образования пролетного шарнира найдем из условия минимума разрушающей нагрузки dq/dz = 0, или 2/(l − z)2 − 1/z2 = 0, что приводит к уравнению z2 + 2lz − l 2 = 0, положительный корень которого z = = 0,414l. Разрушающая нагрузка, соответствующая ему, qu = = 11,657 Mu/l2 . Она совпадает с найденной статическим методом.

20.3.4. Пример расчета плоской рамы перебором возможных механизмов разрушения

Расчетные схемы, в которых механизмы разрушения очевидны или легко определяются, встречаются редко. Чаще приходится рассматривать несколько, а то и все возможные механизмы. Проиллю-

стрируем сказанное примером.			2F
Найдем параметр нагрузки,
	F	3Mu
разрушающей плоскую раму, изо-
		2	3	4
браженную на рис. 20.19.
Возможные механизмы разру-		Mu		Mu	l
шения изображены на рис. 20.20 а,		1		5
б, в. Найдем разрушающую нагруз-
		l	l
ку, соответствующую каждому из
них.			Рис. 20.19

408

409

Первый механизм (рис. 20.20 а). Работа внешней нагрузки Wext = F δ 2.

Углы поворота в пластических шарнирах θ 1= θ 2= θ 4= θ 5= δ 2/l.

Работа внутренних сил Wint = Mu(θ 1 + θ 2 + θ 4 + θ 5) = 4Mu δ 2 /l. Из равенства работ следует Fu1= 4Mu /l.

	2F				2F θ 4			2F θ '4
	δ 2		F	θ 2		δ 2
F	θ 2	θ 5	θ 4	δ 3	θ 3	F	α 23 δ 3	θ 3 θ "4
θ 1	а)			б)		θ 1	в)	θ 5

Рис. 20.20

Второй механизм (рис. 20.20 б). Работа внешней нагрузки Wext = 2F δ 3.

Углы поворота в пластических шарнирах θ 3=θ 2+θ 4; θ 2=θ 4= δ 3/l.

Работа внутренних сил Wint = Mu(θ 2 + θ 4) + 3Mu θ 3 = 8Mu δ 3 /l. Приравнивая работы, находим Fu2= 4Mu /l.

Третий механизм (рис. 20.20 в).

Работа внешней нагрузки Wext = F δ 2 + 2F δ 3. Но δ 2 = δ 3. Таким образом, Wext = 3F δ 3.

Углы поворота в шарнирах: θ 1 = θ "4 = θ 5 = δ 2/l = δ 3/l; α 23 = θ '4 = = δ 3/l; θ 3 = α 23 + θ '4 = 2δ 3/l. Внутренние силы в рассматриваемом механизме разрушения совершают работу

Wint = Mu(θ 1 + θ '4 + θ "4 + θ 5) + 3Muθ 3 = 10Muδ 3/l.

Из равенства работ Fu3 = 3,33Mu /l. Минимальное значение – третье:

Fu= 3,33Mu /l.

В рассмотренной расчетной схеме число возможных механизмов разрушения – три. Расчет оказался несложным. Однако с ростом степени статической неопределимости конструкции и количества сил, действующих на нее, число возможных механизмов быстро растет и проиллюстрированный перебор всех вариантов разрушения становится чрезмерно громоздким. В таких условиях необходим формализованный метод формирования расчетных условий и алгоритм вычисления разрушающей нагрузки.

410

20.3.5. Система условий задачи кинематического метода расчета балок и плоских рам

Остановимся на процедуре формирования расчетных соотношений для балок и плоских рам. Система ограничений задачи включает:

–условия совместности приращений пластических деформаций (кинематической возможности);

–выражений перемещений точек приложения сил через пластические деформации;

–условия разрушения.

20.3.5.1. Порядок формирования условий кинематической возможности приращений пластических деформаций:

1) Выбирают основную систему метода сил и строят эпюры моментов от единичных реакций избыточных связей.

2)Назначают конкретные сечения, в которых могут открыться пластические шарниры с углами поворота θ i.

3)Записывают условия совместности пластических деформа-

	j +
ций	Σ M(i1j) θ i = 0.	(а)
	1

В нем: j – номер избыточной связи; i – номер сечения с пластиче-

ским шарниром; M(i1 j) – изгибающий момент в i-м сечении от Xj = 1; i+ – общее число сечений; j+– степень статической неопределимости конструкции. Равенства (а) справедливы и для приращений углов

	j +	i = 0.
поворота ∆θ	i: Σ M(i1j)∆θ
	1
Так как знаки ∆θ		i могут быть любыми, вводят разности
	∆θ i = ∆λ 2i− 1 – ∆λ 2i при ∆λ m ≥ 0 (m = 1, 2, ... , 2i+).		(б)

После этого условия кинематической возможности принимают вид

j +	(i1j)(∆λ	2i− 1 – ∆λ	2i) = 0 ( j = 1, 2, ... , j +).
Σ M				(20.29)
1

Равенства (20.29) описывают все возможные механизмы разрушения.

20.3.5.2. Условие разрушения запишем в виде Wext ≥ Wint:
k+	i +	2i− 1 + ∆λ 2i),
Σ	Fuk δ k ≥ Σ Mui (∆λ		(в)
1	1

411

где Fuk – разрушающее значение k-й силы; δ k – перемещение точки приложения силы Fk в механизме разрушения; Mui – предельный момент i-го сечения. В состоянии предельного равновесия условие (в) превращается в равенство.

Выразим все внешние силы через один параметр: Fk =HkF, где

Hk – числовой коэффициент. После этого условие (в) принимает вид
	k+	i +
	F Σ Hk δ k ≥ Σ Mui (∆λ 2i− 1 + ∆λ 2i).		(г)
	1	1
С другой стороны, на основании теоремы виртуальных работ
	i	+
	δ k =Σ	M (i1k) ∆θ i (k = 1, 2, ... , k+).	(д)
Здесь M (i1k)	1
	– изгибающий момент в заданной статически неопреде-

лимой конструкции от Fk = 1. Умножив равенство (д) на соответст-

вующие Hk и просуммировав, получаем
k+	k+	i +
Σ Hkδ k = Σ HkΣ M (i1k)∆θ			i.	(е)
1	1	1

Поскольку длина пути, на которой сравниваются работы постоянных

сил, не имеет значения, величины δ k не влияют на условие разруше-

k +

ния. Их можно подобрать так, чтобы	Σ Hkδ k = l, где l – некоторый
	1

геометрический параметр, имеющий размерность длины. Учитывая введенный масштаб, запишем условие разрушения (г) в виде

i +
Fl ≥ Σ1 Mui (∆λ 2i− 1 + ∆λ 2i).	(20.30)

В связь перемещений с приращениями пластических деформаций (е) введем индексы текучести (б) и получим равенство

k+	i +
l – Σ HkΣ M(i1k)		(∆λ	2i− 1 – ∆λ 2i) = 0.	(20.31)
1	1		состоит из j++2	выражений:
Система ограничений	задачи

j+ условий совместности (20.29), равенства (20.31) и неравенства (20.30) при ∆λ m ≥ 0 и F > 0. Требуется найти minF.

20.3.6. Пример расчета балки по формализованному алгоритму

Не всегда можно указать действительный механизм разрушения, перебирать все – громоздко. Нужен формализованный алгоритм расчета. Проиллюстрируем алгоритм, описанный в разд. 20.3.2, примером. Найдем силу Fu, разрушающую балку (рис. 20.21 а).

412

В соответствии с описанной последовательностью составления
условий задачи выбираем основную	а)		F
систему метода сил (рис. 20.21 б).				2
Эпюра моментов от единичной силы		1
приведена на рис. 20.21 в. Появление
		l	l	2l
пластических шарниров возможно в
	б)
сечениях 1 и 2. Условие кинематиче-
ской совместности приращений углов	в)	1
поворота в шарнирах (20.29) имеет вид
l(∆λ 1 – ∆λ 2) + 2l(∆λ 3 – ∆λ 4) = 0. (а)	г)	1		2l
Условие разрушения (20.30) –

Fu l ≥ Mu(∆λ 1 + ∆λ 2 + ∆λ 3 + ∆λ 4). (б)	д)	0,406l		0,188l
Для связи перемещения точки 1 с пла-
стическими деформациями построим	е)		∆λ	4 = 1
эпюру изгибающих моментов от F =1
(рис. 20.21 г, д). Согласно равенству
(20.31) имеем		∆λ	1 = 2

l – 0,406l(∆λ		1 – ∆λ	2) + 0,188l(∆λ				3 –∆λ			4) = 0.					Рис. 20.21						(в)
Решим задачу (а), (б), (в). Сведем условия в таблицу.
Действуя			1	Ful /Mu			∆λ		1		∆λ		2		∆λ	3		∆λ	4
по алгоритму,		Y1 =	0	1				−	1		−		1		−	1		−	1		≥ 0,
описанному в		Y2 =	1	0		−	0,406				0,406				0,188		−	0,188			= 0,
п. 20.3.2.3, по-		Y3 =	0	0				1			−		1		2			−	2		=	0.
следовательно
получаем:						1			Ful /Mu				∆λ	2	∆λ	3		∆λ	4
При Fl/Mu= 3,			Y1	=	− 2,462				1				−	2	− 1,462		−	0,538			≥ 0,
∆λ 2 = ∆λ 3	= 0	все	∆λ 1 =			2,462			0				1		0, 462		−	0,462			≥ 0,
условия	выполне-		Y3	=		2,462			0				0		2,462		−	2,462			= 0.
ны. Так как коэф-													1		Ful /Mu		∆λ		∆λ
фициенты при ∆λ 2 и ∆λ				3 в первой					Y1		=							2		3	≥ 0,
строке отрицательны, Fu = 3Mu/l.												−		3	1		− 2		−	2
Это совпадает с найденными вы-									∆λ	1	=	2			0		1		0		≥ 0,
ше значениями. Механизм разру-									∆λ	4	=	1			0		0		1		≥ 0.
шения описывается равенством ∆λ								4 = 1, ∆λ			1	= 2 (рис. 20.21 е).

413

20.3.7. Пример расчета железобетонной плиты

Теория предельного равновесия применяется при расчетах же-

лезобетонных конструкций – балок, рам и плит. С целью иллюстра-

ции практического приложения кинематического метода приведем

пример оценки несущей способности железобетонной плиты.

Железобетонная плита, защемленная по периметру, подвержена

равномерному давлению p по всей поверхности (рис. 20.22).

p

Исходные данные:

– размер l = 2 м;

θ 15 θ 34

δ

– армирование – две сетки с

θ 26

ячейкой b×b = 10×10 см,

δ

1

l

l

2

– диаметр

проволоки сеток

d = 5 мм;

θ 12

– толщина плиты h = 16 см,

l

рабочая высота сечения h0= 13 см;

b

3

3

–

расчетное

сопротивление

3l

бетона

Rcnc = 8 МПа,

арматуры

b

l

p Rst = 300 МПа.

4

4

Определим давление, разру-

l

шающее плиту.

В нормативной

литера-

θ 56

туре

по

расчету

железобе-

5

6

δ

тонных плит

для

подобных

1,41l

схем

рекомендуют

прини-

θ 56

4

мать механизм разрушения, в

котором

девять

цилиндри-

θ

1,41l

ческих пластических шарни-

ров:

Рис. 20.22

− по периметру 1−

2, 2− 6, 5−

6 и 1− 5;

−

наклонные 1−

3, 2− 3, 4−

5 и 4− 6;

−

посередине плиты 3− 4.

Работа давления на перемещениях механизма Wext = pVw, где

Vw− объем эпюры прогибов. Представив ее двумя пирамидами с ос-

нованиями

2l×l , высотами δ , и трехгранной призмой с ребром 3− 4,

находим Wext = p(2 2l l δ /3 + 2l l δ /2) = 2,33 pδ l 2.

414

Найдем предельные моменты в пластических шарнирах. Рассмотрим, например, шарнир 1− 5 (рис. 20.23). Отсутствие

продольной силы дает равенство Rcncbyo= RstAst. Учитывая, что Ast =

= π d2 /4 = 3,14 0,52/4 = 0,196 см2,			Ast		Rst
находим высоту сжатой зоны бе-					Mu
тона в шарнире yo=RstAst,/(Rcncb) =			h0	h
= 30 0,196/(0,8 10) = 0,74 см. Пре-					Rcnc
			y0
дельный момент Mu = RstAst,(h0 –
– y0/2)/b =30 0,196(13− 0,74/2)/10 =
= 7,43 кН.		b	Рис. 20.23
В наклонных шарнирах ар-
матурные стержни наклонены к
сечению под 45о (рис. 20.24). Рас-			y0
смотрим отрезок, обслуживаемый					Mu
парой стержней сетки. Из равен-			h0	h	Rcnc
ства растягивающей и сжимаю-	Rst
			Rst
щей сил					Rst
Rcnc1,41byo= Rst Ast 0,707 2,	1,41b				Rst
находим yo=RstAst,/(Rcncb)=0,74 см.
					Rcnc
Предельный момент в шарнире
Mu=2RstAst0,707(h0–y0/2)/(1,41b) =		Рис. 20.24			Rst
= RstAst (h0 – y0/2)/b = 7,43 кН.

Равенство предельных моментов во всех шарнирах – следствие одинакового армирования плиты в обоих направлениях.

Углы поворотов θ в пластических шарнирах и параметр механизма δ связаны так (рис. 20.22):

θ12 = θ 56 = δ /l; θ 34 = 2δ /l;

θ13 = θ 23 = θ 45 = θ 46 = 2δ /(1,41l ) = 1,41δ /l ; θ 15 = θ 26 = δ /l.

Работа внутренних сил Wint = Mu(2θ 122l + 2θ 153l + 4θ 131,41l + θ 34l).

Выразив углы	поворота через параметр механизма, получаем
Wint = 20Muδ .	По равенству Wext = Wint находим pu= 8,57Mu/l2 =

= 8,57 7,43/22 = 15,9 кН/м2. Этот результат больше действительного, так как истинный механизм разрушения не известен.

В заключении к разделу, посвященному кинематическому методу, отметим и его достоинство – наглядность, и недостаток – отклонения приближенных решений не в запас прочности.

415

20.4. Заключение к разделу

Статический и кинематический методы можно рассматривать как методы альтернативные. Первый из них опирается на условия, при которых конструкция сохраняет способность воспринимать нагрузку, второй − на условия разрушения. Это различие отразилось и в соотношении нагрузок, удовлетворяющих соответствующим теоремам. Любая нагрузка, отвечающая требованиям статической теоремы, не может быть больше разрушающей. И наоборот, силы, при которых согласно кинематической теореме обязательно произойдет разрушение, естественно, не менее предельных. Действительная разрушающая нагрузка − наибольшая по статическому критерию и наименьшая по кинематическому.

Все рассмотренные методы позволяют решить задачу о несущей способности конструкции при однократном монотонном (однопараметрическом) нагружении. В этом их сходство. В то же время статический и кинематический подходы не дают полной информации об остаточных напряжениях, деформациях и перемещениях в конструкции. Расчет же кинетики деформирования предоставляет больше сведений о напряженно-деформированном состоянии. В этом его отличие и в известной мере достоинство.

Линеаризация всех расчетных соотношений позволила решать задачи методами линейной алгебры. Внутри этого раздела математики статический и кинематический методы приводят задачам линейного программирования. Методом, опирающимся одновременно и на статический, и на кинематический критерии, является расчет кинетики деформирования в процессе монотонного роста параметра нагрузки (подобный описанному в разд. 20.1.2). Он приводит к решению систем неравенств в последовательности, опирающегося на физическую основу. При этом расчет воспроизводит историю изменения всех характеристик напряженно-деформированного состояния – напряжений, деформаций и перемещений. Правда, размерность задачи, определяемая числом переменных, в последнем методе выше. Это − “плата” за больший объем получаемой информации.

416

Заключение к курсу

В процессе изучения курса сопротивления материалов студент познакомится со многими новыми понятиями, явлениями, методами экспериментального и теоретического анализа. Так, содержанием учебника охвачены:

–Объекты: стержневые элементы, изгибаемые пластинки, пластинки, нагруженные в своей плоскости, оболочки.

–Виды расчетов: прочность, жесткость, устойчивость.

–Воздействия: статические, динамические.

–Методы анализа: экспериментальные и теоретические.

–Критерии прочности: напряжение в опасной точке, несущая способность конструкции.

–Виды напряженных состояний: простые (одноосные растяжение и сжатие, чистый сдвиг), сложные.

–Критерии теоретического прогнозирования напряженнодеформированного состояния конструкции: статико-геометричес- кие, энергетические.

–Методическое однообразие формирования технических теорий расчетов различных конструкций: выбор исходных предпосылок, составление системы разрешающих уравнений, преобразование системы к виду, удобному для использования.

–Обычный состав разрешающей системы уравнений: статические, геометрические, физические.

–Математические методы решения задач: точные (методы линейной алгебры, теории дифференциальных уравнений, интегрирования в квадратурах и т.п.), приближенные (численные).

Решения одних задач доведены до формул, включенных в нормы, для других приведены методы решения, третьих обозначены направления возможного анализа. Формулы и методы сопротивления материалов применяются и развиваются в спецдисциплинах.

417

			y	Приложения
			d
				1. Сортамент прокатной стали
	h	x	x
				в соответствии
			(b-d)/4	с ГОСТ 8239-72, 8240-72, 8509-72*
			t	(СТ СЭВ 104-74)
			y	Таблица 1
			b	Двутавры

№		Размеры			Пло-			Справочные величины
					щадь
про-	h	b	d	t	сече-		Jx	Wx	ix	Sx	Jy	Wy	iy
филя					ния
		мм			см2		см4	см3	см	см3	см4	см3	см
10	100	55	4,5	7,2	12,0		198	39,7	4,06	23,0	17,9	6,49	1,22
12	120	64	4,8	7,3	14,7		350	58,4	4,88	33,7	27,9	8,72	1,38
14	140	73	4,9	7,5	17,4		572	81,7	5,73	46,8	41,9	11,5	1,55
16	160	81	5,0	7,8	20,2		873	109	6,57	62,3	58,6	14,5	1,70
18	180	90	5,1	8,1	23,4		1290	143	7,42	81,4	82,6	18,4	1,88
18а	180	100	5,1	8,3	25,4		1430	159	7,51	89,8	114	22,8	2,12
20	200	100	5,2	8,4	26,8		1840	184	8,28	104	115	23,1	2,07
20а	200	110	5,2	8,6	28,9		2030	203	8,37	114	155	28,2	2,32
22	220	110	5,4	8,7	30,6		2550	232	9,13	131	157	28,6	2,27
22а	220	120	5,4	8,9	32,8		2790	254	9,22	143	206	34,3	2,50
24	240	115	5,6	9,5	34,8		3460	289	9,97	163	198	34,5	2,37
24а	240	125	5,6	9,8	37,5		3800	317	10,1	178	260	41,6	2,63
27	270	125	6,0	9,8	40,2		5010	371	11,2	210	260	41,5	2,54
27а	270	135	6,0	10,2	43,2		5500	407	11,3	229	337	50,0	2,80
30	300	135	6,5	10,2	46,5		7080	472	12,3	268	337	49,9	2,69
30а	300	145	6,5	10,7	49,9		7780	518	12,5	292	436	60,1	2,95
33	330	140	7,0	11,2	53,8		9840	597	13,5	339	419	59,9	2,79
36	360	145	7,5	12,3	61,9		13380	743	14,7	423	516	71,1	2,89
40	400	155	8,3	13,0	72,6		19062	953	16,2	545	667	86,1	3,03
45	450	160	9,0	14,2	84,7		27696	1231	18,1	708	808	101	3,09
50	500	170	10,0	15,2	100		39727	1589	19,9	919	1043	123	3,23
55	550	180	11,0	16,5	118		55962	2035	21,8	1181	1356	151	3,39
60	600	190	12,0	17,8	138		76806	2560	23,6	1491	1725	182	3,54

	y z0
d
h x	c	x
	t	(b-d)/2
Таблица 2	y
Швеллеры	b

№		Размеры					Пло-		Справочные величины
							щадь
про-
	h		b	d		t	сече-	Jx	Wx	ix	Sx	Jy	Wy	iy	zo
филя
							ния
			мм				см2	см4	см3	см	см3	см4	см3	см	см
5	50		32	4,4		7,0	6,16	22,8	9,10	1,92	5,59	5,61	2,75	0,95	1,16
6,5	65		36	4,4		7,2	7,51	48,6	15,0	2,54	9,00	8,70	3,68	1,08	1,24
8	80		40	4,5		7,4	8,98	89,4	22,4	3,16	13,3	12,8	4,75	1,19	1,31
10	100		46	4,5		7,6	10,9	174	34,8	3,99	20,4	20,4	6,46	1,37	1,44
12	120		52	4,8		7,8	13,3	304	50,6	4,78	29,6	31,2	8,52	1,53	1,54
14	140		58	4,9		8,1	15,6	491	70,2	5,60	40,8	45,4	11,0	1,70	1,67
14а	140		62	4,9		8,7	17,0	545	77,8	5,66	45,1	57,5	13,3	1,84	1,87
16	160		64	5,0		8,4	18,1	747	93,4	6,42	54,1	63,3	13,8	1,87	1,80
16а	160		68	5,0		9,0	19,5	823	103	6,49	59,4	78,8	16,4	2,01	2,00
18	180		70	5,1		8,7	20,7	1090	121	7,24	69,8	86,0	17,0	2,04	1,94
18а	180		74	5,1		9,3	22,2	1190	132	7,32	76,1	105	20,0	2,18	2,13
20	200		76	5,2		9,0	23,4	1520	152	8,07	87,8	113	20,5	2,20	2,07
20а	200		80	5,2		9,7	25,2	1670	167	8,15	95,9	139	24,2	2,35	2,28
22	220		82	5,4		9,5	26,7	2110	192	8,89	110	151	25,1	2,37	2,21
22а	220		87	5,4		10,2	28,8	2330	212	8,99	121	187	30,0	2,55	2,46
24	240		90	5,6		10,0	30,6	2900	242	9,73	139	208	31,6	2,60	2,42
24а	240		95	5,6		10,7	32,9	3180	265	9,84	151	254	37,2	2,78	2,67
27	270		95	6,0		10,5	35,2	4160	308	10,9	178	262	37,3	2,73	2,47
30	300		100	6,5		11,0	40,5	5810	387	12,0	224	327	43,6	2,84	2,52
33	330		105	7,0		11,7	46,5	7980	484	13,1	281	410	51,8	2,97	2,59
36	360		110	7,5		12,6	53,4	10820	601	14,2	350	513	61,7	3,10	2,68
40	400		115	8,0		13,5	61,5	15220	761	15,7	444	642	73,4	3,23	2,75

418

419