Методичка

Количество аргументов в конституенте или импликанте называют ее рангом. При склеивании ранг результирующей конъюкции, т.е. импликанты уменьшаются на "1".Так в конечном выражении F (A,B,C) для сумматора остаются три импликанты второго ранга.

Говорят, что импликанта накрывает все конституенты, в результате склеивания которых она получена. Процесс многоступенчатого склеивания приводит к импликантам, которые не склеиваются с другими членами. Такие импликанты называют простыми. Простые импликанты с конституентами, не имеющими смежных для склеивания, образуют сокращенную дизъюнктивную нормальную форму (ДНФ) функции.

Однако в некоторых случаях в них могут содержаться лишние импликанты, которые могут быть исключены без изменения значения функции. ДНФ, не содержащая лишних импликант, называется тупиковой ДНФ. Некоторые функции могут иметь несколько тупиковых форм. Тупиковая форма, содержащая наименьшее количество букв - аргументов, называется минимальной ДНФ.

Графические методы минимизации логических функций.

Как известно, любая релейная функция выхода от “n” переменных или логическая функция от “n” переменных может задаваться набором номеров конституент единицы. При этом, если набор номеров выходной функции от “n” переменных содержит номера всех конституент единицы, то такая функция по определению тождественно равна I. Графически такую функцию можно изобразить как гиперкуб от “n” переменных. Количество вершин гиперкуба или количества конституент единицы равно 2n.

Например, для одной переменной можно нарисовать следующее графическое изображение. При таком графическом изображении (рис. 3.1) каждой конституенте единицы сопоставляется одна вершина. Вершины будем называть узлами. Теперь возьмем четыре вершины и на этих вершинах построим квадрат.

x

⌐х

Рис. 3.1 Одномерный гиперкуб

В этом случае каждый узел представляет собой одну из четырех конституент единицы функции от двух переменных x и y и эти вершины соответствуют членам логической функции 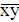, x, , 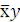xy. На рис. 4.2 эти члены расположены таким образом, что при переходе от любой вершины к соседней, по стороне квадрата изменяется только одна переменная. Если взять сумму

41

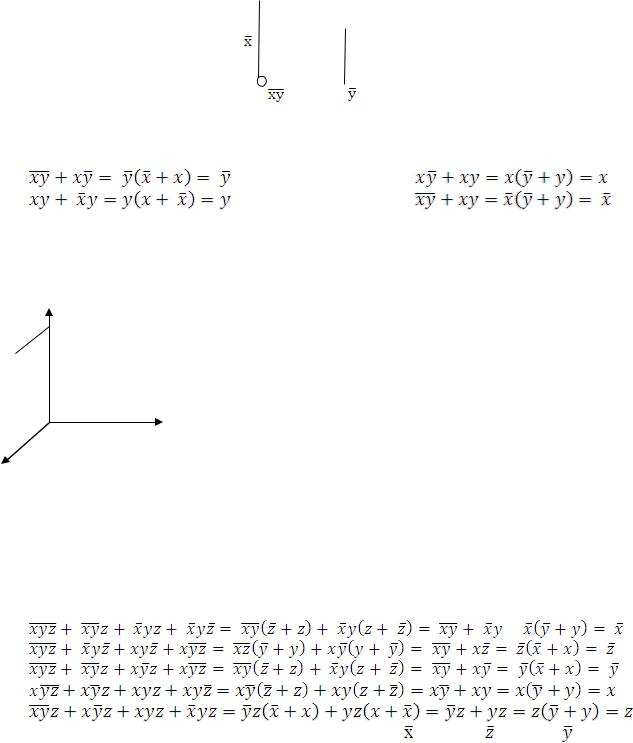
конституент единицы, расположенных на концах любой линии, то всегда одна из переменных будет исключаться.

01		y		11
y				xy
		00	10
			x		x

Рис 3.2 Двумерный гиперкуб

Поэтому эту линию отождествляют с оставшейся переменной. Например, линию, соединяющую углы 10 и 11, можно назвать линией X. Напротив линии x находится линия , а остальные две линии суть линий y и .

	z	001			101		Возьмем 8 узлов, соответствующих восьми возможным
						5	состояниям переменных x, y, z, и на этих узлах построим
			1
011							куб (рис. 3.3). Для всех линий, показанных на рисунке, узлы
					111
							на концах любой линии представляют состояния, которые
			0				отличаются значением только одной переменной.
	2				4	100Следовательно, если сложить члены, соответствующие
		000		6		x	узлам двух концов данной линии, то сложение всегда
	010
					110		приведет к исключению одной переменной.
y
	Рис. 3.3
	Трехмерный
	гиперкуб

Поэтому линия на рисунке соответствует члену, содержащему остальные две переменные. Если сложить члены, находящиеся в вершинах любой грани куба, то это всегда приводит к исключению двух переменных.

=

Каждую из этих граней можно обозначить как – грань, - грань, - грань, x - грань, z – грань, y – грань.

Заданная релейная функция при графическом изображении будет представлять собой ломаную линию, проходящую через узлы, которые являются соответствующими конституентами единицы.

Например, функция заданная набором f = {2, 4, 5, 6} задается ломанной проходящей через узлы 2, 4, 5, 6. Каждая из сплошных линий представляет одну слагаемую релейной функции. Используя свойство, что линии,

42

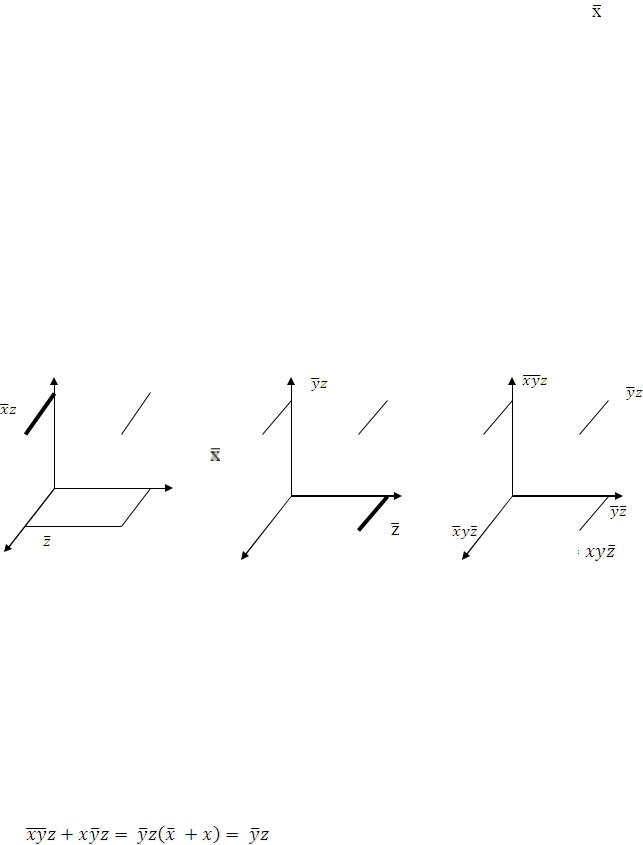
соединяющей два соседних узла, соответствует произведение всех переменных, за исключением той переменной, которая меняет свое значение в концах линии можно записать заданную функцию в следующем виде:

.

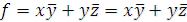Рассматривая рисунок более внимательно, можно заметить, что линия y включает члены 4 и 5 из набора, а линия y включает члены 2 и 6 этого набора. Таким образом, эти две линии включают в себя все члены набора, и любой дальнейший учет этих членов являются лишним. Поэтому линия x, учитывая члены 4 и 6, является избыточной. Таким образом, графическое представление релейной функции позволяет написать ее в таком виде, в котором исключены избыточные переменные и избыточные члены. Данный метод носит название метода Колдуэлла. Колдуэлл предложил геометрическую интерпретацию функции алгебры логики в виде n – мерного гиперкуба. Элементам куба сопоставлены члены различных рангов, вершинам

– члены третьего ранга, ребрам куба члены второго ранга, а граням куба члены первого ранга. Осуществление минимизации (или сокращения) логических функций с помощью гиперкуба рассмотрим на следующем примере.

Пусть задана функция 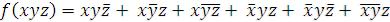Графически эта функция может быть представлена шестью зачернёнными вершинами (рис. 3.6).

z

z

z

x

y

xyz

x

x

x

x

y

x

y

y

y

Рис 3.5

Рис. 3.6

Рис. 3.4

Второй

Третий вариант

вариант

Первый

минимизации

минимизации

вариант

минимизации

В методе Колдуэлла каждый геометрический эквивалент меньшей размерности покрывается всеми геометрическими эквивалентами большей размерности. По аналогии будем говорить о покрытии членов большего ранга соответствующими членами меньшего ранга.

Так, например, члены 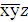и верхних вершин на рис. 3.6 покрываются членом .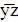

Операция покрытия может быть представлена так:

Для этой операции обычно употребляется термин «склеивание». Для нашего примера возможны два варианта покрытия, соответствующие двум

43

возможным сокращенным формам для данной функции (ребра, соответствующие членам сокращенных форм, на рисунке показаны толстыми линиями).

(рис. 3.4) (рис 3.5)

Эти формы сокращенных функций обычно называют тупиковыми. Их следует сравнить между собой и таким путем найти минимальную форму, т.е. такую, в которой содержится наименьшее число букв. В рассматриваемом случае тупиковых форм оказалось всего две, к тому же примерно равноценных. Количество тупиковых форм резко возрастает с увеличением числа переменных, и описываемый метод становится неэффективен.

Матрицы Карно и применение их для минимизации релейной функции.

Для минимизации релейных функций до 4-х переменных на практике часто пользуются матрицами Карно. Матрица Карно для двух переменных используется в 2х видах. Например, для релейной функции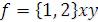

		0 y		1		00				01						11 xy			10
x	0	0		1
								0		1						0				1
	1	1		0
		Рис. 3.7 Матрица Карно для двух переменных
		Таким образом, матрица Карно напоминает диаграмму Вейча: нижний ряд
		клеток отражает области y, а левая колонка - .
		Для трех переменных матрицу Карно можно построить следующим образом.
		Например, для функции									матрица Карно запишется в
		следующем виде:
				z
				0		1								yz
			00	0		0
													00	01		11			10
		xy	01	0		0
											0		0		0		0		0
			11	1		1			x
											1		1		1		1		1
			10	1		1

Рис. 3.8 Матрица Карно для трех переменных

Для четырех переменных матрица Карно для функции f=(0,1,4,6,7,14) xyzw

00 01 11 10

44

имеет следующий вид. Как видно из этих примеров	00	1	1		0	0
матрица Карно построена следующим образом. Со-
седние столбцы и соседние строки соответствуют	01	1	0		1	1
соседним состояниям тех переменных, количество							xy
которых определяет количество столбцов и строк.	11	0	0		0	1
Например, если столбцы или строки предназначены
для изображения одной переменной, то количество	10	0	0		0	0
столбцов или строк будет равно 2.Количество				zw

элементов матрицы Карно равно количеству возможных состояний всех переменных (для 2-х переменных 4, для 3-х переменных 8, для 5 – ти переменных 32, для n переменных 2n).

Матрица Карно заполняется следующим образом. Для заданной релейной функции при помощи набора конституент единицы при известном базисе определяются веса столбцов и строк.

например, задана релейная функция f=(0, 5, 7, 13)xyzw. Так как задан базис(x, y, z, w) определяем вес каждой переменной.

Базис	X	Y	Z	W
Вес	8	4	2	1

переменных

Выберем что столбцы должны соответствовать набору zw,а строки xy

Переменные				ZW
			00		01	11	10
			0		1	3	2
XY	00	0	1		0	0	0
	01	4	0		1	1	0
	11	12	0		1	0	0
	10	8	0		0	0	0

Удобство обращения и экономия времени при использовании матриц Карно во многом зависят от нашей способности распознавать определенные конфигурации ее заполнения. Эти конфигурации носят название "подкубов". Подкуб можно определить как набор клеток матрицы, в котором одно или большее число переменных имеют постоянное значение. В матрице, соответствующей функции четырех переменных, подкуб, состоящий из двух клеток, соседних по горизонтали или вертикали, характеризуется тем, что три переменных в нем постоянны, а четвертая принимает оба своих значения. У подкуба, состоящего из четырех клеток, каждая из которых является соседней относительно двух других, две переменные будут постоянными, в то время как другие две переменные принимают все четыре возможные комбинации значений. Наконец у подкуба, состоящего из 8 клеток, таких что, каждая является соседней относительно трех других в том же наборе, одна переменная будет постоянной, а три другие принимают все восемь возможных комбинаций значений. Таким образом, двух клеточный набор

45

		исключает одну переменную, четырехклеточный - две, а восьмиклеточный -
		три переменные.
			Рассмотрим примеры:
		zw							zw								zw						zw
00		01		11	10		00		01		11	10			00	01			11	10	00		01		11		10
00							00		1		1			00							00						1
xy 01							01							01	1					1	xy
													xy								01
							11							11
11				1																	11
							10							10
10				1																	10						1
		1) 1111							2) 0001							3) 0100					4) 0010
		1011					0011								0110						1010

1- 11 00-1 01 – 0 -010 x-zw

1)

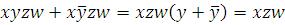
2)

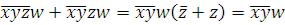
3)

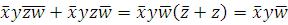
4)

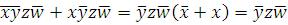
Необходимо отметить одну особенность карт Карно: соседними клетками в одном ряду являются крайняя левая и крайняя правая, соседними в одном столбце являются крайняя верхняя и крайняя нижняя. Поэтому карта Карно представляет из себя развертку цилиндра, разрезанного вдоль горизантальной или вертикальной оси. Кроме того, все четыре клетки являются смежными и могут образовать подкуб.

Введем понятие минимальной импликанты подкуба и определим последовательность минимизации при помощи таблицы Карно.

Минимальной импликантой подкуба назовем произведение букв, остающихся постоянными в этом подкубе. Например, подкуб, показанный

	ниже можно представить импликантой													, .							zw
				yz									00			00 01 11								10
00			01	11		10
																1
	1		1				1			0	x	0	01
																							1	1		yz
	1		1				1
										1			11										1	1
													10					1

Минимизация релейной функции при помощи карты Карно сводится к следующему:

1.Выделяются все подкубы, содержащиеся в заданной релейной функции;

46

2. Выбирается минимальное количество подкубов, покрывающих заданную релейную функцию, и составляется минимальная релейная

функция, которая равна сумме выбранных импликант.												zw
Пример 1: минимизировать релейную функцию		00								01				11			10
			00				0					1			0			0
Как видно из таблицы релейная функция покры-		01
							0					1		1				0
вается тремя подкубами, которым соответствуют		xy
		11
							1				1			1			1
импликанты	. Минимальная релейная
		10					0			0				0			0
функция будет равна:

	00							10		zw
				01			11
00	1			1				1
01	1							1
											xy
11		1		1			1	1
10
		1		1

Пример 2. Минимизировать релейную функцию

.

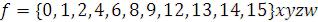Как видно из таблицы, заданную релейную функцию покрывают четыре подкуба ,

но из таблицы видно, что 3 подкуба полностью покрывают заданную релейную функцию.

Предпоследний пример позволяет показать, что картами Карно можно минимизировать логические функции не только в классе ДНФ, но и в классе КНФ. Так как логическая функция полностью определена, то оставшиеся клетки считаются заполненными 0.

Применим к этой же функции метод группирования нулей. Следовательно минимальная форма для отрицания функции имеет вид

Взяв отрицание от 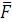и, применив теорему де Моргана, получим минимальную форму в виде

Впрочем, эту же формулу можно получить непосредственно из карты Карно, если считывать «нулевые» кубы в соответствии с правилом, что клетки, образующие S – куб, дают макстерм (n - S) ранга (или имплиценту), в который входят те (n - S) переменные, которые сохраняют одинаковые значения на этом S кубе, причем, значениям 0 соответствуют сами переменные, а значениями 1 – их отрицания. Переменные, которые изменяют свои значения на S кубе, в макстерме отсутствуют. Минимизация в классе КНФ облегчает реализацию логических функций в базисе Вебба.

Интервалы и покрытия. Метод Квайна – Мак – Класки.

Теоретико – множественная интерпретация булевой алгебры оказывается очень удобным языком для изучения ДНФ и построения методов их упрощения. Рассмотрим кратко основные понятия, связанные с ДНФ.

Если функция f(x1, …, xn) представляется элементарной конъюнкцией всех «n» переменных, то Mf (множество единичных наборов функций f) содержит

47

ровно один элемент. Если же f – элементарная конъюнкция k переменных, где k<n, то Mf содержит 2n-k двоичных наборов (т.к. n – k переменных, не вошедших в эту конъюнкцию, несущественны для f и могут принимать любые 2n-k значений, не изменяя f). Множество Mf такой функции f называется интервалом. Например, для

n = 4 и f(x1, x2, x3, x4) = x2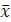4

Mf = {0100, 0110, 1100, 1110} и |Mf| = 22= 4.

В этом случае говорят, что конъюнкция x2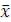4 (тоже интервал M x24) покрывает множество Mf (и все его подмножества). Представление f в виде ДНФ соответствует представлению его единичного множества в виде объединения интервалов; в совокупности все конъюнкции ДНФ покрывают все единое множество f, в частности, СДНФ функции f соответствует просто перечислению элементов Mf. Отношение покрытия между конъюнкциями ДНФ и элементами Mf наглядно задается таблицей покрытия, строки которой соответствуют конъюнкциям (т.е. интервалам), столбцыэлементам Mf ,а на пересечении строки i со столбцом J стоит какая-либо отметка (например I),если i-я конъюнкция покрывает J-й элемент Mf, где Mf - множество единичных наборов функции f.

Например, ДНФ 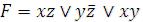соответствует таблица покрытия (таблица 3.6). Из таблицы видно, что исключение xy из F не изменит единичного множества данной функции и получится теоретико-множественное доказательство соотношения обобщенного склеивания:

.

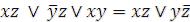Таблица 3.6

	010	101	110	111
xz		1		1
y	1		1
xy			1	1

Эта формула доказывается с помощью развертывания, т.е. с применением

формулы склеивания	в обратную сторону и поглощения
x xy = x т.е.	.

Еще более очевидное обоснование имеет закон поглощения x xy = x.Интервал Mxy всегда покрывается интервалом Mx. Этот закон в терминах ДНФ можно сформулировать следующим образом: любой импликант k ДНФ, не являющийся простым, можно заменить простым импликантом ki, покрывающим k; импликант ki получается из k вычеркиванием некоторых букв.

Методы упрощения ДНФ (а их известно довольно много) состоят, как правило, из двух этапов. На первом этапе получают список всех простых импликант, т.е. сокращенную ДНФ. Это можно сделать, например, при помощи эквивалентных преобразований. На втором этапе, используя таблицу

48

покрытия (или аналогичные методы), удаляют "лишние" импликанты, покрываемые другими импликантами.

ДНФ, из которой нельзя удалить ни одного импликанта, называется тупиковой. Тупиковых ДНФ может быть несколько для одной и той же булевой функции. Импликанта называется обязательной или существенной, если найдется конституента, принадлежащая только ей. Множество обязательных импликант (экстремалей) образуют ядро покрытия, если множество экстремалей не образуют покрытия, то оно дополняется до покрытия другими импликантами .

Для иллюстрации рассмотрим метод Квайна – Мак - Класки. Пусть f={2,5,6,7}.Разбиваем множество конституент I на классы, в каждом из которых содержатся конституенты с одинаковым числом единиц (или нулей) и упорядочим эти классы по возрастающему числу единиц, в которых на одну больше или меньше, то можно ограничиться попарным сравнением соседних классов. Учтенные члены отмечаем знаком "v".

1 шаг	2 шаг		3 шаг
i = 1 010 (2)	i = 1 -10	(2, 6)
i = 2 101 (5)	i = 1-1	(5, 7)	xz
110 (6)	11 -	(6, 7)	xy
i = 3 111 (7)

Сравнение членов между соседними по индексу группами должно быть полным, т.е. каждый с каждым, при этом номера объединенных членов пишут в скобках. Прочерк означает, что данный разряд (переменная) отсутствует. Если дальнейшее объединение невозможно, то все неотмеченные члены во всех столбцах являются импликантами. Далее пишут алгебраическое выражение простой импликанты на основе каждого неотмеченного члена. Завершением работы является построение таблицы покрытия и исключение несущественных импликант, которые покрываются другими.

3.9Вопросы для самопроверки

1.Составьте таблицы истинности для формул:

а)	(x y) (x y)						б)
в)	(x1 x 2 ) x 3 (x 2					x1 )	г)

д) ((x y) (y z)) (x z)

x y (x y) (x y) (x y)

x	y		x y	x y
		x				x y		(x y) (x y)
0	0	1	0	0		1		1
0	1	1	1	0		1		1
1	0	0	1	0		1		1
1	1	0	1	1		0		1

49

2. Установите с помощью таблиц истинности, какие из следующих формул - тавтологии:

	а) x y (x y)																						б) x y (x y)
	в) (x y) (y x)																						г) (x y) (x y)
	д) (x y) (y x)																						е) ((x y) (y z)) (y x)
	3. На основании каких законов логики получены следующие соотношения?
	Докажите их с помощью таблиц истинности :
	x		x		; x x x ; y y y ; x x 1 ; x x 0 ; 0 x 1; x 1 1; x y y x ;
	x y x y ;									x y x y ; x y y x ; x y x y ; x y (x y)(y x)
	4. Какие из данных формул равносильны:
	а) x y								б) x y									в) x y										г) x y
	д) x y								е) y x									ж) x y										з) y x
	5. Полиция задержала 4 гангстеров, подозреваемых в краже автомобиля:
	Анри, Луи, Жоржа и Тома. При допросе они дали следующие показания:
	Анри: «Это был Луи», Луи: «Это сделал Том», Жорж: «Это не я», Том: «Луи
	лжет, говоря, что это я». Дополнительное расследование показало, что правду
	сказал только один из них. Кто украл машину?
					Таблица к задаче 6
																6. Составьте формулы, соответствующие данной таблице
х	y				z			F1					F2
																истинности (выберите рациональный способ). Упростите
0	0			0				1					1
																полученные формулы и изобразите их в виде контактных
0	0			1				0					0
																схем.
0	1			0				0					1			7. Для каждой из данных формул найдите ее СДНФ и
0	1			1				0					1			СКНФ:
1	0			0				1					0			а) x y												б) x y											в) (x y) xz
1	0			1				1					1			г) (x y)(y z) (x y)
1	1			0				0					0			8. Напишите СДНФ представляющую: а) тавтологии с
1	1			1				0					1			переменными х и у; б) тавтологии с переменными х, у и
																а; в) тождественно ложные формулы с переменными х, у
	и а.
	Пример: xy xy xy xy .

9.Составьте всевозможные таблицы истинности для формул с 2 переменными х и у. Выпишите СДНФ и СКНФ формул, соответствующих этим таблицам. Укажите 16 таких таблиц.

10.Один логик попал в плен дикарям в пещеру, имеющую 2 выхода. Вождь дикарей предложил логику следующий шанс на спасение: «Один выход ведет на свободу, другой на смерть. Сделать выбор тебе помогут два моих воина, одному из которых ты можешь задать единственный вопрос. Но предупреждаю тебя, что один из этих воинов всегда говорит правду, а другой всегда лжет». Что должен спросить логик?

11.Установите, какие из данных формул являются ДНФ, СДНФ, КНФ и СКНФ с переменными х, у и z:

а) xy xz

б) xyz xyz

в) (x y)(x z)

50