Методичка

дизъюнктов будет пустой дизъюнкт. Таким образом, выводом пустого дизъюнкта из множества дизъюнктов S называется конечная последовательность дизъюнктов С1, С2, ..., Ск такая, что любой Сi, является или дизъюнктом из S или резольвентой, полученной принципом резолюции.

Вывод пустого дизъюнкта может быть наглядно представлен с помощью дерева вывода, вершинами которого являются или исходные дизъюнкты или резольвенты, а корнем — пустой дизъюнкт.

Пример. Пусть .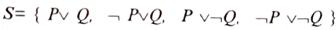

Пронумеруем исходные дизъюнкты:

Вывод представлен на рисунке 6.1с помощью дерева вывода.

Рис.6.1 Дерево вывода

Правило резолюции для исчисления предикатов.

Другими словами, при применении правила резолюции нужны контрарные литералы в резольвируемых предложениях. Пусть С1 и С2 - два предложения в исчислении предикатов. Правило вывода

C1 ,C2 R

(C1' C2' )

называется правилом резолюции в исчислении предикатов, если в предложениях С1 и С2 существуют унифицируемые контрарные литералы P1 и P1, то есть C1 = P1 C1' и C2 = P1 C2' , причем атомарные формулы P1 иP1 являются унифицируемыми наиболее общим унификатором .В этом

случае резольвентой предложений C1 и C2 является предложение ( C1' C2' ), полученное из предложения C1 C2, т.е. ResP1(C1,C2)= ( C1' C2' ) .

81

Опровержение методом резолюций.

Опровержение методом резолюций – это алгоритм автоматического доказательства теорем в прикладном исчислении предикатов, который сводится к следующему. Пусть нужно установить выводимость

S├ G.

Каждая формула множества S и формула G (отрицание целевой теоремы) независимо преобразуются в множества предложений. В полученном совокупном множестве предложений C отыскиваются резольвируемые предложения, к ним применяется правило резолюций и резольвента добавляется в множество до тех пор, пока не будет получено пустое предложение. При этом возможны три случая:

Среди текущего множества предложений нет резольвируемых. Это означает, что теорема опровергнута, то есть формула G не выводима из множества формул S.

В результате очередного применения правила резолюции получено пустое предложение. Это означает, что теорема доказана. то есть S├ G.

Процесс не заканчивается, то есть множество предложений пополняется все новыми резольвентами, среди которых нет пустых. Это ничего не означает.

6.4 Принцип логического программирования.

В первом приближении логическое программирование — это использование дедуктивных процедур (процедур логического вывода) как механизма вычислений. Языки логического программирования являются декларативными в отличие от обычных “процедурных языков”. В них в виде логических аксиом формулируются сведения о задаче и предположения, достаточные для ее решения. Сама задача формулируется как целевое утверждение, подлежащее доказательству. Таким образом, программа представляет собой множество аксиом, а вычисление — это конструктивный вывод целевого утверждения из программы. В логическом программировании (мы будем говорить о языке ПРОЛОГ) используется только одно правило вывода — резолюция.

Резолюция обладает важными свойствами — корректностью и полнотой. Резолюция корректна в том смысле, что если с се помощью из множества формул S = {F1.....Fk} и отрицания формулы R выводится пустой

дизъюнкт, то справедливо 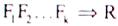. Резолюция является полной в том смысле, что если R является логическим следствием множества формул S, то

пустой дизъюнкт обязательно выводится из 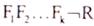. Однако в 1936 году Черчем и Тьюрингом было доказано, что для логики предикатов не существует разрешающего алгоритма для проверки общезначимости (и,

82

следовательно, невыполнимости) формул. Поэтому, запустив процесс логического вывода, в общем случае мы не можем быть уверены в том, что он завершится. Если R не является логическим следствием формул S, то алгоритм доказательства может никогда не завершиться при существовании бесконечного числа возможных резольвент, последовательно получаемых в процессе выполнения алгоритма доказательства.

Однако для предикатов с конечной областью определения, и тем более в логике высказываний, не только положительный, но и отрицательный ответ на вопрос о невыполнимости логической функции всегда будет получен методом резолюции в конечное время (за конечное число шагов).

Логический вывод в ПРОЛОГЕ

Логика предикатов и понятие логического вывода были разработаны в первой половине нашего века, но только в конце 60-х стали понятны огромные возможности логического вывода для

построения непроцедурных алгоритмов; тогда же и были разработаны методы резолюции, алгоритм унификации и, в конце концов, язык логического программирования ПРОЛОГ. Основной вклад в логическое программирование был сделан Аланом Робинсоном (Alan Robinson), Аланом Колмерауером (Alain Colmeraurer) и Робертом Ковальски (Robert Kowalski),

причем он был сделан сравнительно недавно. В этом языке исходное множество формул, для которого ищется пустая резольвента, представляется в виде так называемых “дизъюнктов Хорна”. Хорновские дизъюнкты — это формулы одного из трех типов:

отрицание: факт: А

импликация (правило): А <=(В1, ..., Вm),

где А, В1, ... — литеры — атомные высказывания или предикаты с отрицаниями или без них в нормальной предваренной форме только с (подразумеваемыми) кванторами всеобщности для всех переменных. Очевидно, что любую логическую формулу можно привести к конъюнкции дизъюнктов Хорна. Действительно, факты можно рассматривать как импликации, не имеющие посылок (антецедентов). Отрицания — как импликации, не имеющие следствий (консеквентов). Поэтому все дизъюнкты Хорна - это формулы вида А <= (В1,..., Вm ), которые просто являются другой записью импликации В1&...&Вm => А, и знак <= может читаться как «при условии, что». Итак, все эти формулы представляются в виде дизъюнктов:

или, что то же, в конъюнктивной нормальной форме.

83

6.5Формы представления логических формул.

Клаузальные формы.

Вцелях формализации доказательства выводимости в предыдущих разделах были рассмотрены преобразования правильно построенных формул

впредваренную нормальную форму (кванторы находятся в передней части формул). Предваренная нормальная форма преобразовывалась в нормальную сколемовскю форму исключением кванторов существования и введением специальным образом скулемовских функций и констант.

Вискусственном интеллекте часто бывает полезно представлять формулы в клаузалъной форме. Скулемовская нормальная форма может быть преобразована в клаузальную форму, т. е. в виде множества дизъюнктов. Это позволяет иногда упростить доказательство теорем.

Общий вид дизъюнкта таков:

Дизъюнкт без переменных называется конкретизированным дизъюнктом. Приведенный выше дизъюнкт можно записать в эквивалентной форме:

В зависимости от числа литер в антецеденте (посылке) и в консеквенте (заключении) этой импликации имеем различные по выразительности подмножества языка: логический эквивалент языка реляционных баз данных, логический язык, используемый в Прологе и др.

Когда п позитивных литералов в дизъюнкте строго больше 1, то имеем дело с дизъюнктивной информацией (возможно, условной). В частности, при

m=0 и п>1 дизъюнкт содержи: только позитивные литеры: . С помощью таких дизъюнктов можно представлять неполные сведения. Например, дизъюнкт Рисует (Миша)vРисует(Петя) можно интерпретировать так: "хотя бы один из мальчиков Миша или Петя рисует", но не уточняется, рисует только Миша, рисует ли только Петя или оба мальчика рисуют.

Если т>1 и n>1, дизъюнкт имеет самый общий вид и представляет условную дизъюнктивную информацию. Наличие такой дизъюнктивной информации позволяет выражать неполные знания о мире. Однако формализовать рассуждения на основе таких знаний очень трудно. Поэтому в языках логического программирования, простых дедуктивных базах данных не используют такие дизъюнкты.

Хорновские дизъюнкты

В языках логического программирования, подобных Прологу, ограничиваются хорновскими дизъюнктами,т.е. дизъюнктами, содержащими не более одного позитивного литерала. При m>1 и n= 1 дизъюнкт называется

точным хорновским дизэюнктом, который имеет вид:

84

Р1 … Рm Q, что эквивалентно формуле

Такой дизъюнкт осуществляет представление условной информации и может выступать в качестве правила в Пролог-программе. Точный дизъюнкт выражает некоторое правило: негативные литеры соответствуют гипотезам, а позитивная литера - заключению.

Если антецедент приведенной импликации не содержит литералов (m=0), то, очевидно, имеем дело с безусловной информацией. Такой дизъюнкт называется унитарным позитивным дизъюнктом. Возможны два случая.

•Литерал Q не содержит переменных. Тогда он представляет один конкретизированный литерал, например: Рисует (Миша). Такой дизъюнкт называется фактом. Так выражаются факты в Пролог-программах.

•Литерал Q содержит переменные. Тогда он представляет более общую информацию о термах (переменные рассматриваются универсально квантифицированнми).

Негативные хорновские дизъюнкты.

Дизъюнкт, не содержащий ни одного позитивного литерала, называется негативным. Если в таком дизъюнкте один негативный литерал Р. то он представляет элементарную негативную информацию. Возможны два случая:

•Негативный литерал не содержит переменных. В этом случае он представляет собой элементарный негативный факт. Например,

Рисует (Миша).

•Негативный литерал содержит переменные. В этом случае он представляет негативную информацию обо всех индивидных константах. В базах данных такой литерал должен обрабатываться как ограничение целостности.

Дизъюнкт, содержащий более одного негативного литерала, отражает более сложную негативную информацию. Например, -(Летает(х) Ползает(х)). Интерпретация этого дизъюнкта такова: "ни один объект не может быть одновременно и летающим и ползающим".

В логическом программировании негативный хорновский дизъюнкт представляется в виде вопроса, задаваемого системе вывода.

6.6Вопросы для самопроверки.

1)Что такое исчисление предикатов?

2)Дать основные понятия исчисления предикатов.

3)Какая переменная называется квантифицированной?

4)Из каких компонент состоит исчисление предикатов?

5)Что такое синтаксис исчисления предикатов?

6)Что такое семантика исчисления предикатов?

85

7) В чем заключается метод резолюции в логике высказываний и в логике предикатов?

8) Чем отличается логика высказываний от логики предикатов?

9)Дать основные аксиомы исчисления предикатов.

10)Дать основные правила вывода исчисления предикатов.

11)Записать на языке предикатов: а) все аспиранты учатся;

б) некоторые спортсмены отличники.

7. Неклассические логики.

7.1 Введение.

Существует известный тезис Гильберта, что любое математическое утверждение может быть записано на языке логики предикатов, а любое математическое доказательство может быть проведено в рамках исчисления предикатов. Изученные в предыдущих разделах суждения (будь то простые или сложные) утверждали лишь факт их истинности или ложности. Такие суждения называются ассерторическими (лат. Assertorius – утвердительный). В рамках классической логики (логики высказываний и логики предикатов) многочисленные задачи решались в предложении именно таких высказываний. Однако этот формализм оказался неприменим для моделирования и решения большого многообразия задач, в которых достижение цели позволяет вводить предложения о допустимости, необходимости, возможности каких-то событий, явлений.

Теория неопределенности возникла в связи с решением практических вопросов принятия оптимальных решений в условиях неопределенности. В последнее время все больше ученых склоняется к тому, что неопределенность

– фундаментальный принцип, который следует принять за аксиому. В полностью детерминированных системах нет свободы выбора и, следовательно, нельзя получить оптимального решения. Имеется два основных типа неопределенностей:

1)вероятностная или стохастическая неопределенность;

2)лингвинистическая неопределенность.

Первая неопределенность обусловлена случайными факторами и подчиняется теории случайных процессов. Вторая связана с нечетким формированием целей или с расплывчатостью ограничений. Она формулируется в терминах теории нечетких множеств и изучается в нечеткой логике и в нечетких алгоритмах. Эти методы нашли широкое применение в теории управления для

расчета различных рисков.

Изучение этих ограничений подвело к разработке других логических систем, которые обычно называют неклассическими логиками. Существует

86

большое число неклассических логик. Мы ограничимся изучением только тех из них, которые используются в области искусственного интеллекта.

Неклассические логики можно объединить в две группы: одни конкурируют с классическими логиками, а другие являются их расширениями. К первой группе относятся пороговая логика интуиционистская логика и нечеткая логика. Во вторую группу входят модальные логики, которые подразделяются на временные, динамические и другие логики, многозначные логики.

7.2 Нечеткая и модальные логики.

Основоположник теории расплывчатых множеств и систем профессор компьютерных наук в университете Беркли (США) Лотус А.Заде впервые ввел понятие «пушистое», «нечеткое множество». Он использовал термин «функция принадлежности» и показал, что обычные количественные или точные методы анализа, хорошо разработанные для механических систем, не пригодны для исследования систем, степень сложности которых сравнима с гуманистическими, так как чем сложнее система, тем менее мы способны дать точные суждения о ее поведении. Основополагающим принципом нечеткой математики является так называемый принцип несовместимости: «высокая точность несовместима с большой сложностью системы».

Жертвуя точностью перед сложностью, вводят так называемые лингвистические переменные, т.е переменные, значениями которых являются не числа, а слова или предложения на естественном языке.

Подход с позиции теории нечетких множеств опирается на предпосылку о том, что элементами мышления человека являются не числа, а словесные описания, т.е элементы расплывчатых множеств или классов, для которых переход от « принадлежности» классу или «непринадлежности» не скачкообразен, а непрерывен. В дополнение к количественным характеристикам объектов использование словесных описаний позволяет анализировать достаточно сложные системы, недоступные формальному математическому анализу.

Основные определения теории нечетких множеств.

Нечетким множеством Ă на универсальном множестве U называется совокупность пар (µA (u), u), где µA (u) – степень принадлежности элемента u U к нечеткому множеству Ă.

Степень принадлежности – число из диапазона [0,1]. Чем выше степень принадлежности, тем в большей мере элемент универсального множества соответствует свойствам нечеткого множества.

Функцией принадлежности называется функция, которая позволяет вычислить степень принадлежности произвольного элемента универсального множества к нечеткому множеству.

87

Если универсальное множество состоит из конечного количества элементов U= { u1,u2,….,uk}, то нечетное множество Ă записывается в виде

Ă=∑ µ (ui)/ ui.

i=1…k

В случае непрерывного множества U используют обозначение

Ă=∫µ (u)/ u.

Лингвистической переменной называется переменная, значениями которой могут быть слова или словосочетания некоторого естественного или искусственного языка.

Терм-множеством называется множество всех возможных значений лингвистической переменной.

Термом называется любой элемент терм-множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности.

Дефазификацией называется процедура преобразования нечеткого множества в четкое число. В теории нечетких множеств процедура дефазификации аналогична нахождению характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры дефазификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности. Для многоэкстремальных функций принадлежности наиболее часто используется дефазификация путем нахождения центра тяжести плоской фигуры ограниченной осями координат и функцией принадлежности.

Основные понятия нечеткой логики

Будем обозначать фигурными скобками {} множества, а квадратные []и круглые () использовать для обозначения замкнутого и открытого интервала действительных чисел.

Пусть Х – произвольное непустое множество. Множество

= {}

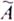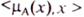Называется нечетким множеством в множестве Х, если каждый элемент

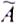множества есть пара, на первом месте которой стоит некоторое значение функции µ (х) ->[0,1], называемое функцией принадлежности элементов из Х множеству , а на втором – элемент для которого определена эта функция. Другими словами, при задании множеству 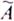каждому 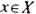приписывается число 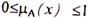,определяющее степень принадлежности этого элемента

88

множеству. Примем, что в множество не включаются элементы 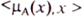, для которых .

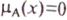Здесь и в дальнейшем, если это не вызывает недоразумений, знак ~ над нечетким множеством в записи функции принадлежности будем опускать.

Носителем нечеткого множества 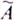называется подмножество Х, для которых значение функции принадлежности 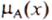больше нуля. Очевидно, что само множество Х можно формально рассматривать как расплывчатое в себе, если каждому приписать

Нечеткое множество в Х называется пустым 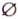, если для всех

величина 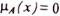. Ясно, что носитель пустого расплывчатого множества также пустое множество.

Примеры: Пусть		Множества
и	,	являются
нечеткими в множестве Х. Носителем множества	служит множество

, а носителем множества 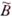является 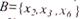.Отметим, что множество В фактически четкое в Х , так как значения функции принадлежности для всех элементов этого носителя равны единице. Исходя из этого, любое четкое подмножество множества Х может быть рассмотрено как нечеткое множество частного вида.

Нечетким высказыванием называется предложение, степень истинности или ложности которого принимает значения из интервала [0,1], причем 0 и 1 являются предельными значениями степени истинности и совпадают с понятиями лжи и истины для четких высказываний.

Нечеткое высказывание, имеющее значение степени истинности, равное 0.5 , назовем индифферентностью, так как оно истинно в той же мере, как ложно.

Поскольку в нечеткой логике степень истинности каждого высказывания рассматривается безотносительно к его смыслу, то нечеткое высказывание и его степень истинности будем обозначать одной и той же прописной буквой с тильдой.

Простые высказывания, связанные логическими операциями образуют, сложное высказывание.

Степень истинности отрицания нечеткого высказывания определяется

выражением

(7.1)

Отсюда ясно, что степень истинности 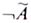зависит от степени

истинности .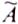

Степень истинности конъюнкции высказываний:

(7.2)

89

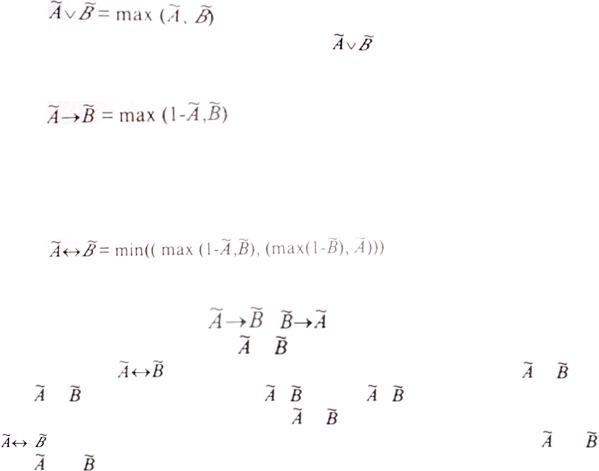
Степень истинности высказывания 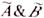совпадает со степенью истинности наименее истинного высказывания.

Степень истинности дизъюнкции высказываний:

(7.3)
Степень истинности высказывания	совпадает со степенью
истинности наиболее истинного высказывания.
Степень истинности импликации высказываний:

(7.4)

Из (7.4) следует, что степень истинности импликации не меньше степени истинности ее посылки или степени истинности ее следствия. Кроме того, степень истинности импликации тем выше, чем меньше степень истинности посылки или выше степень истинности следствия.

Степень истинности эквивалентности высказываний:

(7.5)

Отсюда следует, что степень истинности эквивалентности расплывчатых высказываний совпадает со степенью истинности менее

истинной из импликаций				и	. Если степени истинности
расплывчатых высказываний				и	одинаковы, то степень истинности
высказывания			лежит в интервале [0.5, 1] и имеет значение и			0.5
при	=	=0.5 и значение 1 при =			=1 или = = 0. При разных значениях
степеней истинности высказываний					и степень истинности высказывания
	может принимать значения от 0 до 1. причем значение 0 при					=0, =1
или	= 1	=0.
	Два высказывания называются расплывчато близкими, если степень

истинности высказывания больше или равна 0.5. В случае равенства 0.5 их называют расплывчато взаимно индифферентными.

Выражения (7.1) – (7.5) в случаях, когда степень истинности высказываний принимает только два значении 0 или 1 определяют соответствующие логические операции над четкими высказываниями.

Модальная, многозначная и пороговая логика.

Модальная логика – область логики, в которой наряду с обычными высказываниями рассматриваются модальные высказывания, т.е. высказывания, характеризующие степень достоверности суждений. Различают три типа модальностей:

-модальности общего вида: «необходимо», «возможно», «невозможно», «случайно»;

-модальности, связанные с характеристиками действий и поступками людей в обществе: «обязательно», «разрешено», «запрещено»;

-модальности, являющиеся характеристиками знаний: «доказано»,

«опровергнуто», «убежден», «сомневается».

90