Методичка

г) x y z д) xyz е) xyz xyz

ж) (x y)(x y)(x y)

Примечание: Для приведения к СДНФ, если в какой-либо конъюнкции не содержится переменной z, то из числа переменных, входящих в исходную формулу, надо добавить к этой конъюнкции член ( z z ) и применить закон распределительности конъюнкции относительно дизъюнкции (для приведения к СКНФ член zz соответственно).

xy(z z) xz(y y) xyz xyz xyz xyz .

12. Приведите следующие формулы к СДНФ с помощью равносильных преобразований:

а) (x y)(x y)	б) x y xy			в) xyz xy
г) x(y z)	д) (x y z)(x y z)			е) (x y)xy

13. Приведите следующие формулы к СКНФ с помощью равносильных преобразований и проверьте их с помощью таблиц истинности :

а) x xy	б) xy xy	в) xyz xyz
г) x(x y)	д) xyz xy

Примечание: (x yy) x 0 x x *1 (x yy) (x y)(x y) .

14. Найти все булевы функции от 2х переменных являющиеся:

а) линейными; б) монотонными; в) самодвойственными.

15.Установить является ли самодвойственной функция эквивалентности.

16.Привести пример монотонной функции, которая одновременно была бы линейной.

17.Убедиться, что функции Шеффера и Вебба не являются ни линейными, ни монотонными.

18.Минимизировать всеми известными вам способами функцию f(x1,x2,x3)|1=v(0,1,2,3,4,5).

19.Минимизировать с помощью карт Карно функцию f(x1,x2,x3,x4)|1=v(0,3,4,7,11,15).

20.Минимизировать с помощью метода Квайна Мак-Класки функцию f(x1,x2,x3,x4)|1=v(0,2,4,5,6,7,11,12,14,15).

21.Минимизировать с помощью карт Карно функцию в классе КНФ.

51

4.Введение в формальные (аксиоматические) системы.

4.1Формальные модели.

Современная процедура научного исследования состоит в том, что формальное изучение любой проблемы начинается с замены реальных объектов их абстрактными представлениями, выбираемыми таким образом, чтобы в этих моделях были отражены именно те свойства реальных объектов, которые мы должны изучать. Цель абстрагирования – выделение тех аспектов, которые существенны для решения проблемы и игнорирование тех аспектов, которые незначительны, усложняют проблему и делают анализ менее общим и эффективным.

При научном подходе, на уровне рационального исследования, мы имеем дело не с реальной действительностью, а со структурами, математическими абстракциями материальных процессов или объектов. Реальные процессы и объекты, как правило, бесконечно сложны. Абстракция применяется для того, чтобы ограничить эту сложность, дать возможность принимать правильные решения. С помощью абстрагирования человек строит формальные модели реальных процессов и явлений.

Такие формальные модели, будучи построенными, далее допускают анализ и преобразование с помощью формальных математических средств. Формальные модели позволяют выразить существенные для решения конкретной проблемы свойства процесса.

В точных терминах математического аппарата можно наглядно представить характеристики построенной модели, которые объясняют известные и предскажут новые свойства исследуемого реального процесса или объекта. Именно на основе такого научного подхода к решению инженерных проблем получено много впечатляющих результатов во многих областях техники. Это все подтверждает слова немецкого химика Бунзена: «Нет ничего более практичного, чем хорошая теория».

Вместо того, чтобы непосредственно начать преобразования реальных процессов или объектов ( т.е использовать чисто эмпирический подход к решению реальных задач, названный «метод проб и ошибок»), ученый вначале строит на основе абстракции математическую модель, а затем использует преобразование модели. Получая в результате преобразования и анализа модели какие-либо выводы, исследователь применяет их к той области реального мира, отображением которой является модель. Поскольку все абстракции неполны и неточны, можно говорить только о приближенном соответствии реальности тех результатов, которые получены исследованием на моделях. Соответствие связей и отношений объектов модели элементам реального мира называется адекватностью модели. Именно степень адекватности модели определяет, применимы ли результаты, полученные на модели, к конкретной проблеме реального мира. Часто адекватность модели обуславливается рядом условий и ограничений на сущности реального мира, и для того чтобы использовать результаты анализа, полученные на модели,

52

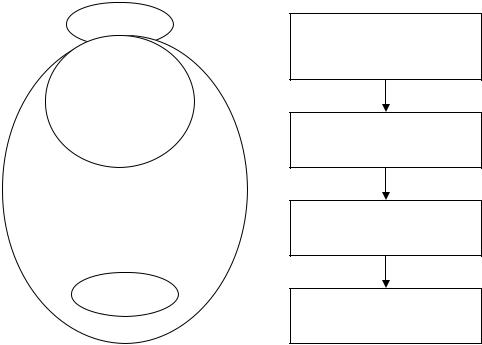
необходимо тщательно проверить эти условия и ограничения (или обеспечить их выполнение!). В противном случае по результатам оценки создается новая модель и повторяется итерационный цикл преобразования и нового анализа модели, что показано на рис 4.1 пунктирными линиями.

Преобразование, анализ

Модель

решение

на основе

модели

модели

(модели)

Абстрагирование

Мир идей

Интерпретация

модели

преобразование

Мир вещей

проблема

Результат

(реальность)

преобразования

Реальных объектов

(Исходные

объекты

реального мира)

Рис 4.1 Принцип математического моделирования.

Вместо того, чтобы начать преобразование реальных объектов вслепую в соответствии с рис 4.1 исследователь вначале строит математическую модель при помощи абстрагирования от конкретной проблемы и переходит в мир моделей, затем выполнением операций «преобразование модели» он получает оптимальное (или близкое к оптимальному) решение на модели и возвращается в мир реальных объектов, интерпретируя результаты моделирования. Если результат преобразования не устраивает исследователя, он усложняет модель и повторяет итерационный цикл, показанный на рис 4.1.

На рис 4.1 видны различия в задачах фундаментальных и прикладных наук. Фундаментальные науки занимаются разработкой абстрактных моделей, методов их преобразования и анализа. Они занимаются проблемами, лежащими в области мира идей.

Перед прикладной наукой стоит задача анализа реальных объектов, создания моделей реальных объектов путем абстрагирования от ненужных для анализа деталей реальности, важной является проблема выбора среди множества формальных моделей такой модели, в рамках которой исходная проблема имеет наиболее эффективное решение. После получения такого решения надо правильно интерпретировать результаты моделирования на реальную действительность.

53

4.2 Принципы построения формальных систем.

Формальные системы - это системы операций над объектами, понимаемыми как последовательность символов (т.е. как слова в фиксированных алфавитах), сами операции также являются операциями над символами. Термин "формальный" подчёркивает, что объекты и операции над ними рассматриваются чисто формально, без каких бы то ни было содержательных интерпретаций символов. Предполагается, что между символами не существует никаких связей и отношений, кроме тех, которые явно описаны средствами самой формальной системы.

Исторически теория формальных систем, так же как и теория алгоритмов, возникла в рамках оснований математики при исследовании строения аксиоматических теорий и методов доказательства в таких теориях. Всякая формальная теория определяется, во-первых, языком, т.е. некоторым множеством высказываний, имеющих смысл с точки зрения этой теории. Вовторых, совокупностью теорем - подмножеством языка, состоящим из высказываний, истинных в данной теории.

Вматематике с античных времён существовал образец систематического построения формальной теории - геометрия Евклида, в которой все исходные предпосылки сформулированы явно, в виде аксиом, а теоремы выводятся из этих аксиом с помощью цепочек логических рассуждений, называемых доказательствами. Однако, до середины 19 века математические теории, как правило, не считали нужным явно выделять все исходные принципы. Критерии же строгости доказательств и очевидности утверждений в разные времена были различными и явно не формулировались. Время от времени это приводило к необходимости пересмотра основ той или иной теории. Известно, например, что основания дифференциального и интегрального счисления, разработанные в 18 веке Ньютоном и Лейбницем в 19 веке, подверглись серьёзному пересмотру. Математический анализ в его современном виде опирается на работы Коши, Больцано и Вейерштрасса по теории пределов.

Вконце 19 века такой пересмотр затронул общие принципы доказательств в математических теориях. Это привело к созданию новой отрасли математики - оснований математики, предметом которой и стало построение аксиоматических теорий формальных систем, чтобы в них не возникало противоречий. Одной из фундаментальных идей, на которые опираются исследования по основаниям математики, является идея формализации теорий, т.е. последовательного проведения аксиоматического метода построения теорий.

При этом не допускается пользоваться какими-либо предположениями об объектах теории, кроме тех, которые выражены явно в виде аксиом; аксиомы рассматриваются как формальные последовательности символов (выражения),

аметоды доказательств— как методы получения одних выражений из других с помощью операций над символами. Такой подход гарантирует четкость исходных утверждений и однозначность выводов, однако может создаться впечатление, что осмысленность и истинность в формализованной теории не играют никакой роли. Внешне это так, однако, в действительности и аксиомы

54

и правила вывода стремятся выбирать таким образом, чтобы построенной с их помощью формальной теории можно было придать содержательный смысл.

Более конкретно формальная система (или исчисление) строится следующим образом.

1.Определяется некоторое счетное множество символов, т.е. множество, элементы которого могут быть взаимно однозначно сопоставлены элементам натурального ряда 1,2,...N, которые называется термами. Имеется другое конечное множество символов, элементы которого называются связками или операциями. Наконец, существует конечное множество вспомогательных символов. Конечные последовательности символов называются выражениями данной системы.

2.Определяется множество формул или правильно построенных выражений, образующее язык теории. Это множество задается конструктивными средствами (как правило, индуктивным определением) и, следовательно, перечислимо. Для правильно построенных формул (ППФ) задаются правила их конструирования, т.е. определяется эффективная процедура, с помощью которой по данному выражению выясняется, является ли формула правильно построенной в данной формальной системе (ФС) или нет. Формула, для которой существует такая процедура, называется разрешимой в данной ФС, в противном случае неразрешимой.

3.Выделяется подмножество формул, называемых аксиомами ФС. Так же как и для ППФ для аксиом должна иметься процедура, позволяющая определить, является ли ППФ аксиомой или нет. Подмножество может быть и бесконечным, во всяком случае, оно должно быть разрешимо.

4.Задается конечное множество R1, R2,..,Rk отношений между ППФ, называемых правилами вывода. Должна иметься эффективная процедура, позволяющая для произвольной конечной последовательности ППФ решить, может ли каждый член этой последовательности быть выведен с помощью

конечного числа правил вывода. Правило вывода R(F1, ..., Fn, G) —это вычислимое отношение на множестве формул. Если формулы F1, ..., Fn, G находятся в отношении R, то формула G называется непосредственно

выводимой из F1, ..., Fn по правилу R. Часто правило R(F1, ..., Fn, G) записывается в виде (F1, ..., Fn)/G. Формулы F1, ..., Fn называются посылками правила R, a G—его следствием или заключением. Примеры аксиом и правил вывода будут приведены несколько позднее.

Выводом формулы В из формул A1, ..., An называется последовательность формул F1, ..., Fm, такая, что Fm = B, а любая Fi(i = 1,...,m) есть либо аксиома, либо одна из исходных формул A1, ..., An, либо непосредственно выводима из формул F1, ..., Fi-1 (или какого-то их подмножества) по одному из правил вывода. Если существует вывод В из A1, ..., An, то говорят, что В выводима из A1, ..., An. Этот факт обозначается так: A1,...,An├ В. Формулы A1, ..., An называются гипотезами или посылками вывода. Переход в выводе от Fi-1 к Fi называется i-м шагом вывода.

Доказательством формулы В в теории Т называется вывод В из пустого множества формул, т. е. вывод, в котором в качестве исходных формул

55

используются только аксиомы. Формула В, для которой существует доказательство, называется формулой, доказуемой в теории Т, или теоремой теории Т; факт доказуемости В обозначается ├ В.

Очевидно, что присоединение формул к гипотезам не нарушает выводимости. Поэтому если ├В, то А├В, и если A1, ..., An ├ В, то A1, ..., An, An+1 ├ В для любых A и An+1. Порядок гипотез в списке несуществен.

Например, если удалось построить вывод В из A1, ..., An, то элементы последовательности ППФ A1, ..., An называются посылками вывода (или гипотезами). Сокращенно вывод В из A1, ..., An записывается в виде A1, ..., An ├ В, или если Г= A1,.., An то Г├ В. Напомним, что вывод ППФ без использования посылок есть доказательство ППФ В, а сама В – теорема, и это записывается ├ В.

Таким образом, любая формальная система задается четверкой: FS=<S,F,A,R>, где S — множество базовых элементов (символов -

алфавит); F — множество ППФ; А — система аксиом; R — множество правил вывода.

Множество S состоит из конечного или счетного множества элементов (термов, операций), из которых по правилам синтаксиса строятся синтаксически правильные совокупности (ППФ) формальной системы. Множеством аксиом может быть объявлено любое множество синтаксически правильных совокупностей. Применение семантических правил R (правил вывода) к элементам множества А позволяет строить семантически правильные совокупности (выводимые формулы). Соотношение между описанными множествами приведено на рис. 4 .2. На рис. 4 .3 изображена схема построения формальной аксиоматико-дедуктивной системы.

Алфавит

Множество

выводимых

формул

Множество правильно построенных формул

Аксиомы

Определяется формальный язык (алфавит) и набор синтаксических правил

Определяется множество аксиом

Определяются правила логического вывода

Определяются правильно построенные формулы

Рис 4.2 Схема формальной системы. Рис 4.3 Схема построения системы.

56

4.3. Аксиоматические системы. Формальный вывод.

Исторически понятие формальной теории было разработано в период интенсивных исследований в области оснований математики для формализации собственно логики и теории доказательств. Сейчас этот аппарат широко используется при создании специальных исчислений для решения конкретных прикладных задач.

Формальный вывод

Пусть F1, ..., Fn, G - формулы теории Т, то есть F1, ..., Fn, G являются ППФ. Если существует такое правило вывода R , что (F1, ..., Fn, G) R, то говорят, что формула G непосредственно выводима из формул F1, ..., Fn по правилу вывода R. Обычно этот факт записывают следующим образом:

	F1 ,..., Fn	R
	G		, где формулы F1, ..., Fn называются посылками, а формула G –
заключением.

ЗАМЕЧАНИЕ. Обозначение правила вывода справа от черты, разделяющей посылки и заключение, часто опускают, если оно ясно из контекста.

Если в теории Т существует вывод формулы G из формул F1, ..., Fn, то это записывают следующим образом:

F1, ..., Fn├ Т G, где формулы F1, ..., Fn называются гипотезами вывода, а G

–заключением. Если теория Т явно подразумевается, то ее изображение обычно опускают.

Если ├ Т G, то формула G называется теоремой теории Т, (то есть теорема

–это формула, выводимая только из аксиом, без гипотез).

Если Г├ Т G, то Г, ├ Т G, где Г и - любые множества формул (то есть при добавлении лишних гипотез выводимость сохраняется).

Правила вывода делятся на прямые и непрямые. Прямые правила вывода

– это правила непосредственного перехода от одних формул к другим, т.е. переход от посылки к заключению. Им сопоставляются определенные шаги формального вывода. Существует несколько стандартных прямых правил вывода, включающих следующие:

1.Прямое рассуждение. Предполагаем, что высказывание А истинно и показываем справедливость В. Такой способ доказательства исключает ситуацию, когда А истинно, а В ложно, поскольку

именно в этом случае импликация (А В) принимает ложное значение. В качестве примера докажем прямым способом, что произведение xy двух нечетных чисел всегда нечетно. Действительно, любое нечетное число можно представить в виде х=2m+1, y=2n+1; тогда xy= (2m+1)(2n+1)= 4mn+2m+2n+1=2(2mn+m+n)+1, что тоже является нечетным числом.

57

2.Обратное рассуждение. Предполагаем, что высказывание В ложно и показываем ошибочность А. То есть, фактически, прямым способом проверяем истинность импликации применив закон контрапозиции. Именно так раньше было доказано, что если n2 нечетно, то и n нечетно. По закону контрапозиции нужно показать прямым способом рассуждений, что четность n влечет четность его квадрата. Действительно, если n=2m, то n2=4m2=2(2m2).

3.Метод «от противного». Предположив, что высказывание А истинно, а В ложно, используя аргументированное рассуждение, получаем противоречие. Этот метод основан на том, что импликация ложна в том и только в том случае, когда А истинно, а

В ложно.

Непрямые правила вывода - суть правила перехода от одних формальным выводов к другим. Таким правилам соответствуют мета утверждения о преобразованиях одних формальных выводов в другие. Непрямым правилом вывода является метод резолюции, введенный Дж. Робинсоном, который будет изложен позже.

Еще одним интересным способом рассуждения, который может быть оформлен в виде непрямого производного правила, является метод доказательства от противного. Суть его сводится к следующему. Пусть нам надо доказать вывод формулы А из посылок Г. Тогда применяют следующий формальный прием: отрицание формулы А добавляют к множеству формул Г и пытаются получить из посылок А, Г противоречие. Если такое противоречие получено, то это означает, что можно построить вывод А из Г

Синтаксис формальных систем.

Синтаксисом называется набор правил конструирования ППФ.

Семантика формальных систем.

Семантикой называется набор правил интерпретации формул.

Интерпретация в формальных системах.

Интерпретацией называется приписывание формуле одного из двух значений истинности: 1 (истинно) или 0 (ложно). Композиционность семантики заключается в том, что значение истинности некоторой формулы зависит от значений истинности составляющих высказываний и структуры формулы.

Общезначимость и непротиворечивость формул.

Формула называется общезначимой (или тавтологией), если она истинна в любой интерпретации. Формула называется противоречивой, если она ложна в любой интерпретации. Выполнимой называется формула, для которой существует хотя бы одна интерпретация, для которой она истинна. Опровержимой называется формула, для которой существует хотя бы одна интерпретация, для которой она ложна.

Формула, которая есть пропозициональная переменная или отрицание переменной, называется литералом.

Произвольная конъюнкция литералов называется конъюнктом или элементарной конъюнкцией, произвольная дизъюнкция литералов называется

58

дизъюнктом или элементарной дизъюнкцией. Для того, чтобы элементарная конъюнкция была тождественно ложной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание. Для того, чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы в ней содержалась переменная и ее отрицание.

Фундаментальная проблема логики, называемая проблемой дедукции, состоит в том, чтобы определить, является ли формула G логическим следствием множества формул Г. Само слово дедукция (лат. deductio – выведение) определяется как логическое умозаключение от общих суждений к частным или другим общим суждениям. Если логическим следствием из множества формул Г является формула А, имеющая значение истинности Л (ложь или 0), то говорят, что формула А невыполнима. Именно в этом и состоит принцип дедукции: формула А является логическим следствием множества формул Г тогда и только тогда, когда Г А невыполнима.

4.4Проблемы аксиоматического исчисления формальных систем.

Всякая аксиоматическая теория для ее обоснования требует рассмотрения четырех проблем:

проблемы полноты;

проблемы независимости;

проблемы разрешимости;

проблемы непротиворечивости.

Полнота. Формальная теория называется полной (или адекватной) в широком смысле, если любая тождественно истинная формула в ней доказуема. Формальная теория называется полной в узком смысле, если добавление к списку ее аксиом любой недоказуемой формулы в качестве новой аксиомы приводит к противоречивому исчислению.

Если для множества (алгебраической системы) M существует формальная полная непротиворечивая теория, то M называется аксиоматизируемым (или формализуемым) множеством.

Независимость. Система аксиом (или аксиоматизация) называется независимой, если никакая из аксиом не выводима из остальных.

Разрешимость. Еще одна важная характеристика формальной теории – это ее разрешимость. Формальная теория называется разрешимой, если существует алгоритм, который для любой формулы данной теории определяет, является она теоремой (т.е. доказуемой) или нет. Формула, для которой такая процедура существует, называется разрешимой в этой теории, в противном случае – неразрешимой.

Простейшим примером проблемы разрешимости является проблема разрешимости алгебры логики, в которой она состоит в отыскании алгоритма, позволяющего для каждой формулы алгебры логики установить, является ли она тождественно истинной или тождественно ложной или выполнимой.

59

Например, исчисление высказываний разрешимо, а исчисление предикатов неразрешимо. Разрешающий алгоритм для любой формулы F исчисления высказываний заключается в вычислении значений F на всех наборах значений ее переменных.

Исчисление предикатов неразрешимо. Несмотря на полноту исчисления предикатов, разрешающий алгоритм, связанный с вычислением значений истинности предикатных формул, построить не удается из-за бесконечности предметной области, которая приводит в общем случае к бесконечным таблицам истинности.

Непротиворечивость. Напомним, что формула называется противоречивой, если она ложна в любой интерпретации. Такое определение противоречивой формулы является семантическим, т.е. связывающим непротиворечивость с истинностью. Исходя из него, можно сформулировать понятие семантически непротиворечивой теории.

Формальная теория Т называется семантически непротиворечивой, если ни одна ее теорема не является противоречием. Таким образом,

формальная теория пригодна для описания тех множеств (алгебраических систем), которые являются ее моделями. Модель для формальной теории Т существует тогда и только тогда, когда Т семантически непротиворечива.

Формальная теория Т называется формально непротиворечивой, если в ней не являются выводимыми одновременно формулы F и F.

Теория Т формально непротиворечива тогда и только тогда, когда она семантически непротиворечива.

4.5Метатеория формальных систем.

При изучении формальных теорий мы имеем дело с двумя типами высказываний. Во-первых, с высказываниями самой теории (теоремами), которые рассматриваются как чисто формальные объекты, определенные ранее, а во-вторых, с высказываниями о теории (о свойствах ее теорем, доказательств и т.д.), которые формулируются на языке, внешнем по отношению к теории, - метаязыке и называются метатеоремами. Различие между теоремами и метатеоремами не всегда будет проводиться явно, но его обязательно надо иметь в виду.

Под метатеорией формальных систем понимается изучение их общих свойств и соответствия этих свойств целям, ради которых они создавались. Ценность всякой формальной теории, в конечном счете, определяется ее способностью описывать какие-то объекты реального мира и связи между ними. Поэтому один из первых для любой теории вопросов – это вопрос о том, для описания каких объектов пригодна данная теория. Конечно, если ставить его как общую проблему соответствия научных знаний о мире самому миру, то он не может обсуждаться средствами одной математики без привлечения философии и методологии науки. Более узко проблема адекватности формальной теории и описываемых ею объектов может рассматриваться как

60