Методичка

математическая задача о соответствии между содержательно построенной теорией, рассматриваемой как множество объектов с операциями и отношениями на нем и множеством высказываний об этой теории, построенном как формальное исчисление. При такой постановке задачи интуитивно ясное понятие интерпретации приобретает точный математический смысл.

Интерпретацией формальной теории Т в область интерпретации M называется функция I : F M, которая каждой формуле формальной теории однозначно сопоставляет некоторое содержательное высказывание относительно объектов множества (алгебраической системы) M. Это высказывание может быть истинным или ложным. Если соответствующее высказывание является истинным, то говорят, что формула выполняется в М.

Интерпретация I называется моделью множества формул , если все формулы этого множества выполняются в интерпретации I. Интерпретация I называется моделью формальной теории Т, если все теоремы этой теории выполняются в интерпретации I, (то есть все выводимые формулы оказываются истинными в данной интерпретации).

Чисто логические теории – исчисление высказываний и исчисление предикатов пригодны для описания любых множеств, что соответствует общенаучному принципу универсальности законов логики. Лейбниц формулировал его как выполнимость логических законов во всех «мыслимых мирах». Аналогом этого критерия, сформулированным в терминах самих формальных теорий без привлечения семантических понятий, является формальная или дедуктивная непротиворечивость.

Главная цель формальной теории состоит в том, чтобы разработать такие правила оперирования формальными структурами, которые могли обеспечить последовательность, правильность и доказуемость выводов или другими словами истинность рассуждений.

4.6Вопросы для самопроверки.

1.Как строятся аксиоматические системы?

2.Назовите основные понятия теории формальных систем.

3.В чем заключается непротиворечивость и полнота формальных систем?

4.Назовите основные составляющие части формальных систем?

5.В чем заключается принцип логического вывода?

6.В чем заключается разрешимость формальных систем?

7.Дать основные понятия аксиоматических систем.

8.В чем заключается метод использования формальных моделей при исследовании систем?

9.Разрешимо ли исчисление высказываний и исчисление предикатов?

10.Что такое синтаксис и семантика формальных систем?

61

5. Исчисление высказываний.

5.1 Исчисление высказываний. Основные понятия и определения.

Простейшим разделом математической логики является исчисление высказываний. Элементарные высказывания рассматриваются в ней как нерасчленяемые "атомы", а составные высказывания - как молекулы, образованные из "атомов" применением логических операций.

Пусть X, Y и Z - переменные, вместо которых можно подставлять любые элементарные высказывания (или их значения истинности). Такие переменные могут быть названы высказывательными (или булевыми). С помощью высказывательных переменных и символов логических операций любое высказывание можно формализовать, т.е. заменить формулой, выражающей его логическую структуру. Например, "Если число делится на 2 и на 5, то оно делится на 10 (X У) 10”.

Кроме сложных логических высказываний в исчислении высказываний широко используются еще и секвенции. Если формулы исчисления высказываний можно рассматривать как формы сложных высказываний, то секвенции являются формализацией утверждений и теорем, в которых можно отчетливо выделить условия (посылки) и заключения. Секвенциями называются выражения следующего типа:

1. А1, А2,…,Аn ├ В, где n>0, A1, ..., An, В любые формулы. Читается «из А1, А2,…,Аn следует В».

Например, если удалось построить вывод В из A1, ..., An, то элементы последовательности ППФ A1, ..., An называются посылками вывода (или гипотезами). Сокращенно вывод В из A1, ..., An записывается в виде A1, ..., An ├ В, или если Г= A1,.., An то Г├ В. Напомним, что вывод ППФ без использования посылок есть доказательство ППФ В, а сама В – теорема, и это записывается ├ В.

2.├ В, читается «В доказуемо».

3.А1, А2,…,Аn ├ читается «система А1, А2,…,Аn противоречива.

Так как исчисление высказываний является формальной аксиоматической системой, то в ней основным понятием является понятие пропозициональной формулы (ПФ).

Понятие ПФ вводится индуктивно:

1.Символы логических констант 0, 1 являются ПФ.

2.Каждая логическая переменная является ПФ.

3.Если А и В суть ПФ то A , А В, А В, А В, А В также ПФ.

4.Никаких других ПФ в логике высказываний нет.

Определение закончено. В нем 1 и 2 являются базисными пунктами, где указываются объекты множества, 3 - индуктивный пункт, где даны правила получения из базисных объектов новых объектов, которые будут именоваться

62

этим же термином, 4 - косвенный пункт, где указано, что заданный список исчерпывается.

Таким образом, синтаксис позволяет выделить формулы из произвольных соединений символов. Для графической модели первое и второе правило, называемое базисом, сопоставляет высказывания висячим узлам графического дерева, а третье, называемое индукционным шагом, порождает дерево, корнем которого является связка, называемая главной связкой формулы. Четвертый пункт является заключительным и указывает на корень графического дерева. Например, для формулы (А В)&(C D) имеем дерево

рис.5.1 Диаграмма формализации.

Процедура формализации высказывания состоит из этапов:

1.Если высказывание простое, то ему ставится в соответствие элементарная формула.

2.Если высказывание составное, то нужно:

а) выделить все элементарные высказывания и логические связки, образующие составное высказывание;

б) заменить их соответствующими символами; в) расставить скобки в соответствии с символами.

Элементами логических рассуждений являются утверждения, которые либо истинны, либо ложны, но не то и другое вместе. Такие утверждения называются (простыми) высказываниями. Простые высказывания считаются пропозициональными переменными, принимающими истинностные значения «И» и «Л». Из простых высказываний с помощью логических связок могут быть построены составные высказывания. Обычно рассматривают следующие логические связки:

Название	Прочтение	Обозначение
Отрицание	не
Конъюнкция	и	&
Дизъюнкция	или
Импликация	если ... то

Формулы.

Правильно построенные составные высказывания называются (пропозициональными) формулами. Формулы имеют следующий синтаксис:

63

<формула>::=И | Л | <пропозициональная переменная>| ( <формула>) | (<формула> & <формула>) | (<формула> <формула>) | (<формула> <формула>)

Для упрощения записи вводится старшинство связок ( ,&, , ) и лишние скобки опускаются.

Формула, которая есть пропозициональная переменная или отрицание переменной называется литералом. Произвольная конъюнкция литералов называется конъюнктом или элементарной конъюнкцией, произвольная дизъюнкция литералов называется дизъюнктом или элементарной дизъюнкцией.

Исчисление высказываний как формальную теорию можно определить с помощью аксиоматического метода.

Классическое определение исчисления высказываний:

1. Алфавит: ¬ и → - связки (логический базис Фреге)

(,) - служебные символы.

a, b, ..., a1, b1,... - пропозициональные переменные.

2. Формулы: 1)переменные суть формулы.

2)если А,В - формулы, то (¬А) и (А→В) - формулы.

3) Никаких других формул в исчислении высказываний

нет.

3. Аксиомы. Приведем здесь две системы аксиом. Первая из них состоит из 11 формул, поделенных на 4 группы, и непосредственно использует все логические связки:

Система аксиом I

I.1. А→(В→А); из ложной посылки следует все, что угодно.

2.(A→ (B → С))→((А→В)→(A→С));

II. 3. (А&В)→А; конъюнкция сильнее любого из его членов;

4.(А&В)→В;

5.А→(В→(А & В));

III. 6.A→(A B); дизъюнкция слабее каждого из своих членов;

7.B→(A B);

8.(A→С)→((B→С)→((A B)→ C));

IV. 9. (А→В)→( ¬B →¬A); закон контрапозиции;

10.A→¬¬A; двойное отрицание равносильно утверждению;

11.¬¬A→A.

Другая система использует только две связки ¬ и →; при этом сокращается алфавит исчисления (выбрасываются знаки , &) и соответственно изменяется определение формулы. Операции , & рассматриваются не как связки исчисления высказываний, а как сокращения (употреблять которые удобно, но не обязательно) для

64

некоторых его формул: А В заменяет ¬A→B, А&В заменяет ¬(А→¬В). Таким образом :

1)А В=¬A→B;

2)А&В= ¬(А→¬В);

3)А В = (А В) (В А) .

Врезультате система аксиом становится намного компактнее.

Система аксиом II

II.1. A→(B→A);

II.2. (А→(В→С))→((А→В)→(А→С)); II.3 (¬В→¬А)→((¬В→А)→В ).

Приведенные системы аксиом равносильны в том смысле, что

порождают одно и то же множество формул. Разумеется, такое утверждение нуждается в доказательстве, которое заключается в том, что показывается выводимость всех аксиом системы II из аксиом системы I и, наоборот, системы I из системы II (с учетом замечаний относительно и &). Доказательство этих выводов предоставляется читателю после того, как он познакомится с примерами вывода в исчислении высказываний.

Возможны и другие системы аксиом, равносильные первым двум системам.

Какая из систем лучше? Это зависит от точки зрения. Система II компактнее и обозримее; соответственно более компактны и доказательства различных ее свойств. С другой стороны, в более богатой системе I короче выводы различных формул.

4.Правила вывода:

1.Если А - тавтология, то заменяя в ней букву Х всюду, где она входит, произвольной формулой В, получаем также тавтологию (правило подстановки).

2.Если А и А→В суть тавтологии, то В - также тавтология

(правило заключения).

Первое из этих правил очевидно, а второе непосредственно следует из закона modus ponens.

Формула называется выводимой в исчислении высказываний, если она может быть получена из конечной совокупности исходных формул путём конечного числа шагов применения правил вывода.

Вообще говоря, не все тождественно - истинные формулы могут быть выведены из произвольного множества тавтологий. В то же время строго доказано, что можно выбрать такую конечную совокупность исходных тавтологий (аксиом вычисления высказываний), из которых выводимы все тождественно истинные формулы. Это важное положение решает проблему полноты исчисления высказываний. Другими словами свойство аксиоматической теории, заключающееся в том, что если формула А выражает логический закон (как например, тождественно-

65

истинная формула), то она выводима в этой теории, называется полной аксиоматической теорией.

Исчисления высказываний есть полная аксиоматическая теория.

Интерпретация

Пусть A(x1, ..., xn) - пропозициональная формула, где x1, ..., xn - входящие в нее пропозициональные переменные. Конкретный набор истинности значений, приписанных переменным x1, ..., xn, называется интерпретацией формулы А. Формула может быть истинной (иметь значение И=1) при одной интерпретации и ложной (иметь значение Л=0) при другой интерпретации. Значение формулы А в интерпретации I будем обозначать I(A). Формула, истинная при некоторой интерпретации, называется выполнимой. Формула, истинная при всех возможных интерпретациях, называется общезначимой (или тавтологией). Формула, ложная при всех возможных интерпретациях, называется невыполнимой (или противоречием).

Пример.

A A – тавтология. A& A – противоречие, A A – выполнимая формула, она истинна при I(A)=0.

5.2 Логическое следование. Принцип дедукции.

Говорят, что формула В логически следует из формулы А, если формула В имеет значение 1 при всех интерпретациях, при которых формула А имеет значение 1. Говорят, что формулы А и В логически эквивалентны (обозначается А↔B или просто А=В), если они являются логическим следствием друг друга. Логически эквивалентные формулы имеют одинаковые значения истинности при любой интерпретации.

Наиболее краткий и простой способ вывода основан на теореме дедукции.

Теорема дедукции определяет условия, при которых можно проверить правильность схемы рассуждений без использования таблиц истинности. Именно на этой теореме основаны все методы логического вывода, как в логике высказываний, так и в логике предикатов. Поэтому ее можно назвать основной теоремой теории логического вывода.

Теорема 5.1 Формула R является логическим следствием формул

тогда и только тогда, когда формула общезначима.

Доказательство. (Необходимость). Предположим, что R является логическим следствием формулы и докажем при этом предположении, что общезначима. Пусть I есть произвольная интерпретация атомарных высказываний. Если все истинны на I, то истинна на I и по определению логического следствия R истинна на I, и, следовательно, на этой интерпретации истинна. Если же

66

хотя бы одна ложна на I, то на этой интерпретации ложна, но 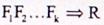также истинна независимо от R в силу определения импликации.

Следовательно, на любой интерпретации I формула истинна. В силу произвольности интерпретации I этот вывод справедлив для всякой

интерпретации, поэтому формула общезначима. (Достаточность). Предположим, что формула общезначима.

Тогда для всякой интерпретации, на которой все истинны, формула

тоже истинна, и поскольку общезначима, на этой интерпретации R тоже истинна в силу определения импликации.

Теорема 5.2 Формула R является логическим следствием формул

тогда и только тогда, когда формула невыполнима.

Доказательство. По теореме 5.1 формула R является логическим следствием формул тогда и только тогда, когда формула общезначима или, что то же, отрицание формулы невыполнимо. Но по закону де-Моргана

равносильно . Теорема доказана.

На основании теорем 5.1 и 5.1 вопрос о правильности схемы рассуждения сводится к проверке общезначимости либо невыполнимости некоторой формулы. Эта проверка может быть выполнена множеством различных способов.

Как, анализируя формулу в нормальной форме, можно сделать вывод о ее общезначимости или невыполнимости? Возьмем ДНФ, то есть представление

формулы в виде дизъюнкции конъюнкций . Для того чтобы сделать вывод о ее общезначимости, нужно анализировать всю формулу целиком: каждая конъюнкция общезначимой формулы может быть истинной только на нескольких интерпретациях. В то же время вывод о невыполнимости дизъюнкции конъюнкций можно сделать легко: каждая конъюнкция ДНФ невыполнимой функции должна быть невыполнима, а это очень легко проверить: конъюнкция литер невыполнима тогда и только тогда, когда она содержит хотя бы одну пару противоположных литер. Очевидными следствиями предыдущих теорем являются:

Теорема 5.3 Для того, чтобы формула R была логическим следствием

формулы , необходимо и достаточно , чтобы каждый конъюнкт дизъюнктивной нормальной формы представления формулы

содержал пару противоположных литер .

Теорема 5.4. Для того , чтобы формула R была логическим следствием формул ., необходимо и достаточно, чтобы

67

каждый дизъюнкт конъюнктивной нормальной формы представления содержал пару противоположных литер.

5.3Основные схемы логически правильных рассуждений.

Наряду с алфавитом и правилами построения сложных высказываний - логических формул, язык логики высказываний содержит правила преобразования логических формул. В алгебре логики - это эквивалентные соотношения, а также правило подстановки и правило замены; в исчислении высказываний - это общие логические аксиомы и правила подстановки и заключения, называемые правилами вывода. Правила преобразования реализуют общие логические законы и обеспечивают логически правильные рассуждения. Корректность допустимых в логике преобразований является фундаментальным свойством формальной (математической) логики.

Процесс получения новых знаний, выраженных высказываниями, из других знаний, также выраженных высказываниями, называется рассуждением (умозаключением). Исходные высказывания называются посылками (гипотезами, условиями), а получаемые высказывания – заключением (следствием). Приведенные ниже правила следует трактовать следующим образом: из истинности левой части следует истинность правой части. В формулах использован знак следования ├. Кроме того А и В – формулы, а Г –

некое множество формул (гипотез), возможно пустое.

В1. Введение конъюнкции: А,В├А&В

В2. Удаление конъюнкции: А&В ├А, А&В ├В;

В3. Отрицание конъюнкции: ¬ (А&В) ├¬А ¬В;

В4. Введение дизъюнкции: А├А В, В├А В;

В5. Элиминация (удаление) дизъюнкции А В, ¬В├А; А В, ¬А├В;

В6. Отрицание дизъюнкции (закон де Моргана):

¬(А В) ├¬А&¬В;

В7. Элиминация (удаление) импликации (modus ponens): А→В, А├В;

В8. Элиминация (удаление) импликации (modus tollens):

А→В, ¬В├ ¬А;

В9. Отрицание импликации: ¬(А→В)├А& ¬В;

В10. Введение эквиваленции:

А→В, В →А├ А В;

В11. Элиминация эквивалентности:

А В ├ А →В;

В12. Введение двойного отрицания:

А├ ¬ ¬А;

В13. Элиминация двойного отрицания:

¬¬А ├ А;

В14. Правило дедукции:

68

(Г,А ├В) ├(Г ├ А→В);

В 15. Доказательство от противного:

(Г, ¬А ├В & ¬В) ├(Г ├А);

В 16. Сведение к абсурду:

(Г,А ├В & ¬В) ├(Г ├ ¬А).

Приведем примеры наиболее употребляемых схем логически правильных рассуждений, записанных в несколько иной форме:

1. Правило заключения - утверждающий модус (Modus Ponens): "Если из высказывания А следует высказывание В и справедливо

(истинно) высказывание А, то справедливо В" ( Способ спуска). Обозначается:

АВ, А

В.

2.Правило отрицания - отрицательный модус (Modus Tollens):

"Если из А следует В, но высказывание В неверно, то неверно А”

(Доказательство от противного). Обозначается:

А В, ВА .

3. Правила утверждения-отрицания (Modus Ponendo-Tollens): "Если справедливо или высказывание А, или высказывание В (в

разделительном смысле) и истинно одно из них, то другое ложно" (разделительный силлогизм). Обозначается:

А В, А		А В, В
В ;		А .

4. Правила отрицания-утверждения (Modus Tollen-Ponens):

а) "Если истинно или А или В (в разделительном смысле) и неверно одно из них, то истинно другое":

	А В, А			А В, В
	В		;	А		.
б) "Если истинно А или В (в неразделительном смысле) и неверно одно
из них, то истинно другое" (Дизъюнктивный силлогизм). Обозначается:
	А В, А			А В, В
	В		;	А .

5. Правило транзитивности (упрощенное правило силлогизма): "Если из А следует В, а из В следует С, то из А следует С"

(гипотетический силлогизм). Обозначается:

А В, В С

А С .

6. Закон противоречия:

"Если из А следует В и ¬В, то неверно А":

А В, А ВА .

7. Правило контрапозиции:

"Если из А следует В, то из того, что неверно В, следует, что неверно А":

69

А ВВ А .

8. Правило сложной контрапозиции:

"Если из А и В следует С, то из А и ¬С следует ¬В":

( А & B) C

( A & C) B .

9. Правило сечения:

"Если из А следует В, а из В и С следует D, то из А и С следует D":

A B, (B & C) D

( A & C) D	.

Приведем без пояснений еще несколько правил умозаключений. 10. Правило импортации (объединения посылок):

A (B C)

( A & B) C .

11. Правило экспортации (разъединения посылок):

( A & B) C

A (B C) .

12. Правила дилемм:

A C, B C, A B

а)		C	(простая конструктивная дилемма);
		A B, C D, A C
б)		B D	(сложная конструктивная дилемма);
		A B, A C, B C
в)		A		(простая деструктивная дилемма);
		A B, C D, B D
г)		A C		(сложная деструктивная дилемма).

Примечание. Для построения логических формул, отражающих указанные выше логически правильные рассуждения, следует все посылки соединить связкой "И" (&) и полученную таким образом обобщенную посылку - связкой "если ..., то ..." (→).Например, правило заключения (Modus Ponens) должно быть представлено логической формулой:

A B, A ((A B) & A) B B

Примерами рассуждений, не являющихся правильными, могут служить:

	A B, B
а)	A
	A B, A
б)	B
	A B, A
в)	B и др.

Для того чтобы проверить, является ли данное умозаключение логически правильным, следует восстановить схему рассуждения и определить, относится ли она к схемам логически правильных рассуждений. Однако такая проверка осложняется тем, что схем логически правильных рассуждений

70