21. Понятие множества. Способы задания множеств. Чёткие и нечёткие, конечные и бесконечные множества

Имеется два существенно различных способа задания множеств. Можно либо перечислить все элементы множества, либо указать правило для определения того, принадлежит или не принадлежит рассматриваемому множеству любой данный объект. Таким образом, множество можно задать с помощью перечисления или с помощью описания.

При перечислении множества его элементы принято заключать в фигурные скобки:  — множество четных чисел, — множество чисел кратных трем. Под многоточием в данных случаях подразумеваются все последующие числа: в первом случае — четные, а во втором — кратные трем.

С другой стороны, для задания (описания) некоторого множества , состоящего из элементов, обладающих свойством, используют запись. Читается как: «— множество элементовтаких, что". Например,и — множество натуральных чисел, меньших 7.

Примеры в лингвистики – модификаторы «слегка» «или» «очень» «самый» и т.д.

22. Отношения между множествами. Основные операции над множествами.

Операции над множествами

1. Сравнение множеств

Множество А называется подмножеством множества В, если все элементы множества А содержатся во множестве В.

Два множества называются равными, если они содержат одинаковые наборы элементов.

ТЕОРЕМА

• Пустое множество Ø является подмножеством всех множеств.

• Универсальное множество U содержит все множества.

• Если , то В надмножество А.

ПРИМЕР

    А={0, 1, 2, 3},    В={0, 1}, .

          

2. Объединением двух множеств называется множество, содержащее все элементы обоих множеств.

ПРИМЕР

    А={К, А, Т, Я},   В={К, О, С, Т, Я}, 

 .

        

3. Пересечением  двух множеств называется множество, состоящее из общих элементов обоих множеств.

ПРИМЕР

А={К, А, Т, Я},   В={К, О, С, Т, Я},    ={К, Т, Я}.

 

4. Разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В.

ПРИМЕР

      А={К, А, Т, Я},    В={К, О, С, Т, Я},    А \ В={A},    В \ А ={О, С}.

5. Симметрической разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В и всех элементов множества В не содержащихся в А.

                        

ПРИМЕР

      А={К, А, Т, Я},    В={К, О, С, Т, Я},    А Δ В={A,О,С}.

  

6. Дополнением  (дополнением  до универсального множества) множества А называется множество, состоящее из всех элементов универсального множества не содержащихся в А.

7. Прямым или декартовым произведением множеств A и B, называется множество всех упорядоченных пар (a, b), где первый элемент a из множества A, а второй элемент b из множества B.

ПРИМЕР

, 

Степенью множества называется декартовое произведение множества A само на себя n раз.

ПРИМЕР

, .

Свойства операций над множествами

1)          Коммутативность.

2)          Ассоциативность.

3)          Дистрибутивность.

4)          Закон поглощения.

5)          Идемпотентность.

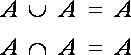
6)          Инволютивность.

7)          Свойство нуля.

АØ=А

АØ= Ø

8)          Свойство единицы.

9)           Закон де Моргана

Отношения между множествами

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие множествам А и В одновременно, то говорят, что эти множества пересекаются. Например, пусть множество А={a,b,c,d,e} и B = {b, c, d, k, l}. Элементы b, d принадлежат и множеству А, и множеству В. Значит, множества А и В имеют общие элементы, а сами множества пересекаются: АВ. 

Если множества не имеют общих элементов, например, А = {1, 2, 3} и B = {4, 5},то они не пересекаются: А В.

Иногда приходится рассматривать не все множество, а только его часть. Например, не все множество натуральных чисел, а только множество простых чисел. Тогда речь идет о подмножестве. Если любой элемент множества А  принадлежит так же и множеству В, то А называют подмножеством  В. Записывают АВ. Знак называютзнаком включения.

Любое множество является подмножеством самого себя, т.е. АА. Пустое множество является подмножеством любого множества: ¾А.  Все множества являются подмножествами одного и того же множества, называемого универсальным U.

Количество подмножеств множества, состоящего из n элементов равно . В нашем примере множество состоит из трех элементов, значит количество подмножеств равно=8.

Если множества состоят из одинаковых элементов и их количество равно, и каждый элемент множества  А  является элементом множества  В и наоборот, то  АВ и ВА  и говорят, что множества А и В равны: А=В. Например, А={a, d, c, d},  B={c, b, d, а}, значит  А=В. Для равных множеств порядок их элементов не является существенным.

Таким образом, между множествами возникают следующие отношения: множества могут пересекаться, не пересекаться, быть равными и включаться одно в другое.

Для наглядности употребляют изображения множеств на плоскости, которые называют диаграммами Эйлера-Венна(множества наглядно представляют в виде кругов, овалов), где штриховкой обозначают нужные области. Тогда вышеперечисленные отношения можно изобразить следующим образом.

Нередко бывает так, что рассматривают только подмножества одного и того же множества I. Такое множество I называют универсальным множеством. Так, если А – множество студентов первого курса, В – множество студенток в этом же институте, С – множество спортсменов этого же института, то в качестве универсального множества I можно взять множество студентов данного института, потому, что тогда АI, BI, CI.На диаграммах Эйлера-Венна универсальное множество часто изображается в виде прямоугольника, а его подмножества – кругами.

Различные числовые множества можно изображать на числовой прямой. Пусть а и b различные числа такие, что а<b. Тогда их запись и изображение таково: