УП_Вычисл_матем_Кузина-Кошев

Тогда

b	N xi	N	1			N	m
F(a,b) f (x)dx f (x)dx h
			f		(s)ds h Pk f (sk )
a	i 1 x	i 1	0			i 1	k 0
	i 1
N	m	N	m
h Pk f (xi 1 hsk ) h Pk f (xi 1 hsk ).
i 1	k 0	i 1 k 0

Тогда для трехточечного шаблона формула Чебышева имеет вид:

	h	N				1		1
		f xi h				2		4
	3 i 1

IN f b			f (x)dx
		a										(64)
				h		1			1
2										2
		f xi			f xi h		2		4		.
				2

8.2.6. Квадратурная формула Гаусса

Для получения квадратурной формулы отыскиваются оптимальные значения узлов интегрирования si и коэффициентов ci квадратурной

m

формулы I f ci f (si ) одновременно.

i 0

Потребуем точности формулы для полиномов степени, меньшей либо равной ( 2m 1).

Учитывая, что I (sm ) 1 sm dx												sm 1						1					1			, получим систему (
												m 1									m 1
						0												0
алгебраических уравнений с ( 2m 2 ) неизвестными:
c	0	c ..... c								m	1;
					1														1
c		s		c s			..... c						m	s	m						;
	0		0			1 1													2
				2			2									2						1
																								;
c0 s0					c1s1			..... cm sm														3
............................................
				2m 1					2m 1															2m 1				1
c	0	s	0			c s					..... c									m	s		m						.
							1	1																				2(m 1)

Например, при m = 2 получим следующую формулу:

		1														5					8						5
				f		(s)ds J3					[ f ]						f		(s0 )				f		(s1 )				f		(s2 ) ,
															18					18						18
		0
где s	0	1 0,6	,			s 1		,	s	2		1					0,6 .
		2		1			2								2

2m 2 )

(65)

121

Аналогично формуле Чебышева можно записать:

I N f b

f (x)dx

a

(66)

h

N

1

0,6

h

1

0,6

f

x

f

x

f

x

.

18

h

2

h

2

i 1

i

i

2

i

8.3. Оценки погрешности квадратурных формул

Существуют следующие оценки погрешности квадратурных формул

	N	b
DN ( f )	ci f (xi ) f (x)dx		, полученные на основе разложения интегри-
	i 0	a

руемой функции в ряд Тейлора, и оценки остаточного члена разложения. Для формулы прямоугольников

DN f h2	f ( )(b a) ; DN f h2	(b a)max f ( ) ;	(67)
24	24

здесь и далее – некоторая точка [a,b]; h – шаг интегрирования. Для формулы трапеций

DN f	h2		(68)
	12	f ( )(b a) .

Для формулы парабол (Симпсона)

DN f	b a	h4	f ( ) .	(69)
180

Очевидно, что точное значение интеграла в методе прямоугольников можно получить только при f (x) – кусочно-постоянной, а в методе

трапеций – при f (x) линейной или кусочно-линейной функции.

Пример 3 6 .
1	dx
Вычислить I 0		по формулам Ньютона – Лейбница, прямоуголь-
	1 x2

ников, трапеций и Симпсона с использованием средств MS Excel.

Решение.

Для заданной функции формула Ньютона – Лейбница имеет вид:

	1	dx		1
	0		arctgx		arctg1 arctg0.
		1 x2		0

Выполним вычисления в MS Excel.

1) Протабулируем функцию в диапазоне изменения значения аргумента 0 – 1 (рис. 31). В ячейке H2 зададим шаг.

122

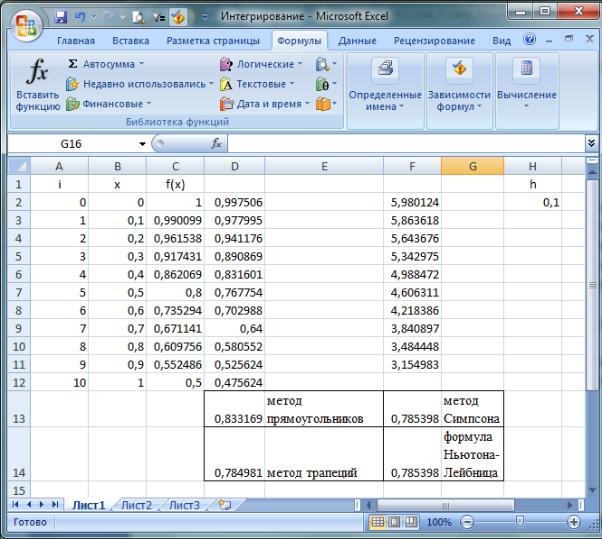
2)В ячейку D2 введем формулу вычисления частных сумм =1/(1+(B2+($H$2/2))^2), скопируем ее буксировкой до ячейки D12.

3)В ячейку D13 введем формулу метода прямоугольников (59):

=$H$2*СУММ(D2:D12).

4)В ячейку D14 введем формулу метода трапеций (60):

=$H$2/2*(C2+2*СУММ(C3:C11)+C12).

5)В ячейку F2 введем формулу вычисления частных сумм = C2+4*D2+C3, скопируем ее буксировкой до ячейки F11.

6)В ячейку F13 введем формулу метода Симпсона (61):

=$H$2/6*СУММ(F2:F11).

7) В ячейку F14 введем формулу Ньютона – Лейбница

= ATAN(B12)-ATAN(B2).

Сравнивая результаты вычислений, отметим, что наиболее точным оказался результат, полученный по формуле Симпсона.

Рис. 31. Пример численного интегрирования функции в MS Excel

123

Контрольные вопросы и задания

1.Какие формулы называются квадратурными?

2.Что такое шаблон квадратурной формулы?

3.Как получается определитель Вандермонда?

4.Сколько узлов содержит шаблон квадратурной формулы трапеций?

5.В какой квадратурной формуле число узлов должно быть нечетным?

6.В каком методе численного интегрирования исходят из оптимального выбора узлов интегрирования?

7. Вычислите интеграл I 2 sin xdx по формулам Котеса (62), Чебышева

0

(64) и Гаусса (66) в среде MS Excel и MathCAD.

124

при этом ( yi yi 1 ). Разности второго порядка:

yi yi 1 yiyi yi yi 1

yi 12 yi yi 12 yi 1 yi 1

9. РАЗНОСТНЫЕ УРАВНЕНИЯ

9.1. Сеточные функции

Как мы уже знаем, в приближенных методах функции непрерывного аргумента заменяются функциями дискретного аргумента – сеточными функциями. Сеточную функцию можно рассматривать как функцию целочисленного аргумента:

y i yi , i 0, 1, 2,

Для y i можно ввести операции, являющиеся дискретным (разност-

ным) аналогом операций дифференцирования и интегрирования. Аналогом первой производной являются разности первого порядка:

– правая разность,

– левая разность,

– центральная разность,

2 yi yi yi 2 2yi 1 yi ;yi yi 1 2yi yi 1 yi 2 yi 1 .

Аналогично определяется	разность m-го порядка m yi m 1 yi ,
содержащая значения yi , yi 1 , , yi m . Очевидно, что
i	i
y j yi 1 yk ; y j yi yk 1 .
j k	j k

9.1.1. Разностные аналоги формул дифференцирования произведения и интегрирования по частям

Пусть yi , vi	– произвольные функции целочисленного аргумента. Тогда
	yi vi yi vi vi 1 yi yi 1 vi vi yi ;				(70)
	yi vi yi 1 vi vi yi yi vi vi 1 yi .				(71)
Формулы	(70) и (71)	представляют	собой	аналоги	формулы
			yv vy	.
дифференцирования произведения y(x)v(x)
Аналогом формулы интегрирования по частям является формула
суммирования по частям:
	N 1	N
	yi vi	vi yi yN vN y0v0 .			(72)
	i 0	i 1

Действительно, поскольку yi yi 1 , из формулы (70) следует, что yi vi yi vi vi 1 yi yi vi vi 1 yi 1 ,

125

отсюда получаем:

N 1	N	N 1	N 1			N
yi vi vi yi yivi vi 1 yi 1 vi yi
i 0	i 1	i 0	i 0			i 1
		N	N
	yN vN y0v0 vi yi vi yi yN vN y0v0.
		i 1	i 1
Что и требовалось доказать.
Формулу (72) можно использовать для вычисления сумм.
Пример 3 7 .		N
Вычислить сумму SN i2i .
		i 1
						i
Положим vi i, yi 2i , так что yi yi 1 2i y0						2i	y0	2i 1 2.
						j 1
Выберем	y0 2 2N 1 ;	тогда	yN 0 .	Так	как	v0 0,	vi	1 ,	то из
формулы (72) следует, что
N	N 1	N 1			N 1			2N 1 2 ,
SN vi yi yi vi yi N y0 2 2i 1 N 2N 1
i 1	i 0	i 0			i 0
так что SN N 1 2N 1 2 .
	9.2. Разностные уравнения
Линейное	уравнение	относительно		сеточной		функции		yi	y i
i 0, 1, 2,
	a0 (i) y(i) a1 (i) y(i 1) am (i) y(i m) f (i),								(73)
где ak (i) (k 0,1, 2, , m),		f (i) –	заданные сеточные функции,
			a0 (i) 0,		am (i) 0,

называется линейным разностным уравнением m-го порядка.

Если использовать формулы конечных разностей, то можно уравне-

ние (73) переписать в виде:
a0 i yi a1	i yi am i m yi f i .	(74)

Есликоэффициенты a0 , a1 , , am независятотi, тоуравнение (73) назы-

вается разностным уравнением с постоянными коэффициентами.

	9.2.1. Уравнения первого порядка
При m 1	из уравнения (73) получаем разностное уравнение первого
порядка:	a0 i yi a1 i yi 1 f i ,	a0 i 0, a1 i 0	(75)
или	a0 i yi a1 i yi	f i , a0 a0 a1 .

126

Пример 3 8 .

Разностными уравнениями первого порядка являются формулы для

	вычисления			арифметической		и		геометрической		прогрессий:
	yi 1 yi d,			yi 1 qyi .					qi yi i , где qi a0 (i) ,
	Уравнение (74) можно переписать в виде yi 1
		f (i)								a1 (i)
	i		. Отсюда видно,		что решение			y(i) определено однозначно при
	i i0 ,	a1 (i)				y i0 .	Значения y1 , y2 , , yi , можно
		если		задано значение
	вычислить по формуле
					i		i 1	i		(76)
				yi 1	qk y0			qs	k i .
				k 0			k 0 s k 1

Для уравнения с постоянным коэффициентом формула примет вид:

i
yi 1 qi 1 y0 qi k k .		(77)
k 0
9.2.2. Уравнения второго порядка с постоянными коэффициентами
Рассмотрим разностное уравнение второго порядка
byi 1 cyi ayi 1 fi , i 1, 2, , a 0,	b 0,	(78)
коэффициенты которого не зависят от i.
Если fi 0 , то уравнение
byi 1 cyi ayi 1 0, i 1, 2,		(79)

называется однородным. Его решение может быть найдено в явном виде. Пусть yi , i 0,1, – решение однородного уравнения (79),

yi* , i 0,1, – какое-либо решение неоднородного уравнения (78). Тогда их сумма yi yi yi* также является решением неоднородного уравнения.

Действительно,	b yi 1 yi* 1 c yi 1 yi* 1 a yi 1 yi* 1
	byi 1 cyi ayi 1 byi* 1 cyi* ayi* 1 fi .

Это свойство – следствие линейности уравнения (75); оно сохраняет силу для разностного уравнения (73) любого порядка.

Очевидно, что если yi является решением однородного уравнения (79), то и cyi , где c – произвольная постоянная, также удовлетворяет данному уравнению.

Пусть yi1 и yi 2 – два решения уравнения (79). Они являются линейно независимыми, если равенство c1 yi1 c2 yi 2 0, i 0,1, 2, , что возможно только при c1 c2 0 , или если определитель системы

127

	(1)	(2)	0,
c1 yi		c2 yi
	(1)	(2)
				m 1, 2,
c1 yi m c2 yi m 0,

отличен от нуля для всех i, m . В частности,

	y(1)	y(2)
i,i 1	i	i	0.
	yi(1)1	yi(2)1

Принимаем без доказательства два утверждения.

1. Если решения yi1 и yi 2 уравнения (79) линейно независимы, то об-

щее решение однородного разностного уравнения (79) имеет вид yi0 c1 yi1 c2 yi 2 ,

где c1 , c2 – произвольные постоянные.

2. Общее решение неоднородного уравнения (78) можно представить в

виде	y		y0	y* c y 1 c			y 2 y* ,				(80)
		i				2
			i	i	1 i		i	i
где y*	– частное решение уравнения (78). Для определения c								и c	2	, как и в
i								1

случае дифференциальных уравнений, надо задать дополнительные условия – начальные или краевые.

9.2.3. Нахождение общего решения однородного разностного уравнения

Общее решение уравнения (80) можно найти явно. Для этого линейно независимые решения будем искать в виде yi qi , где q 0 – неизвестное

пока число. После подстановки

yk

qk

в уравнение (79)

получим

квадратное уравнение bq2 cq a 0, имеющее корни

q1

c c2 4ab

,

q2

c c2 4ab

.

(81)

2b

2b

В зависимости от значений дискриминанта D c2

4ab возможны три

случая.

1) D 0 ,

корни действительны и различны. Им соответствуют два

решения y 1 qk

и y 2 qk , которыелинейно независимы, таккакотличен

k

1

k

2

от нуля определитель

qk

qk 1

qk qk q

q 0.

k ,k 1

1

1

2

q2k

q2k 1

1 2

1

Общее решение уравнения (79) имеет вид

y

k

c qk c

qk .

(82)

1

1

2

2

128

2) D 0 , корни комплексно-сопряженные:

q

c j

D

, q

2

c j

D

,

1

2b

2b

где j – мнимая единица. Эти корни удобно представить в виде

q e j , q

2

e j ,

a , arctg

D

.

1

b

c

Линейно независимыми решениями являются не только функции

qk k e jk k cosk j sin k ,

1

k e jk k cosk j sin k ,

q2k

но и функции yk1 k

cos k ,

yk2 k sin k , линейная независимость

которых следует из линейной независимости функций sink

и cosk .

Общее решение уравнения (79) имеет вид

sin k .

y

k

k

c cosk c

2

(83)

1

3) D 0 , корни действительны и равны: q1 q2 2cb q0 .

Линейно независимыми являются решения
yk1 q0k ,			yk2 kq0k .						(84)
Общее решение уравнения (75) имеет вид
y	k	c qk	c kqk .						(85)
		1 0	2	0
Пример 3 9 .
Найти общее решение уравнения
yk 1 2 pyk yk 1 0,			a b 1,			c 2 p 0.
Решение.
Возможны три случая:
1) p 1.
Положим p cos ; тогда D 4 cos2 1 4sin 2 0. Линейно неза-
висимые решения имеют вид
yk1 cosk , yk2 sin k ;
2) p 1.
Положим p ch . Напомним, что ch					e	e	, sh	e e	. Тог-
						2		2
да получим для q квадратное уравнение				q2 2ch q 1 0; его дискри-
минант D 4 ch2 1 4sh2 ,		а корни имеют вид					q ch sh e .
							1,2

Линейно независимыми решениями являются функции yk1 ch k , yk2 sh k ;

129

	3) p 1.
	В этом случае q2			2q 1 0, q			1, линейно независимые решения
имеют вид						1,2
					yk1 1, yk2			k.
	Во всех трех случаях общее решение уравнения будет иметь вид
				y	k	c y 1	c	2	y 2 .
						1 k			k
	Пример 4 0 .
	Найти общее решение уравнения
	Решение.			yk 1 yk 6yk 1 2k 1.
	Найдем сначала общее решение однородного уравнения.
	D 1 24 25 0;			корни квадратного					уравнения q2 q 6 0 равны
q	3, q	2	2, так что y 1 3k ,			y 2 2 k .
1				k		k		c 2k , где c const . Подставив
	Частное решение находим в виде						yk*
значение yk* в исходное уравнение, получим:
			c 2k 1 2k 6 2k 1 c 2k 1 4 2k 1, c 1.
	Общее решение неоднородного уравнения представляет собой сумму
yi	yi yi* общего решения однородного уравнения и частного решения

неоднородного. Следовательно, общее решение будет иметь вид yk c1 3k c2 2 k 2k .

Контрольные вопросы и задания

1.Какой вид имеет линейное разностное уравнение m-го порядка?

2.От чего зависит порядок разностного уравнения?

3.Приведите примеры разностных уравнений первого порядка.

4.Какая функция называется сеточной? Приведите пример.

5.Что собой представляет сетка для построения дискретного аналога дифференциального уравнения?

6.Что является аналогом первой производной?

7.Какая формула является разностным аналогом формулы дифференцирования по частям, формулы интегрирования по частям?

8.Какие разностные уравнения называются однородными?

9.Как выглядит разностное уравнение первого порядка с постоянными коэффициентами?

10.Как вычисляются разности первого порядка: правая, левая, центральная разность?

11.Если общее решение неоднородного уравнения представлено в виде

суммы yi yi0 yi* , то чем являются каждое из этих слагаемых? 12. Найдите общее решение уравнения yk 1 yk 6yk 1 2k 1.

130