Розділ 4. Електричні коливання

§ 7. Електричні коливання

7.1. Квазістаціонарний струм

При розгляді коливань маємо справу з струмом, що змінюється в часі. Закони Ома, Кірхгофа залишаються справедливими лише для миттєвих значень струму і напруги, при умові, що їх зміна відбувається не достатньо швидко. Електромагнітні збурення поширюються по колу з швидкістю світла.

Нехай довжини кола чисельно дорівнює l і якщо за час , необхідний для передачі цього збурення у найвіддаленішу точку кола, сила струму змінюється незначно, то миттєве значення струму в усіх перерізах кола будуть однакові. І тоді струми, які задовольняють дану умову називаютьсяквазістаціонарними.

Для струмів, що періодично змінюються, умова квазістаціонарності має вигляд:

,

де Т – період даних змін.

7.2. Коливальний контур. Вільні коливання в контурі без активного опору

В колі, що має індуктивність і ємність, можуть виникати електричні коливання. Таке коло називається коливальним контуром.

Коливання в контурі можна викликати, надавши обкладкам конденсатора певний початковий заряд або збудивши в індуктивності струм (наприклад, шляхом вимкнення зовнішнього магнітного поля, що

пронизує витки котушки). Використаємо перший спосіб. Під’єднаємо відімкнений від індуктивності конденсатор до джерела напруги. Це призведе до виникнення на його обкладках різнойменних зарядів +q і –q (стадія1). Між обкладками виникає електричне коло, енергія якого . Якщо потім вимкнути джерело напруги і замкнути конденсатор на індуктивність ємність почне розряджатись і в контурі потече струм. В результаті енергія електричного поля буде зменшуватись, але виникне енергія магнітного поля, обумовленого струмом, що тече черезіндуктивність. Ця енергія рівна.

Рис.7.1

Оскільки активний опір контуру дорівнює нулю, повна енергія, що складається з енергії електричного і магнітного полів не витрачається на нагрівання і буде залишатись постійною. Тому в момент, коли напруга на конденсаторі, а відповідно – і енергія електричного поля обертається в 0, енергія магнітного поля, а отже і струм, досягають найбільшого значення (стадія 2; починаючи з цього моменту струм тече за рахунок ЕРС самоіндукції).

Надалі струм зменшується і коли заряди на обкладках досягнуть початкового значенняq, сила струму стане рівною нулю (стадія 3). Потім ті ж самі процеси протікають у зворотному напрямку (стадія 3, 5), після чого система приходить в початковий стан (стадія 5) і весь цикл повторюється знову і знову. В ході процесу періодично змінюються (тобто коливаються) заряд на обкладках, напруга на конденсаторі і сила струму, що тече через індуктивність. Коливання супроводжується взаємними перетворюваннями енергії електричного і магнітного полів.

Знайдемо рівняння коливань в контурі без активного опору. Будемо вважати позитивним струм, який заряджає конденсатор. Тоді

. (7.1.1)

Рис. 7.2

Запишемо для кола 1-3-2 (рис. 7.2) вираз закону Ома

. (7.1.2)

В нашому випадку R=0, , .Підстановка цих значень в (7.1.2) дає

. (7.1.3)

Замінивши dI/dt через отримаємо рівняння

. (7.1.4)

Якщо ввести позначення (7.1.5), рівняння (7.1.4) набуває вигляду

. (7.1.6)

Розв’язком цього рівняння є функція

. (7.1.7)

Таким чином, заряд на обкладках конденсатора змінюється по гармонічному закону з частотою, що визначається виразом (7.1.5). Ця частота називається власною частотою контуру (вона відповідає власній частоті гармонічного осцилятора). Для періоду коливань отримуємо, так звану, формулу Томсона:

. (7.1.8)

Напруга на конденсаторі відрізняється від заряду множником 1/С:

. (7.1.9)

Про диференціювавши функцію (7.1.7) по часу, отримаємо вираз для сили струму

. (7.1.10)

Таким чином, сила струму випереджає по фазі напругу на конденсаторі на .

Зіставлення формул (7.1.7) і (7.1.9) з формулою (7.1.10) показує, що в момент, коли струм досягає найбільшого значення, заряд і напруга обертаються в 0 і навпаки. Це співвідношення між зарядом і струмом також було встановлено з енергетичних міркувань.

З формул (7.1.9) і (7.1.10) слідує, що

, .

Взявши відношення цих амплітуд, отримаємо

. (7.1.11)

Цю формулу можна отримати також виходячи з того, що найбільше значення енергії електричного поля повинно дорівнювати найбільшому значенню енергії магнітного поля.

7.3. Вільні затухаючі коливання

Будь-який реальний контур володіє активним опором. Енергія, накопичена в контурі, поступово витрачається в цьому опорі на нагрівання, внаслідок чого вільні коливання затухають. Рівняння (7.1.2), записане для кола 1-3-2, зображеного на рис.6.3, має вигляд

. (7.2.1)

Розділимо це рівняння наL і замінивши І через , аdI/dt через , отримаємо

. (7.2.2)

Врахувавши (7.1.5) і позначивши

, (7.2.3)

рівнянню (7.2.2) можна надати вигляд

. (7.2.4)

Рис.7.3

Останнє рівняння співпадає з диференціальним рівнянням затухаючих механічних коливань.

За умови, що , розв’язок рівняння (7.2.4) має вигляд

, (7.2.5)

де .

. (7.2.6)

Таким чином, частота затухаючих коливань менше власної частоти. ПриR=0 вираз (7.2.6) переходить в (7.2.5).

Розділимо функцію (7.2.5) на ємність С і отримаємо напругу на конденсаторі:

. (7.2.7)

Щоб знайти силу струму необхідно про диференціювати (7.2.5) по часу:

.

.

.

Введемо кут , що визначається умовами

, .

Тоді можна записати:

. (7.2.8)

Оскільки , а, значеннялежить в межах віддо. Таким чином, при наявності в контурі активного опору сила струму випереджає по фазі напругу на конденсаторі на(приR=0 випередження складає ).

Графік функції (7.2.5) зображено на рис. 7.4. Графіки для напруги і сили струму мають аналогічний вигляд.

Затухання коливань прийнято характеризувати логарифмічним дикриментом затухання.

, (7.2.9)

де а(t)– амплітуда відповідної величини (q,Uчи I).

Рис. 7.4

Логарифмічний дикримент затухання обернений до числа коливань N_е, що здійснюються за час, протягом якого амплітуда зменшується в е раз:

.

Підставивши в (7.2.9) значення (7.2.3) отримаємо наступний вираз:

. (7.2.10)

Частота , а відповідно івизначається параметрами контуруL,C,R. Таким чином, логарифмічний дикримент затухання є характеристикою контуру.

Якщо затухання невелике , можна покласти в (7.2.10). Тоді

. (7.2.11)

Коливальний контур часто характеризують його добротністю, яка визначається як величина, обернено пропорційна логарифмічному дикрименту затухання:

. (7.2.12)

З рівняння (7.2.12) випливає, що добротність контуру тим вища, чим більше число коливань встигає здійснитися до того, як амплітуда зменшиться в е раз. У випадку слабкого затухання

. (7.2.13)

При слабкому затуханні добротність механічної коливальної системи дорівнює відношенню енергії, накопиченої в системі в даний момент, до зменшення цієї енергії за один період коливань. Покажемо, що це справедливо і для електричних коливань.

Амплітуда сили струму в контурі зменшується за законом . ЕнергіяW, накопичена в контурі, пропорційна квадрату амплітуди сили струму (або квадрату амплітуди напруги на конденсаторі); відповідно, W зменшується за законом . Відносне зменшення енергії за період дорівнює

.

При незначному затуханні (тобто за умови, що ) можнавважати приблизно рівним:

.

Замінивши логарифмічний дикримент затухання на добротність:

. (7.2.14)

7.4. Вимушені електричні коливання. Резонанс

Для того, щоб викликати вимушені коливання потрібно здійснювати на систему зовнішню періодично змінну дію. У випадку електричних коливань це можна здійснити, якщо увімкнути послідовно з елементами контуру змінну ЕРС або, розірвавши контур, подати на контакти, що утворилися змінну напругу (рис.7.5)

(7.3.1)

Рис.7.5

Цю напругу потрібно додати до ЕРС самоіндукції. В результаті формула (7.2.1) набуде вигляду

. (7.3.2)

Виконавши перетворення, отримаємо рівняння

. (7.3.3)

Рівняння (7.3.3) співпадає з рівнянням вимушених механічних коливань. Частинний розв’язок цього рівняння має вигляд

, (7.3.4)

де ,.

Підставимо значення і, тоді

, (7.3.5)

. (7.3.6)

Продиференціювавши рівняння (7.3.4) по часу, знайдемо силу струму а контурі при встановлених коливаннях:

.

Запишемо цей вираз у вигляді

, (7.3.7)

де – зсув по фазі між струмом і прикладеною напругою. Відповідно до (7.3.6)

. (7.3.8)

З цієї формули слідує, що струм відстає по фазі від напруги в тому випадку, коли і випереджає струм по фазі за умови, що. Згідно (7.3.5)

. (7.3.9)

Представимо співвідношення (7.3.2) у вигляді

. (7.3.10)

Добуток I_R дорівнює напрузі U_R на активному опорі, q/C є напругою на конденсаторі U_C, вираз L(dI/dt) визначає напругу на індуктивності U_L. З урахуванням цього можна записати

(7.3.11)

Таким чином, сума напруг на окремих елементах контуру дорівнює в кожний момент часу напрузі, прикладеній ззовні (рис.7.5).

Відповідно до (7.3.7)

(7.3.12)

Розділивши вираз (7.3.4) на ємність отримаємо напругу на конденсаторі

. (7.3.13)

. (7.3.14)

Помноживши похідну функції (7.3.7) на L, отримаємо напругу на індуктивності:

. (7.3.15)

. (7.3.16)

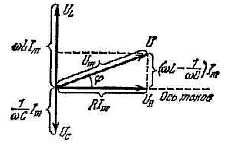
З наведених формул видно, що напруга на ємності відстає по фазі від сили струму на π/2, а напруга на індуктивності випереджає струм на π/2. Напруга на активному опорі змінюється у фазі зі струмом. Фазові співвідношення можна представити у вигляді векторної діаграми (рис. 7.6).

Резонансна частота для заряду q і напругу на конденсаторі U_C дорівнює

. (7.3.17)

Резонансні криві для U_Cзображені на рис.7.7 (резонансні криві для q мають такий же вигляд). При резонансні криві сходяться в одній точці з ординатоюU_Cm=U_m – напрузі, що виникає на конденсаторі при підключенні його до джерела постійного струму U_m. Максимум при резонансі виходить тим вищий і гостріший, чим менше β=R/2L, тобто чим менший активний опір і більша індуктивність контуру.

Резонансні криві для сили струму показані на рис. 7.8. Вони відповідають резонансним кривим для швидкості при механічних коливаннях. Амплітуда сили струму має максимальне значення при (з формули 6.3.9). Відповідно резонансна частота для сили струму співпадає з власною частотою контуру ω₀:

. (7.3.18)

Рис. 7.6

Відрізок, що відтинається резонансними кривими на осі І_m, дорівнює нулю – при постійній напрузі встановлений струм в колі з конденсатором протікати не може.

У випадку малого затухання (при β²<<ω₀²)резонансну частоту для напруги можна вважати рівною нулю. Відповідно можна вважати, що . Згідно формули (7.3.14) відношення амплітуди напруги на конденсаторі при резонансі до амплітуди зовнішньої напруги буде в цьому випадку дорівнювати

(7.3.19)

Тут Q–добротність контуру. Таким чином, добротність контуру показує, у скільки разів напруга на конденсаторі може перевищити прикладену до контуру напругу.

Добротність контуру визначає також гостроту резонансних кривих. Можна показати, що відношення широти резонансної кривої, взятої на висоті 0,7 до резонансної частоти дорівнює величині, оберненій до добротності контура:

. (7.3.20)

Формули (7.3.19) і (7.3.20) справедливі лише при великих значеннях Q, тобто у випадку, коли затухання вільних коливань в контурі мале.

Рис.7.7 Рис.7.8 Рис.7.9

Лекція 19