Сплайновые кривые.

Рассмотрение интерполяционных кривых, для описания пространственных линий, выявило два основных недостатка этих кривых. Если описываемая линия имеет сложный вид, то приходится на этой линии выбирать достаточно много опорных точек. Это приводит к тому, что порядок интерполяционной кривой может быть очень большим. Если, например, взять 100 опорных точек, то интерполяционная кривая будет полиномом степени 99. Отсюда возникают следующие проблемы.

Во-первых, возрастает сложность вычисления точек кривой. Во-вторых, несмотря на то, что кривая проходит через все опорные точки, отклонение от заданной линии в других точках может быть очень большим, как это видно на Рис.10.

Поэтому обычно следуют другим путем. Разбивают пространственную линию на отдельные небольшие сегменты. Каждый такой сегмент аппроксимируют параметрической кривой небольшого порядка, обычно кубической кривой. Причем, при выборе кривой не требуют, чтобы кривая точно проходила через опорные точки, довольствуясь прохождением кривой вблизи опорных точек. В месте стыковки двух соседних сегментов стараются обеспечить гладкость общей составной кривой.

То, что получается в результате описанной процедуры, называют сплайновой кривой. Таким образом, можно говорить об элементарных сплайновых кривых и составных сплайновых кривых.Элементарные сплайновые кривыеописывают отдельные сегменты пространственной линии.Составная сплайновая криваястроится из элементарных кривых и описывает пространственную линию целиком.

Сплайновые кривые Эрмита.

Сплайновая кривая Эрмита (Hermite) является кубической кривой и ищется в следующем виде:

(16)

Здесь параметр tменяется на интервале [0, 1], а неизвестные векторыопределяются из следующих условий.

Будем считать, что кривая Эрмита начинается в точке с опорным вектором , а кончается в точке с опорным вектором. Это приводит к следующим условиям:

(17)

Далее возьмем первую производную от радиуса-вектора (16) по параметру t.

(18)

Будем считать, что известны векторы производных (касательные векторы) в начале и конце кривой. Это приведет к следующим условиям:

(19)

Далее подставляя (16) в (17), а (18) в (19) найдем неизвестные векторы .

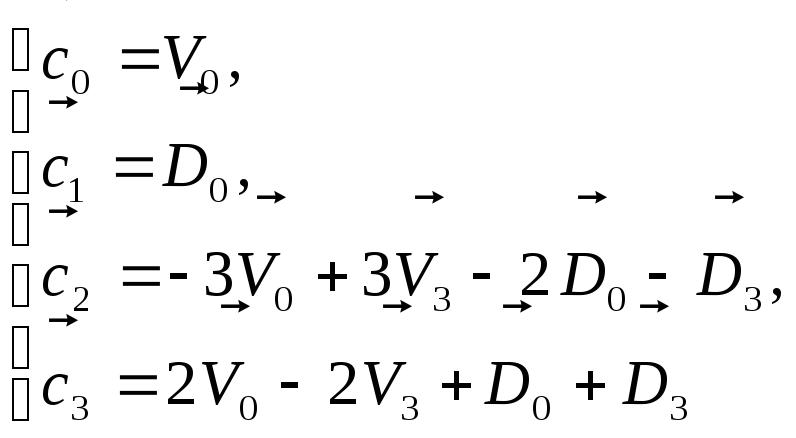(20)

В компьютерной графике удобно многие математические выражения записывать в матричном виде. Поэтому введем два столбца, элементами которых будут трехмерные векторы.

(21)

Тогда систему уравнений (20) можно записать в виде одного матричного уравнения.

(22)

Здесь матрица M_Hназывается матрицей Эрмита (Hermitematrix) и имеет следующий вид:

(23)

Если, кроме того, ввести столбец, элементами которого являются разные степени параметра t,

, (24)

то уравнение кривой Эрмита можно тоже представить в виде матричного уравнения.

(25)

Здесь значок Tозначает транспонирование. В развернутом виде уравнение (25) имеет следующий вид:

(26)

На Рис.11. показана элементарная кривая Эрмита, построенная с помощью формулы (26).

Рис.11. Элементарная кривая Эрмита. Опорные точки V0,V3. Касательные векторыD0,D3.

Рис.12. Составная кривая Эрмита составлена из трех элементарных кривых Эрмита. Опорные точки V0,V3,V6,V9. Касательные векторыD0,D3,D6,D9.

(Изображение на Рис.11 создано программой line5.cpp, на Рис.12 создано line6.cpp.)

Чтобы получить гладкую составную сплайновую кривую Эрмита, нужно обеспечить плавный переход в точках стыковки отдельных элементарных сплайновых кривых. Это обеспечивается выбором одного касательного вектора для двух соседних элементарных сплайновых кривых.

На Рис.12. показана гладкая составная сплайновая кривая Эрмита, состоящая из трех элементарных сплайновых кривых. Для задания этой кривой понадобилось 8 векторов – четыре опорных вектора V₀,V₃,V₆,V₉и четыре касательных вектораD₀,D₃,D₆,D₉.

Для аппроксимации заданной линии составной сплайновой кривой Эрмита, поступают следующим образом. Помещают опорные точки на заданную линию, и затем подбирают касательные векторы, так чтобы достичь нужной точности аппроксимации. На практике оперировать касательными векторами не всегда удобно.

Поэтому существуют другие сплайновые кривые, где используются только опорные векторы. К таким сплайновым кривым относятся сплайновые кривые Безье и B-сплайновые кривые.