Нормализованные базисные функции b-сплайна.

Построение составной B-сплайновой кривой из элементарных кубическихB-сплайновых кривых не составляет большого труда. Однако чтобы сделать построение составной сплайновой кривой более удобным и быстрым, были придуманы другие подходы к этой проблеме.

Посмотрим, как можно построить составную B-сплайновую кривую, используя нормализованные базисные функцииB-сплайна.

Если заданы N+1 опорные векторыV₀,V₁,,V_N-1,V_N, то уравнение сплайновой кривой будем искать в следующем виде:

(50)

Здесь N_m,i(t)– нормализованные базисные функцииB-сплайна,m-порядок сплайновой кривой. Нормализованные базисные функции обычно строят с помощью рекурсивной процедуры Кокса-де Бура (Cox-deBoorrecursion).

При построении базисных функций вводят узловой вектор (NodalVector). Узловой вектор – это упорядоченный массив чисел {t_i}. Основным свойством элементов этого вектора является монотонное нарастание величины элементов.

Размерность Kузлового вектора определяется числом опорных векторовN+1 и порядком базисных функцийm, и равнаK=N+m+ 2. В этом случае узловой вектор выглядит следующим образом:

(51)

Параметр базисных функций tменяется в некотором заданном интервале.

(52)

Меняя узловой вектор (51) и интервал (52) изменения параметра tможно получать сплайновые кривые с разными заданными свойствами.

Рекурсивная формула Кокса-де Бура имеет следующий вид:

(53)

При использовании формул (53) следует считать, что 0/0 = 0.

Если узлы{t_i} в узловом векторе (51) расположены равномерно, то соответствующий сплайн называетсяравномернымB-сплайном (UniformSpline), если же нет, то называетсянеравномернымB-сплайном (NonuniformSpline). Если узлы расположены равномерно и, кроме того, концевые узлы являются кратными с кратностьюm+1, то сплайн называетсяоткрытымB-сплайном (OpenSpline).

Для примера посмотрим как с помощью формул (50), (51), (53) можно описать элементарных кубический B-сплайн, рассмотренный ранее с помощью формул (38) и (39).

Возьмем четыре опорных вектора V₀,V₁,V₂,V₃, это означает чтоN=3. Рассматриваем кубические сплайны, поэтому порядок сплайна равенm=3. В результате получаем размерность узлового вектораK=N+m+ 2 = 8. Будем рассматривать равномерныйB-сплайн, с узловым вектором следующего вида:

(54)

Другими словами, в формулу (53) надо подставлять следующие значения узлов:

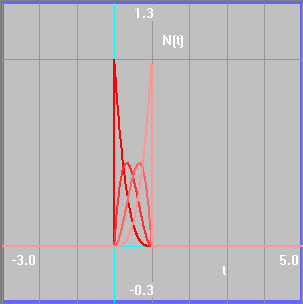
Теперь используя вектор узлов (54) и рекурсивные формулы (53), можно получить четыре базисные функции N_3,0(t),N_3,1(t),N_3,2(t),N_3,3(t).

На Рис.27 показаны графики этих четырех функций.

Рис.27 Четыре нормализованные кубические базисные функции для узлового вектора [-3 –2 –1 0 1 2 3 4].

Рис.28 Четыре нормализованные кубические базисные функции для узлового вектора [0 0 0 0 1 1 1 1].

(Изображения на Рис. 27, 28 созданы программой line11.cpp.)

На Рис.27 следует обратить внимание на то, что для построения одной кубической базисной функции необходимо использовать 5 узлов узлового вектора (54). Поэтому для четырех сдвинутых базисных функций требуется 8 узлов. Отсюда получаем размерность узлового вектора.

Далее, чтобы получить знакомую элементарную кубическую B-сплайновую кривую, интервал изменения параметра (52) надо выбрать следующим.

(55)

На Рис.29 показана сплайновая кривая, полученная с помощью узлового вектора (54) и условия (55).

Рис.29 Кубическая B-сплайновая кривая, построенная с помощью указанного вектора узлов.

Рис.30 Кубическая B-сплайновая кривая, построенная с помощью указанного вектора узлов.

(Изображения на Рис. 29, 30 созданы программой line12.cpp.)

На Рис.29 показана сплайновая кривая, в точности совпадающая с элементарной кубической B-сплайновой кривой, приведенной на Рис.22.

Теперь поэкспериментируем с узловым вектором (54), и сделаем крайние узлы кратными, как показано ниже:

(56)

На Рис.28 показано, как изменились в этом случае нормализованные базисные функции.

Если вспомнить формулы (30) для кубических функций Безье, то обнаружится, что графики на Рис.28 в точности совпадают с графиками для функций Безье. Поэтому следует ожидать, что сплайновая кривая, построенная с вектором узлов (56) будет совпадать с элементарной кубической кривой Безье.

Возьмем узловой вектор (56) и в интервале изменения параметра (55) построим сплайновую кривую. На Рис.30 показан результат построения этой сплайновой кривой.

На Рис.30 показана кривая, обладающая всеми свойствами кривой Безье. Таким образом, использование нормализованных базисных функций (53) при соответствующем выборе узлового вектора (51), можно получить как элементарную кубическую B-сплайновую кривую, так и элементарную кубическую кривую Безье.

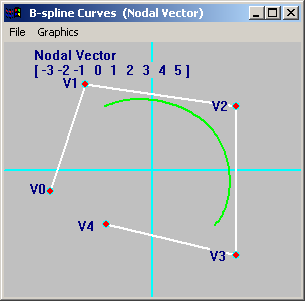
Построим составнуюB-сплайновую кривую, состоящую из двух элементарныхB-сплайновых кривых. Для этого выберем 5 опорных векторовV₀,V₁,V₂,V₃,V₄. В качестве узлового вектора возьмем следующий вектор:

(57)

Интервал изменения параметра tвыбираем следующим.

(58)

На Рис.31 показана сплайновая кривая, полученная с помощью узлового вектора (57) и интервала изменения параметра (58).

Рис.31 Равномерная сплайновая кривая.

Рис.32 Открытая сплайновая кривая.

(Изображения на Рис. 31, 32 созданы программой line12.cpp.)

На Рис.31 показана сплайновая кривая, в точности совпадающая с составной кубической B-сплайновой кривой, приведенной на Рис.23.

Посмотрим, как можно зафиксировать концы составной B-сплайновой кривой. Возьмем 10 опорных векторов:

В качестве узлового вектора возьмем следующий вектор:

(59)

Интервал изменения параметра tвыбираем следующим.

(60)

На Рис.32 показана открытая сплайновая кривая, полученная с помощью узлового вектора (59) и интервала изменения параметра (60). Сравним эту кривую с кривой, приведенной на Рис.24. В центральной части кривые совпадают, а на концах имеются отличия.

Составная B-сплайновая кривая, приведенная на Рис.24 составлена из 7 элементарных кубическихB-сплайновых кривых. Закрепление кривой на концах выполнено с помощью нужного выбора концевых опорных векторов. В результате кривая оказалась проходящей через опорные точкиV₁, иV₈

Открытая B-сплайновая кривая, приведенная на Рис.32 получена с помощью 10-ти нормализованных базисных функцийB-сплайна. В качестве узлового вектора был выбран вектор (59). В результате, кривая оказалась проходящей через опорные точкиV₀, иV₉.

В заключение приведем построение равномерной квадратичной B-сплайновой кривой Рис 32a. В качестве узлового вектора возьмем следующий вектор. Интервал изменения параметраtвыбираем следующим.

Рис.32a

Равномерная квадратичная B-сплайновая кривая.

(Изображение на Рис. 26 создано программой norm01.cpp.)

Покажем так же построение открытой квадратичной B-сплайновой кривой Рис 32b. В качестве узлового вектора возьмем следующий вектор. Интервал изменения параметраtвыбираем следующим.

Рис.32a

Равномерная квадратичная B-сплайновая кривая.

(Изображение на Рис. 26 создано программой norm01.cpp.)