4 Вопрос Классификация магнитных материалов.

Применяемые в электронной технике магнитные материалы подразделяют на две основные группы: магнитотвердые и магнитомягкие. В отдельную группу выделяют материалы специального назначения.

К магнитотвердым относят материалы с большой коэрцитивной силой Нс. Они перемагничиваются лишь в очень сильных магнитных полях и служат для изготовления постоянных магнитов.

К магнитомягким относят материалы с малой коэрцитивной силой и высокой магнитной проницаемостью. Они обладают способностью намагничиваться до насыщения в слабых магнитных полях, характеризуются узкой петлей гистерезиса и малыми потерями на перемагничивание. Магнитомягкие материалы используются в основном в качестве различных магнитопроводов: сердечников дросселей, трансформаторов, электромагнитов, магнитных систем электроизмерительных приборов и т. п.

Условно магнитомягкими считают материалы, у которых Нс< 800 А/м, а магнитотвердыми - с Нс> 4 кА/м. Необходимо, однако, отметить, что у лучших магнитомягких материалов коэрцитивная сила может составлять менее 1 А/м, а лучших магнитотвердых материалах ее значение превышает 500 кА/м. По масштабам применения в электронной технике среди материалов специального назначения следует выделить материалы с прямоугольной петлей гистерезиса (ППГ), ферриты для устройств сверхвысокочастотного диапазона и магнитострикционные материалы.

Внутри каждой группы деление магнитных материалов по родам и видам отражает различия в их строении и химическом составе, учитывает технологические особенности и некоторые специфические свойства.

Свойства магнитных материалов определяются формой кривой намагничивания и петли гистерезиса. Магнитомягкие материалы применяются для получения больших значений магнитного потока. Величина магнитного потока ограничена магнитным насыщением материала, а потому основным требованием к магнитным материалам сильноточной электротехники и электроники является высокая индукция насыщения. Свойства магнитных материалов зависят от их химического состава, от чистоты используемого исходного сырья и технологии производства. В зависимости от исходного сырья и технологии производства магнитомягкие материалы делятся на три группы: монолитные металлические материалы, порошковые металлические материалы (магнитодиэлектрические) и оксидные магнитные материалы, кратко называемые ферритами.

5 Вопрос Система уравнений Максвелла. Граничные условия

§ 2. Система уравнений Максвелла — основа электродинамики

2.1. Уравнения Максвелла для системы зарядов в вакууме.

Впервые полная система уравнений была записана Д. К. Максвел­лом в виде уравнений поля в веществе (см. § 15, п. 15.3). В математи­ческом отношении уравнения поля для вакуума являются частными случаями уравнений поля для вещества (µ = е = 1). Однако в физиче­ском плане уравнения в вакууме играют более фундаментальную роль. Как исходная система уравнений Максвелла для элементарных зарядов в пустоте впервые применена X. А. Лоренцом в 1903 г. Совре­менный вид уравнения Максвелла, используемые нами ниже, при­обрели в работах Г. Герца и О. Хэвисайда в конце прошлого века.

По отношению ко всему учению об электромагнитном поле си­стема уравнений Максвелла играет роль первоначальных исходных положений, или теоретических принципов. С исторической точки зрения она является абстрактным обобщением экспериментальных данных, и ее связь с эмпирическими законами электродинамики будет показана далее. Сейчас выпишем уравнения без обсуждения их происхождения и истории открытия, т. е. в готовом виде:

(2.1 - a)

(2.1 - б)

(2.1 - в)

(2.1 - г)

В уравнения входят следующие константы:

— магнитная постоянная;

= 8,85 • 10^-12—электрическая постоянная.

Они появились здесь вследствие выбора единиц измерения величин и, с одной стороны иρи с другой, независимо от их связи, ука­зываемой уравнениями.

Прямым расчетом можно убедиться, что

(2.2)

где с = 3 • 10⁸ м/с — константа, равная скорости света в вакууме. Далее будет показано, что формула (2.2) отражает не случайное совпаде­ние, а константа с имеет глубокую связь с уравнениями.

Используя равенство (2.2), уравнения Максвелла можно перепи­сать в следующей эквивалентной форме:

(2.3 - а)

(2.3 - б)

(2.3 - в )

(2.3 – г )

Уравнения (2.1) или (2.3) устанавливают связь между векторами ЕиВ поля, плотностью заряда и плотностью тока в каждой точке про­странства в любой момент времени. Таков общий смысл любых диф­ференциальных уравнений в частных производных по координатам точки пространства и по времени. Все переменные величины, входя­щие в уравненияматематически есть функции четырех независимых переменных: трех пространственных координат и времени.

Частные производные в уравнениях имеют обычный смысл: при дифференцировании по одной из переменных остальные считаются постоянными. Частное дифференцирование по времени означает, что поле и заряд рассматриваются в неподвижной точке про­странства. (Так как заряды движутся, важно помнить, что их плот­ность ρ и величина ρdVнаходятся именно в неподвижной точке для неподвижного объема dV.)

Уравнения Максвелла (2.1) или (2.3) непосредственно при­менимы при изучении макроскопических потоков элементарных частиц или ионов в пустоте (например, электронные пучки, плазма и т. д.). Вообще говоря, их нельзя использовать, если система электри­ческих зарядов расположена на телах, токи движутся по проводни­кам, а не непосредственно в вакууме, так как вещество существенно влияет на электромагнитное поле, на плотности токов и зарядов. Однако и при наличии тел возникает возможность непосредствен­ного применения уравнений (2.1). В ряде очень важных случаев тела, которые определяют расположение и движение зарядов, сами не влияют на поле. Так, например, поле малых по размерам заряжен­ных тел в воздухе рассчитывается как поле системы зарядов в вакууме; магнитное поле линейного проводника с током —как поле соответствующего тока в вакууме и т. д.

Уравнения Максвелла разделены на две пары для того, чтобы под­черкнуть наличие связей между отдельными уравнениями: второе уравнение в каждой паре следует из первого. Покажем это.

Возьмем дивергенцию от обеих частей уравнения (2.1-а):

Или

Следовательно, всегда постоянна во времени. Но постоянная во времени дивергенция от произвольного переменного поля может быть только нулем. Значит,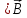= 0, что уже отражено в уравнении(2.1-6).

Точно так же, вычислив дивергенцию от обеих частей уравнения (2.1-в), имеем

(2.4)

откуда с помощью уравнения непрерывности (1.6) получаем уравне­ние (2.1-г).

При другом подходе к системе (2.1) можно не считать уравнение непрерывности (1.6) отдельным и независимым постулатом теории электричества. Его можно получить из уравнений Максвелла. Для этого подставим в равенство (2.4) , взятую из уравнения (2.1-г). Получаем закон сохранения заряда в дифференциальной форме:

Как известно, имеется глубокая связь законов сохранения важнейших физических величин с симметриями пространства-времени (или иными симметриями). «Правиль­ные» уравнения движения материальных тел или полей в любой фундаментальной физической теории (в механике, электродинамике и т д.) содержат в себе законы сохранения энергии, импульса, момента импульса, заряда и других физических вели­чин В этом плане существенно важно то, что закон сохранения заряда вытекает из уравнений Максвелла. (Этот закон связан с так называемой калибровочной инва­риантностью основных уравнений электродинамики ) Но сам закон шире рамок клас­сической электродинамики; как показывает опыт, он справедлив для всех взаимодей­ствий в природе. Поэтому к системе уравнений (2.1) обычно добавляется пятое соотно­шение; уравнение непрерывности (1.6). В таком случае только два из уравнений (2.1) можно считать независимыми —(2.1-а) и (2 1-в)

Заметим, что в физике не стремятся использовать непременно минимальную си­стему исходных положений. Если отношения между уравнениями выяснены, то обычно применяется несколько избыточная, но достаточно удобная и физически содержательная система. В электродинамике используются все четыре уравнения (2.1). Зависимые уравнения (2.1-6) и (2.1-г) несут важную физическую информацию и непо­средственно применяются в ряде задач. Так, соотношение = 0 истолковывается следующим образом, не существует в природе магнитных зарядов Q_M, создающих магнитное поле подобно тому, как электрические заряды Q создают электрическое поле.

Здесь следует сделать небольшое отступление. Как известно, элементарные магнит­ные диполи существуют' многие элементарные частицы (электроны, протоны, ней­троны и др.) обладают собственным магнитным моментом, называемым спиновым. Он не зависит от движения частицы в пространстве. Однако «монополей», т. е. поло­жительных и отрицательных магнитных зарядов, которые образовали бы поле позакону=, не обнаружено, несмотря на специально поставленные многочисленные и разнообразные эксперименты.

Граничные условия

Для решения уравнений Максвелла, как в интегральной, так и в дифференциальной форме, необ­ходимо задать граничные, а при необходимости и начальные условия (для нестационарных задач).

В дальнейшем для построения математической модели электромагнитного поля нам необходимо рассматривать граничные условия на искомые функции. Очевидно (с учетом сделанных выше заме­чаний), что для адекватного описания граничных условий нам необходимо воспользоваться разде­лением источников на связанные и свободные и установить соотношения между полями связанных и свободных зарядов. Эти соотношения определяются свойствами вещества, в котором проявляют себя связанные заряды.

Рассмотрим случай, когда граничной поверхностью служит поверхность раздела двух сред с различными значениями диэлектрической проницаемости.

Рис. 1. Схема для вывода граничных условий: о — для вектора индукции D, б— для вектора напряженности Е.

На рис. 1а приведена схема для вывода граничных условий для нормальных компонент вектора Dв точке поверхности раздела сред. Здесь D₁и D2 — значения электрической индукции в средах 1 и 2 соответственно, ΔA — малая площадка на поверхности раздела сред, содержащая исследуемую точку. На этой площадке построим цилиндр с основаниями, параллельными границе раздела и лежащими в средах 1 и 2 соответственно. Высота цилиндра равна h.На рис. 1б приведена схема для вывода граничных условий для тангенциальных компонент вектора напряженности электрического поля Е. Здесь E₁и Е₂ — значения вектора напряженности электрического поля в средах 1 и 2 соответственно, L— малый контур, со сторонами, лежащими в средах 1 и 2. Применим равенство (18) для цилиндра, изображенного на рис. 1а. Интеграл в левой части равенства (18) представим в виде суммы трех интегралов (по двум основаниям цилиндра и по боковой стороне цилиндра). Заряд q,охваченный поверхностью цилиндра, вычислим по формуле , где— плотность свободных зарядов на поверхности раздела. Воспользуемся теоремой о среднем и устремимhк нулю, стягивая одновременно площадку к исследуемой точке поверхности раздела. В результате из уравнения (18) следует

(19)

где n — единичный вектор, нормальный поверхности раздела в точке, где наблюдаются вектора D₁и D2. Полагая ,и учитывая формулу (17), получим

(20)

Если применить равенство (8) к замкнутому контуру на рис. 2б и устремить короткие стороны к нулю ("толщина"слоя стремится к нулю), то получим

Е₂ • dl— E₁• dl = 0.

Так как dl/dl= 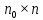(— единичный вектор, нормальный к нашему контуру (смотри рис. 2б), то

Поскольку данное соотношение справедливо при любой ориентации контура, то окончательно по­лучаем

(21)

т.е. тангенциальные составляющие вектора Е одинаковы по обе стороны границы раздела. Выразим поля через потенциалы:

(22)

Замечание 2. В случае не статических полей, когда rotE≠ 0, тангенциальная составляющая терпит разрыв на границе раздела двух сред. Об этом, в частности, следует помнить при решении задач распространения электромагнитных волн в волноводах.

Из уравнения (22) можно сделать заключение, что. Кроме того, нормальная компонента векторанепрерывна, если на поверхности раздела нет особенности в виде заряженного слоя.