2.1.8. Задача о секторах

Задан круг, разделенный на секторы. Даны три числа: k (0<=k<=20), n (n<=6) и m (m<=20), где n - количество секторов. В каждый из секторов помещается одно число >= k. Когда секторы заполнены числами, Вы можете получать из них новые числа по одному из следующих правил:

• взять число из одного сектора;

• взять число, равное сумме двух или более чисел в смежных секторах.

Из этих чисел составляется наибольшая последовательность подряд идущих новых чисел, начинающихся с числа m :(m, m+1, m+2, ..., i).

Напишите программу, которая определяет способ расстановки чисел в секторах, максимизирующий длину последовательности.

Пример. На рисунке показано, как получаются все новые числа от 2 до 21 из чисел, записанных в секторах. Серым цветом выделены суммируемые числа.

Входные и выходные данные

Исходные данные расположены во входном файле с именем INPUT.TXT, который содержит числа n, m и k. Ниже приведен пример файла исходных данных INPUT.TXT.

5

2

1

Выходной файл с именем OUTPUT.TXT должен содержать:

• наибольшее число i в неразрывной последовательности, которое может быть получено из чисел в секторах;

• все наборы чисел в секторах, из которых можно получить неразрывную последовательность от m до i. В каждой строке выводится один набор чисел в секторах. Каждый такой набор - список чисел, начинающихся с наименьшего ( которое может быть не единственным).

Например, (2 10 3 1 5) не является решением, так как начинается не с наименьшего числа. Обратите внимание, что (1 3 10 2 5) и (1 5 2 10 3) считаются различными решениями и должны быть оба выведены. Ниже приведен файл OUTPUT.TXT для нашего примера.

21

1 3 10 2 5

1 5 2 10 3

2 4 9 3 5

2 5 3 9 4

Если наименьшее число встретится несколько раз, вывести все возможные комбинации, например: (1 1 2 3), (1 2 3 1), (1 3 2 1) и (1 1 3 2).

Рассуждения по поводу задачи. Очевидно, что в первый сектор может помещаться число из интервала от k до m. Считаем, что минимальное из чисел находится в первом секторе. Если k больше m, то задача не имеет решения. Обозначим через Up верхнюю границу, а через Down - нижнюю границу интервала, из которого могут браться числа для записи в сектора с номерами от 2 до n. Общая схема («набросок»).

for l:=k to m do begin

<выбор числа в первый сектор>;

for j:=2 to n do begin (* j - номер сектора *)

<определение значений верхней и нижней границ для чисел, записываемых в сектор с номером j>;

for i:=Down to Up do (* i - записываемое число *)

begin

< записать в сектор с номером j число i >

< откорректировать массив сумм, которые можно составить из чисел, записанных в сектора>

< выполнить проверку последовательности сумм >

end;

end;

end;

Эта привлекательная схема перебора мало пригодна для «жизни», ибо время перебора будет весьма не привлекательным. Попробуем на этапе уточнения повысить пригодность схемы. "Откорректировать массив сумм". Пусть в Q (array[1..n,0..n] of byte) будут храниться суммы чисел из секторов круга S (array[1..n] of byte). В нулевом столбце элементы равны 0. В 1-м столбце - суммы, составленные из чисел, взятых из одного сектора, 2-м - из двух и т.д. В n-м столбце подсчитывается только элемент в первой строке.

Массив Q:

		1	2	3	4		5		6
1	0	S[1]	Q[1,1]+S[2]	Q[1,2]+S[3]	Q[1,3]+S[4]		Q[1,4]+S[5]		Q[1,5]+S[6]
2	0	S[2]	Q[2,1]+S[3]	Q[2,2]+S[4]		Q[2,3]+S[5]	Q[2,4]+S[6]
3	0	S[3]	Q[3,1]+S[4]	Q[3,2]+S[5]		Q[3,3]+S[6]	Q[3,4]+S[1]
4	0	S[4]	Q[4,1]+S[5]	Q[4,2]+S[6]		Q[4,3]+S[1]	Q[4,4]+S[2]
5	0	S[5]	Q[5,1]+S[6]	Q[5,2]+S[1]		Q[5,3]+S[2]	Q[5,4]+S[3]
6	0	S[6]	Q[6,1]+S[1]	Q[6,2]+S[2]		Q[6,3]+S[3]	Q[6,4]+S[4]

Итак, если у нас есть массив констант (для простоты) Sq вида

1 2 3 4 5 6

2 3 4 5 6 0

3 4 5 6 1 0

5 6 1 2 3 0

6 1 2 3 4 0,

то элемент массива Q[i,j] вычисляется следующим образом: Q[i,j]:=Q[i,j-1] + Q[Sq[i,j],1] .

При изменении числа в секторе с номером t необходимо откорректировать часть матрицы Q, показанную на рисунке темным цветом (эта часть больше, чем требуется, но для простоты считаем ее такой).

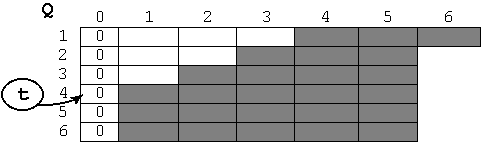
Схема процедуры уточнения сумм:

procedure AddSum(t,number :byte);

(* Q, Sq - глобальные переменные *)

var z,i,j :integer;

begin

Q[t,1]:=number;

for i:=1 to n do begin

if t-i+1>1 then z:=t-i+1 else z:=2;

for j:=z to n-1 do begin

Q[i,j]:=0;

Q[i,j]:=Q[i,j-1]+Q[Sq[i,j],1];

end;

end;

Q[1,n]:=Q[1,5] + Q[n,1];

end;

Следующее уточнение. "Выполнить проверку последовательности сумм". Из чего следует исходить? Во-первых, наилучшая последовательность сумм может получиться не из одного варианта заполнения секторов числами. Поэтому необходимо ввести структуру данных - двумерный массив - для их хранения и, соответственно, указатель числа записанных вариантов:

,

где type SView = array[1..nMax] of byte;

NumS :byte;

Во-вторых, для хранения наибольшего числа необходима переменная MaxS. В-третьих, значения сумм лучше представить множественным типом данных SetS :set of byte. Это упростит логику поиска последовательности. Процедура проверки имеет вид:

procedure Check;

(* SetS, BestS, NumS, MaxS, M - глобальные *)

var i,j :integer;

begin

SetS:=[];

for i:=1 to N do

for j:=1 to N-1 do SetS:=Sets+[Q[i,j]];

SetS:=SetS+[Q[1,N]];

i:=M;

while i in SetS do Inc(i);

if i>MaxS then begin

NumS:=1;

BestS[NumS]:=S;

MaxS:=i;(* на единицу больше действительной длины *)

end

else if i=MaxS then begin Inc(NumS); BestS[NumS]:=S; end;

end;

Общая схема уточнена. Но если довести ее до программы, то решение, например, для исходных данных n=6, m=1, k=1 за реальное время не будет получено. Необходимо сокращать перебор, искать эвристики, позволяющие сделать это.

1-я эвристика. Пусть у нас есть (n-1) сектор, в которые записаны числа, образующие последовательность m, m+1, ... . количество сумм (арифметическая прогрессия) равно n*(n-1)div2, т. е. это количество различных чисел, получаемое из чисел в заполненных n-1 секторе. Обозначим через X первое число из последовательности m, m+1, ..., которое мы не можем получить. В пустой сектор не имеет смысла записывать число, большее X. Поскольку X не превосходит n(n-1) div 2 + m, то это выражение можно считать значением верхней границы Up чисел, записываемых в сектора. В качестве нижней границы Down следует брать S[1], ибо числа, записываемые в сектора 2, 3, ..., n не меньше этого числа.

2-я эвристика. Пусть m<2*k. Тогда числа m, m+1, ..., 2*k-1 как сумма чисел из нескольких (более одного) секторов. Следовательно, либо, если 2*k-mn, все они должны находиться в круге, либо, если 2*k-m>n, в круге должны находиться числа m, m+1, ..., m+n-1.

3-я эвристика. "Исключение симметричных решений". При поиске числа для записи в последний сектор значение Down можно уточнить:

if < сектор последний > then Down:=S[2]

else Down:=S[1];

4-я эвристика. "Отсечение снизу". При поиске числа для последнего сектора нам известна максимальная сумма, которую дают числа, записанные в (N-1) сектор. Это значение Q[1,N-1]. Если сумма Up и Q[i,N-1] меньше ранее полученного наибольшего числа MaxS, то эту "ветку" в переборе вариантов можно "отсечь"(при любом варианте заполнения последнего сектора лучшего решения мы не получим).

Описанных эвристик (чем не эвристическое программирование?) оказывается достаточно для написания работоспособной программы для нижеприведенных тестов. В таблице приведены и правильные результаты.

N 3	M 1	K 1	max 7	1 2 4; 1 4 2
4	2	2	13	2 3 4 6; 2 6 4 3
5	3	1	22	3 5 7 4 6; 3 6 4 7 5
4	16	1	23	1 16 2 20; 1 20 2 16; 1 16 4 18; 1 18 4 16; 2 16 4 17; 2 17 4 16
5	16	12	20	16 17 18 19 20; 16 20 19 18 17; 16 17 18 20 19; 16 19 20 18 17; 16 17 19 18 20; 16 20 18 19 17; 16 17 19 18 20; 16 20 18 19 17; 16 17 19 20 18; 16 18 20 19 17; 16 17 20 18 19; 16 19 18 20 17 . . .
6	1	1	31	1 2 5 4 6 13; 1 13 6 4 5 2; 1 2 7 4 12 5; 1 5 12 4 7 2; 1 3 2 7 8 10; 1 10 8 7 2 3; 1 3 6 2 5 14; 1 14 5 2 6 3; 1 7 3 2 4 14; 1 14 4 2 3 7
6	2	2	29	2 3 7 4 9 6; 2 6 9 4 7 3
6	4	4	31	4 4 6 5 7 9; 4 9 7 5 6 4; 4 4 9 7 5 6; 4 6 5 7 9 4; 4 5 5 6 7 8; 4 8 7 6 5 5

57