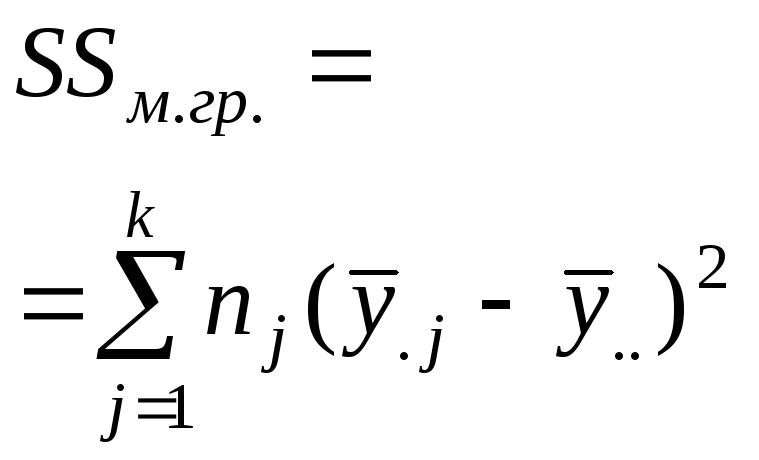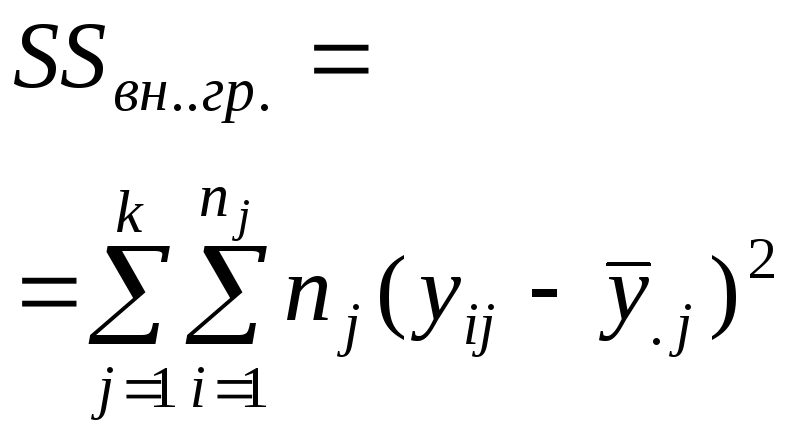Тема 6. Однофакторный дисперсионный анализ § 6.1. Постановка задачи

Сравнение двух средних значений нормально распределенных генеральных совокупностей (см. тема 3) может быть распространено на произвольное число средних значений.

Пусть имеется групп независимых наблюдений, образованных различными значениями признака классификации; i-я группа представляет собой случайную выборку объема n_j наблюдений из распределения ( ² – неизвестно), . Значение i-го наблюдения, относящегося к i-й группе, можно представить в виде

где – ошибки наблюдений – независимые в совокупности нормально распределенные случайные величины или в эквивалентной форме:

(6.1)

где –

i-ый главный эффект i-го уровня признака классификации.

Выражение (6.1) носит название модели однофакторного дисперсионного анализа с фиксированными эффектами.

Типичная форма представления данных для дисперсионного анализа с классификацией по одному признаку показана в табл. 6.1.

Таблица 6.1.

Представление данных для однофакторного дисперсионного анализа

Классификация (столбцы) Номер наблюдения (строки)	1	2	. . .	k
1	y11	y12	. . .	y1k
2	y21	y22	. . .	y2k
. . .	. . .	. . .	. . .	. . .
n	yn1	yn2	. . .	ynk
Среднее по столбцу			. . .
Общее среднее

В табл.6.1 во всех столбцах имеется одно и то же число наблюдений. Однако такое встречается не всегда, поэтому мы будем вести рассмотрение в более общем виде, допуская неравное число наблюдений.

По таблице вычислим:

среднее значение группы (выборки):

где индекс j показывает, что суммирование ведется по «всем строкам j-го столбца», n_j – число наблюдений в j-ом столбце;

общее среднее:

,

где индекс (^{. .}) указывает, что суммирование ведется по всем строкам и столбцам. Если число наблюдений во всех столбцах одинаково, то , где n – число наблюдений в каждом столбце, а k – число столбцов.

§ 6.2. Проверка гипотез

Проверка гипотезы однородности наблюдений:

или в эквивалентной форме:

осуществляется путем сравнения двух выборочных дисперсий: внутригрупповой и межгрупповой , которые вычисляются по формулам:

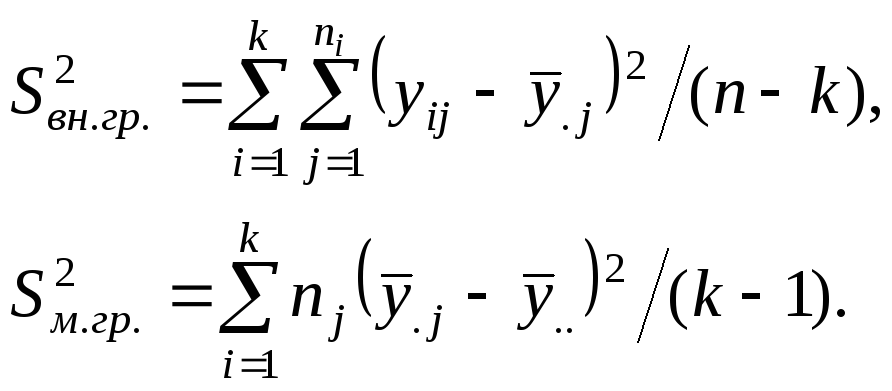
Так как и независимы и имеют распределения ² с (k – 1) и (N – k) степенями свободы соответственно, то для проверки гипотезы Н₀ используется статистика , имеющая при верной Н₀ F-распределение Фишера с (k – 1) и (N – k) степенями свободы. Гипотеза Н₀ отвергается с выбранным уровнем значимости , если вычисленное значение статистики Т_набл. превосходит табличное значение .

Если все группы имеют равные математические ожидания, т.е. Н₀ верна, то и являются несмещенными оценками дисперсии ². Если гипотеза Н₀ не верна, то по-прежнему будет несмещенной оценкой для ².

Межгрупповую дисперсию называют «ошибкой выборки», а внутригрупповую «ошибкой опыта». Результаты однофакторного дисперсионного анализа принято сводить в следующую таблицу.

Таблица 6.2.

Источник вариации	Сумма квадратов	Степени свободы	Средний квадрат	Отношение F
Различия между группами		k – 1
Различия внутри групп		N – k
Полная сумма квадратов		N – 1

Отвергая в однофакторном дисперсионном анализе гипотезу Н₀, мы делаем заключение о существенности различий между . Однако проверка с помощью F-критерия не позволяет сделать вывод, какие именно средние явились причиной неоднородности. Для решения этой задачи можно использовать процедуры множественного сравнения: S – метод Шефере, Т – метод Тьюки и множественный t-метод.

Рассмотрим линейную комбинацию средних (так называемый контраст), коэффициенты которой удовлетворяют условию .

Во всех трех перечисленных методах для проверки гипотезы

против

нужно построить доверительный интервал с надежностью для ,

,

где S – некоторая величина, зависящая от .

Гипотеза Н₀ отвергается с уровнем значимости , если доверительный интервал не содержит точку нуль. При этом

для S-метода, где

.

Пример. В таблице 6.3. приведены пятилетние нормы прибыли на обыкновенную акцию для ряда фирм в трех отраслях промышленности.

Таблица 6.3.

Сталелитейная	Электроника	Энергетика
14,6	33,6	18,6
12,0	25,1	16,3
10,5	20,6	14,4
9,9	19,6	13,3
9,3	16,7	12,7
8,7	16,0	12,0
8,7	14,1	10,9
7,7	13,1	10,2
6,6	11,6	9,5
6,2	10,3	–
5,7	8,8	–
1,1	–	–
Среднее 8,3767	17,2273	13,1000
Общее среднее		12,7438

Мы хотим на уровне значимости  = 0,05 проверить гипотезу о том, равны ли между собой все средние нормы прибыли для отдельных отраслей, т.е.

против альтернативы

Н₁: не все средние по столбцам равны.

Для проверки гипотезы заполним таблицу.

Источник вариации	Сумма квадратов	Степени свободы	Средний квадрат	Отношение F
Различия между группами		2	452,2/2=226,1	Тнабл.=9,15
Различия внутри групп		29	717,2/29=24,7
Полная сумма квадратов		31

В таблице F-распределения при  = 0,05 с 2 и 29 степенями свободы находим, что критическое значение . Поэтому гипотеза Н₀ отвергается, так как .

Выясним, какие средние значения привели к отклонению гипотезы.

Выборочные средние по столбцам равны:

(данные из табл. 6.3) с

и .

Возможны три простых линейных контраста, а именно: мы можем проверить, отвергнута ли нулевая гипотеза из-за того, что , или , или . Для проверки гипотезы

против двусторонней альтернативы .

Примем .

Аналогично, для проверки гипотезы

против двусторонней альтернативы примем .

Наконец, для проверки гипотезы

против двусторонней альтернативы примем .

Выбрав  = 0,05, находим F (2,29; 0,95) = 3,32 и для первого контраста

Таким образом, .

Так как этот интервал не покрывает нуль, то мы делаем вывод, что и являются существенно различными.

Продолжая далее аналогичным образом, мы найдем другие контрасты и определим, что

Так как эти два интервала содержат нуль, то мы делаем вывод, что на уровне значимости  = 0,05 эти два средних значения не отличаются существенно один от другого. Отсюда мы заключаем, что к отклонению совместной нулевой гипотезы привело различие между средними значениями для первых двух столбцов, т.е. для фирм сталелитейной и электронной промышленности. Нормы прибыли для фирм сталелитейной промышленности и энергетики, а также электроники и энергетики различаются несущественно.

Примером применения дисперсионного анализа в бизнесе может быть сравнение инвестиционных компаний. Многие из этих компаний утверждают, что у них высокий доход. Заказчик хочет установить, обоснованы ли эти утверждения. Для этого он выбирает k компаний, просматривает для них выборки объемов n квартальных доходов и сравнивает их.

В промышленном производстве примером использования дисперсионного анализа может быть задача о сравнении шумового уровня воздушных кондиционеров. Компания закупает часть кондиционеров у k = 5 различных предприятий. Инженеры знают, что шумовой эффект наблюдается именно у этой части кондиционеров. Исследуют и сравнивают n кондиционеров для каждой из пяти различных фирм.

В сельском хозяйстве также широко применяют дисперсионный анализ. Ученых может интересовать продуктивность различных пород скота или плантаций с различными характеристиками. Возьмем несколько видов рогатого скота. Если они содержатся в одинаковых условиях и получают одинаковый корм, то можно сравнивать их по надою молока, по его жирности и т.п.