
- •1. Пропорции. Золотое сечение.
- •2. Пропорции фигуры человека
- •3. Пропорции головы
- •4. Пропорции фигуры и головы ребенка
- •5.Оценка типа телосложения
- •Классификации конституциональных типов человека
- •Золотое сечение в строении тела человека
- •Рука человека
- •Золотая пропорция в строении легких человека
- •Строение золотого ортогонального четырехугольника и спирали.
- •Строение морских раковин
- •Золотое сечение в ухе человека
- •Рога и бивни животных, развивающиеся в форме спирали.
- •Золотое сечение в строении микромиров
- •Золотые пропорции в строении молекулы днк
- •Золотое сечение в строении снежинок
- •Золотое сечение в физике
- •Конституции и спорт
- •Конституция и раса
- •Связь конституциональных и психологических особенностей
1. Пропорции. Золотое сечение.
Знание пропорций, т.е. соотношений размеров частей человеческой фигуры, необходимо для правильного изображения человека и неудивительно, что этим всегда занимались художники и анатомы. Под пропорцией понимается соотношение частей целого между собой и этим целым. В математике пропорцией называют равенство двух отношений а : в = с : д
В эпоху Ренессанса среднепропорциональное отношение называли Божественной пропорцией. Леонардо да Винчи дает ей название «золотое сечение».
П
Рис.1.1.
Доска-панель из склепа Хеси-Ра.
Древнее царство.18 век до н.э.
ХХеси-О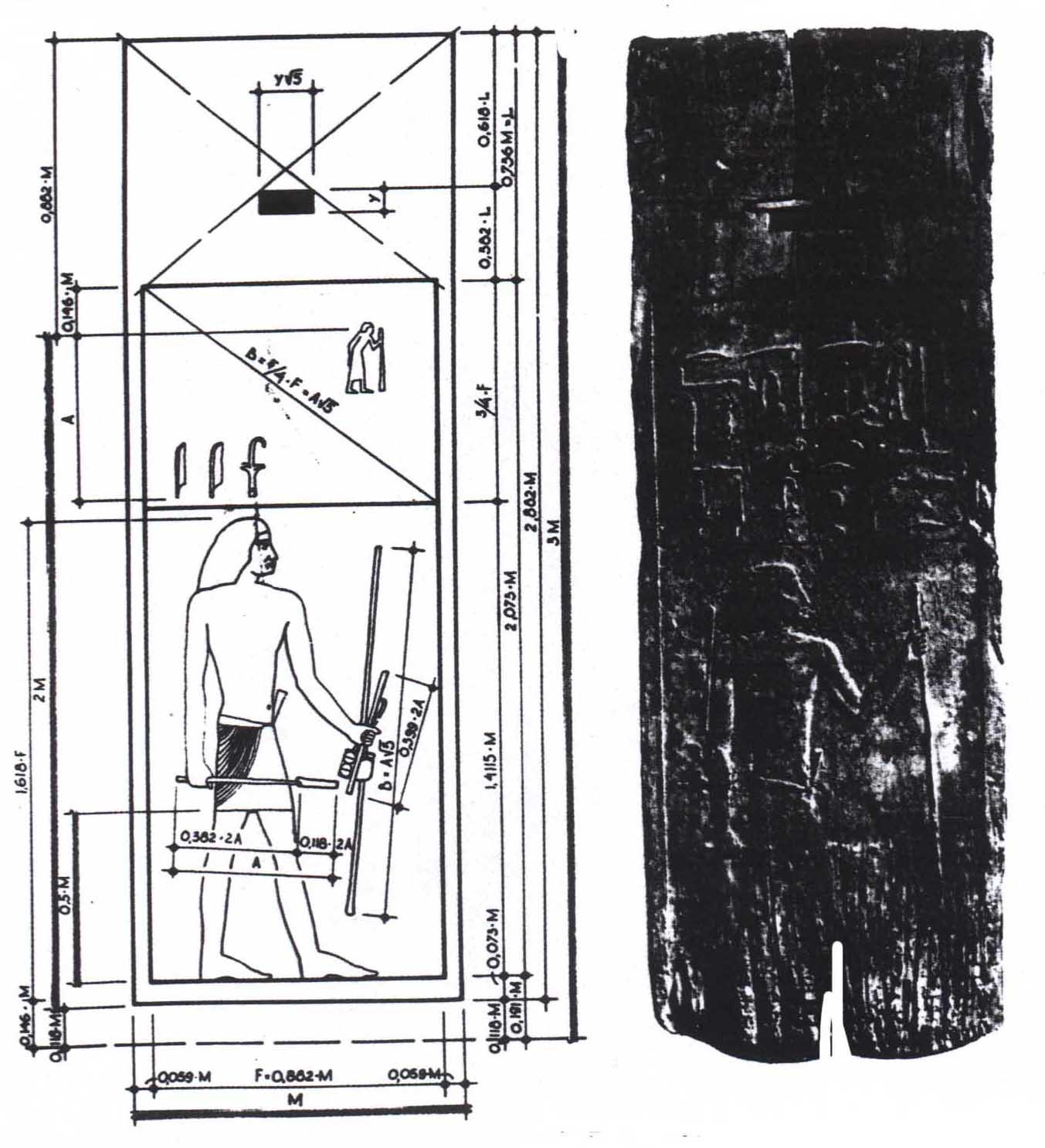 ринято
считать, что понятие о золотом сечении
ввел в научный обиход Пифагор. Есть
предположение, что Пифагор заимствовал
знания у египтян и вавилонян. И
действительно, пропорции пирамиды
Хеопса, храмов, барельефов, предметов
быта и украшений из гробницы Тутанхамона
свидетельствуют, что египетские мастера
пользовались соотношениями золотого
деления при их создании. Французский
архитектор Ле Корбюзье нашел, что в
рельефе из храма фараона Сети 1 в Абидосе
и в рельефе Рамзеса, пропорции фигур
соответствуют величинам золотого
сечения. Зодчий Хесира, изображенный
на рельефе деревянной доски из гробницы
его имени(рис.1.1.), держит в руках
измерительные инструменты, в которых
зафиксированы пропорции золотого
сечения. О золотом делении знали Платон,
Евклид, Гипсикл, Папп и др.
ринято
считать, что понятие о золотом сечении
ввел в научный обиход Пифагор. Есть
предположение, что Пифагор заимствовал
знания у египтян и вавилонян. И
действительно, пропорции пирамиды
Хеопса, храмов, барельефов, предметов
быта и украшений из гробницы Тутанхамона
свидетельствуют, что египетские мастера
пользовались соотношениями золотого
деления при их создании. Французский
архитектор Ле Корбюзье нашел, что в
рельефе из храма фараона Сети 1 в Абидосе
и в рельефе Рамзеса, пропорции фигур
соответствуют величинам золотого
сечения. Зодчий Хесира, изображенный
на рельефе деревянной доски из гробницы
его имени(рис.1.1.), держит в руках
измерительные инструменты, в которых
зафиксированы пропорции золотого
сечения. О золотом делении знали Платон,
Евклид, Гипсикл, Папп и др.
С открытием в 1202 году ряда Фибоначчи было обнаружено основное свойство золотого сечения – единство аддитивности и мультикативности. В математике понятие «аддитивность» означает, что в числовом ряду Ф1,Ф2, Ф3,Ф3,Ф4, Фn-1,Фn, каждый последующий член равен сумме двух предыдущих. Причем за начало такого ряда можно принять любые два числа, например 0 и 1, 1и 3 и т.д. Мультикативность означает, что в числовом ряду Ф1,Ф2, Ф3,Ф3,Ф4, Фn-1,Фn все члены ряда связаны в геометрическую прогрессию Ф1:Ф2 = Ф2:Ф3 = Ф3:Ф4… Фn-1:Фn =const.
Число золотого сечения, соединяющее свойства аддитивности и мультикативности, находится как общий корень двух уравнений:
а+в=с (аддитивность)
а : в = в : с (мультикативность).
Числа, образующие последовательность 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ... называются "числами Фибоначчи", а сама последовательность - последовательностью Фибоначчи. В числах Фибоначчи существует одна очень интересная особенность. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина, колеблющаяся около иррационального значения 1.61803398875... и через раз то пpевосходящая, то не достигающая его. (Прим. иррациональное число, т.е. число, десятичное представление которого бесконечно и не периодично).
Более того, после 13-ого числа в последовательности этот результат деления становится постоянным до бесконечности ряд. Именно это постоянное число деления в средние века было названо Божественной пропорцией, а ныне в наши дни именуется как золотое сечение, золотое сpеднее или золотая пропорция. В алгебpе это число обозначается гpеческой буквой фи (Ф)
Итак, Золотая пропорция = 1 : 1,618
В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи.
В 1496 году по приглашению герцога Моро в Милан приезжает математик Лука Пачоли. В то же время при дворе Моро работал и Леонардо да Винчи. В 1509 году в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства: бог сын, бог отец и бог святой дух.
Леонардо да Винчи
также много внимания уделял изучению
золотого деления. Он производил сечения
стереометрического тела, образованного
правильными пятиугольниками, и каждый
раз получал прямоугольники с отношениями
сторон в золотом делении. Поэтому он
дал этому делению название золотое
сечение. Золотое сечение - это такое
пропорциональное деление отрезка на
неравные части, при котором весь отрезок
так относится к большей части, как сама
большая часть относится к меньшей; или
другими словами, меньший отрезок так
относится к большему, как больший ко
всему.
В математике
пропорцией называют равенство двух
отношений: a:b=c:d.
Отрезок прямой АВ
можно разделить точкой C на две части
следующими способами:
на две равные
части АВ : АC = АВ : ВC;
на две неравные
части в любом отношении (такие части
пропорции не образуют);
таким образом,
когда АВ : АC = АC : ВC.
Последнее и есть
золотое деление или деление отрезка в
крайнем и среднем отношении.
 Золотое
сечение
- это такое пропорциональное деление
отрезка на неравные части, при котором
весь отрезок так относится к большей
части, как сама большая часть относится
к меньшей; или другими словами, меньший
отрезок так относится к большему, как
больший ко всему
a
: b = b : c или с : b = b : а.
Золотое
сечение
- это такое пропорциональное деление
отрезка на неравные части, при котором
весь отрезок так относится к большей
части, как сама большая часть относится
к меньшей; или другими словами, меньший
отрезок так относится к большему, как
больший ко всему
a
: b = b : c или с : b = b : а.
П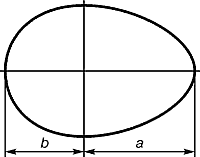

 остроим
отрезки в пропорциях золотого сечения.
В прямоугольнике с соотношением сторон
1:2 проводится диагональ, на которую
поворотом накладывается меньшая сторона.
Остаток диагонали поворачивается вокруг
вершины прямоугольника до совмещения
с положением верхнего основания. Таким
образом, верхнее основание поделилось
на два неравных отрезка в пропорции
золотого сечения.
остроим
отрезки в пропорциях золотого сечения.
В прямоугольнике с соотношением сторон
1:2 проводится диагональ, на которую
поворотом накладывается меньшая сторона.
Остаток диагонали поворачивается вокруг
вершины прямоугольника до совмещения
с положением верхнего основания. Таким
образом, верхнее основание поделилось
на два неравных отрезка в пропорции
золотого сечения.
З
Рис.1.2.
Распространение золотого сечения.
ХХеси-О
Известно, что скульптура Поликлета «Дорифор» вплоть до мельчайших деталей построена в пропорции золотого сечения (рис.1.3.)
В 20 веке Ле Корбюзье
для применения в плоскостных и объемных
композициях, создал «модулер» (рис.1.4.)
« Модулер – мерило, основанное на
сочетании математики и человеческого
масштаба; оно состоит из двух рядов
числовых величин – красного и синего
ряда. Можно ли ограничится одной числовой
таблицей? Нет. И мне вновь хочется
пояснить весь комплекс идей, положенных
в основу изобретения. Метр – это условная
в Рис.1.3.
Скульптура Поликлета «Дорифор»
ХХеси-О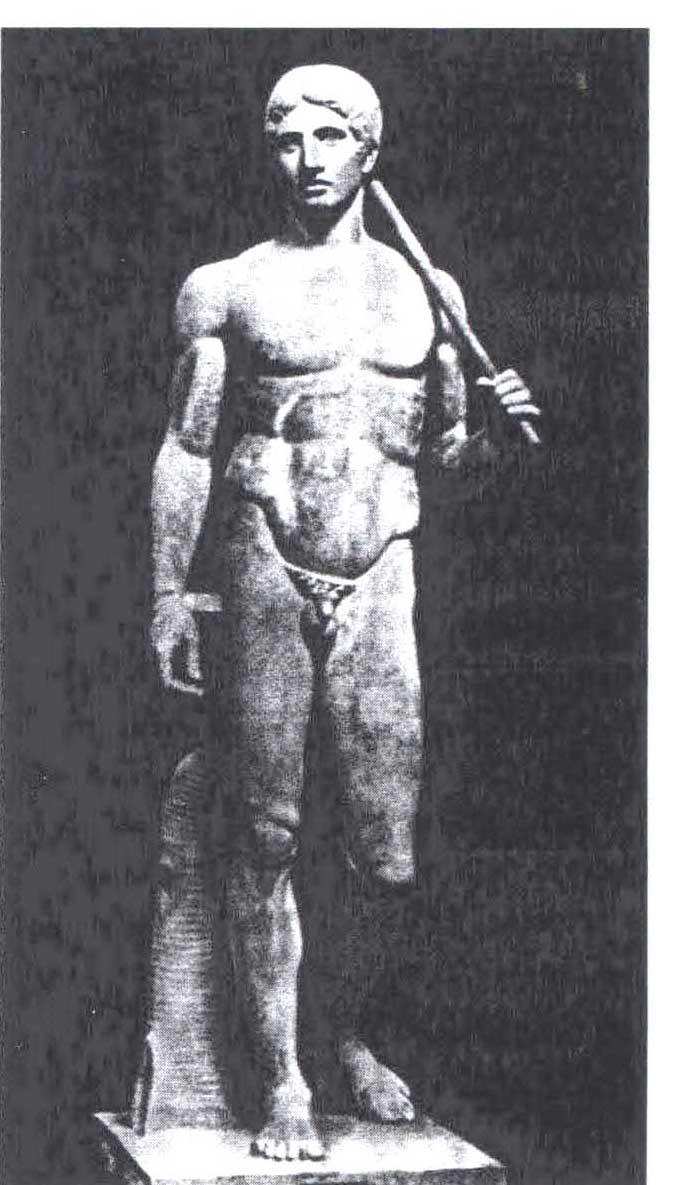 еличина…Сущность
изобретения была выражена с редкой
простотой: «модулер» - это средство
измерения, основой которого являются
рост человека и математика. Человек с
поднятой рукой дает нам точки, определяющие
занятое пространство - нога, солнечное
сплетение, голова, кончик пальцев
поднятой руки – три интервала,
обуславливающие серию золотого сечения,
называемую радом Фибоначчи. С другой
стороны, математика предлагает некоторое
и
еличина…Сущность
изобретения была выражена с редкой
простотой: «модулер» - это средство
измерения, основой которого являются
рост человека и математика. Человек с
поднятой рукой дает нам точки, определяющие
занятое пространство - нога, солнечное
сплетение, голова, кончик пальцев
поднятой руки – три интервала,
обуславливающие серию золотого сечения,
называемую радом Фибоначчи. С другой
стороны, математика предлагает некоторое
и
Вот вкратце основные позиции модулера:
 «1. Наша решетка
дате три размера:113, 70, 43 ( в см), которые
согласуются с Ф ( золотое сечение) и
рядом Фибоначчи:43+70=113 или 113-70=43. В сумме
они дают: 113+70=183, 113+70+43=226
«1. Наша решетка
дате три размера:113, 70, 43 ( в см), которые
согласуются с Ф ( золотое сечение) и
рядом Фибоначчи:43+70=113 или 113-70=43. В сумме
они дают: 113+70=183, 113+70+43=226
2. Эти три размера – 113, 183, 226 - определяют величину пространства, занимаемого человеком шести футов.
3. Размер 113 определяет золотое сечение 70, показывая начало первой, красной серии 4-6-10-16-27-43-70-113-183-226 и т.д. До сих пор, стоящий человек служил определению трех, а не четырех решающих значений модулера, а именно: 113 – солнечное сплетение, 182 –вершина головы, 226 – конец пальцев поднятой руки. Второе отношение Ф, 140-86, вводит четвертую существенную точку фигуры человека – точку опоры опущенной руки: 86 см. Таким образом, если человек, у которого левая рука понята, а правая непринужденно опущена, то она даст отметку 86. В результате мы получаем четыре точки, определяющие с помощью фигуры человека занимаемое им пространство. Размер 226 (2х113 –удвоение) определяет золотое сечение 140-86, показывая начало второй, голубой, серии: 13-20,3 -33-53-86-140-226-366-592 и т.д.
4. Из этих значений и размеров отметим те, которые определенно связаны с ростом человека…»
Практические задания
-
Постройте посредством циркуля и линейки два отрезка в пропорциях золотого сечения. Затем меньший из них опять поделите в пропорции Ф (золотого сечения) на два отрезка и т.д.
-
Возьмите рисунок скульптуры Поликлета. Попробуйте составить схему пропорционирования.
-
П
 ользуясь
рис.1.4. «Золотые пропорции в частях тела
человека и фигуры человека» докажите
свойства золотого сечения.
ользуясь
рис.1.4. «Золотые пропорции в частях тела
человека и фигуры человека» докажите
свойства золотого сечения.
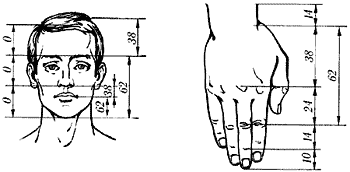
Рис.1.4.Золотые
пропорции в частях тела человека и
фигуры человека
ХХеси-О
Вопросы для самоконтроля и взаимного контроля
-
Дайте определение золотого сечения.
-
Кто ввел понятие о золотом делении?
-
Какой вклад внес Леонардо да Винчи в разработку вопроса о золотом сечении?
-
По мнению Луки Пачоли золотая пропорция содержит «божественную суть». В чем она заключается?
-
В чем состоит основное свойство золотого сечения?
-
Каково назначение «модулера» Корбюзье?
-
Приведите примеры как и где проявляет себя золотое сечение? В природе, архитектуре, промышленности? (по возможности подобрать рисунки и проиллюстрировать)
