
- •Практическое занятие n 8 по дисциплине математика
- •Практическое занятие n 8 Тема “Определители третьего порядка”
- •Краткая теория.
- •1. Определение матрицы .
- •2. Свойства определителя третьего порядка .
- •3. Решение систем уравнений с тремя неизвестными с помощью определителя третьего порядка .
- •4. Решение однородных систем уравнений с тремя неизвестными с помощью определителя третьего порядка .
- •Задания
- •Карта полученных результатов
- •6. Ответить на контрольные вопросы.
МИНИСТЕРСТВО
ОБРАЗОВАНИЯ РФ
ГОУ
МИАССКИЙ ЭЛЕКТРОМЕХАНИЧЕСКИЙ ТЕХНИКУМ
РАССМОТРЕНО
на
заседании цикловой комиссии
спец.
“Естественно-научных дисц.”
Протокол
N____
от ________2004г.
Председатель
цикловой комиссии
____________/С.В.Скоробогатова
/
УТВЕРЖДАЮ
Зам.директора
по УПР
_______/И.В.Карпов/
“____”________2004г.
“Определители
3 порядка”
Курс
II
Специальности
(технические -1201,1209)
Разработал:________/Н.И.Буяндуков/
2004
г.
Цель:
. Научится алгоритму нахождения
определителя третьего порядка.
Оборудование:
Карточки-задания, микрокалькулятор,
линейка, карандаш.
Порядок выполнения
практического занятия.
1.
Ознакомиться с кратким теоретическим
содержанием для выполнения практического
занятия.
2.
Выполнить предложенные задания.
3.
Результаты, полученные при выполнении
заданий, занести в таблицу.
4.
Ответить на контрольные вопросы.
Матрицей
размеров m х n называется совокупность
m·n чисел расположенных в виде прямоугольной
таблицы из m-строк и n-столбцов.
Примеры матриц:
1.
2.
3.
4.
5.
6.
Матрица размеров
n х n называется квадратной
матрицей,
а число n называется порядком
матрицы.
Примеры квадратных
матриц:
1.
2.
Рассмотрим
квадратную (квадратичную) матрицу 3-го
порядка, состоящую из 9 чисел.
Для вычисления
будем использовать данный вид матрицы
Числа
Определителем
(детерминантом) третьего порядка,
соответствующим данной матрице
называется число, получаемое следующим
образом
и обозначается
Таким образом
согласно определения
Формулу (4) называют
разложением определителя третьего
порядка по элементам первой строки.
Из определения
следует, что вычисление определителя
третьего порядка сводится к вычислению
определителя второго порядка.
Пример 1:
Вычислить определитель 3-го порядка:
Определитель 3-го
порядка можно находить не только через
разложение 1 строки, но и через другие
элементы строки или столбца.
Для этого
используется следующая таблица:
Тогда выполняются
следующие тождества
Подобные разложения
используются для удобства вычислений.
Пример 2: Вычислить
определитель 3-го порядка:
Разложим по
элементам 2 строки:
Определители
третьего порядка обладают следующими
свойствами:
1. Величина
определителя не изменится, если его
строки поменять местами с соответствующими
столбцами.
2. При перестановке
двух строк (или столбцов) определитель
изменит знак на противоположный,
сохраняя абсолютную величину.
3. Определитель с
двумя одинаковыми строками (или
столбцами) равен нулю.
4. Общий множитель
всех элементов строки (или столбца)
можно выносить за знак определителя.
5. Если элементы
какой-либо строки (или столбца) равны
нулю, то определитель равен нулю.
6. Если к элементам
какой-либо строки (столбца) определителя
прибавить соответственные элементы
другой строки (столбца),умноженные на
одно и то же число, то величина определителя
не изменится.
Пример 3
: Вычислить определитель 3-го порядка
Решение:
а). Вынесем за знак
определителя общие множители каждой
строки:
б). третью строку
прибавим к первой и второй строке
соответственно:
в). вычислим
окончательно, разложив последнее
выражение по элементам первой строки:
Ответ: 10800.
Определитель
третьего порядка позволяет решать
систему трех уравнений с тремя
переменными.
Пусть дана система
трех уравнений с тремя неизвестными:
Обозначим
определители третьего порядка через
:
тогда корни системы
трех уравнений с тремя неизвестными
определяются следующим образом:
полученные формулы
(16 - 18) называют формулами
Крамера.
Пример 4.
Решить систему уравнений, используя
формулы Крамера:
Решение:
Найдем по формуле
(12) определитель D третьего порядка:
Следовательно
система уравнений имеет единственное
решение.
Далее по формулам
(13 - 15) найдем
Затем по формулам
Крамера (16 - 18) находим корни исходной
системы:
Ответ: ( 2; 3; 1)
Если определитель
D = 0, то исходная система является:
- неопределенной
(
- несовместной
(
Пример 5.
Решить систему уравнений, используя
формулы Крамера:
Решение:
Найдем по формуле
(12) определитель D третьего порядка:
Итак
Действительно
умножая 1-е уравнение на 3 и вычитая 3-е
уравнение придем к невозможному:
получим (3х - 3х) +
(-3у -(-3у)) + (6z
- 6z) = 6 - 3 , откуда следует 0 = 3 , не имеет
смысла.
Ответ: Нет корней.
Пример 6.
Решить систему уравнений, используя
формулы Крамера:
Решение:
Найдем по формуле
(12) определитель D третьего порядка:
Итак
Задавая произвольное
значение х мы будем получать соответственное
значение у и z .
при х = 1
откуда
Итак
при х = 0
Итак
Ответ: Бесчисленное
множество решений.
Пример 7.
Решить систему уравнений, используя
формулы Крамера:
Решение:
Найдем по формуле
(12) определитель D третьего порядка:
т.к.
Ответ: Нет корней.
Определитель
третьего порядка позволяет решать
однородные системы трех уравнений с
тремя переменными.
Система вида
называется
однородной
системой
трех уравнений с тремя переменными.
Если
х = у = z = 0 или ( 0;
0; 0; ).
Если
- к двум независимым
уравнениям (3-е уравнение является их
следствием) , либо
- к одному уравнению
(два других уравнения является его
следствиями).
Первый случай
имеет место тогда, когда среди миноров
определителя однородной системы есть
хотя бы один отличный от нуля.
Второй случай
имеет место тогда, когда все миноры
определителя однородной системы равны
нулю.
Рассмотрим систему
2-х линейных уравнений с 3-мя неизвестными:
1. Если
2. Если условие
где
Пример 8.
Решить систему 2 линейных однородных
уравнений:
Решение:
Используя формулы
( 21 - 23 ) находим:
где t - любое число.
Ответ: х = -22t ; у =
14t ; z = 2t , где t - любое число.
Ответ можно
записать и таким образом ( -22t; 14t; 2t ), где
t - любое число.
Пример 9.
Решить систему линейных однородных
уравнений:
Решение:
Найдем по формуле
(12) определитель D третьего порядка:
Т.к.
Ответ: ( 0; 0; 0; ).
Пример 10.
Решить систему линейных однородных
уравнений:
Решение:
Найдем по формуле
(12) определитель D третьего порядка:
Т.к.
Решаем систему
двух линейных уравнений с тремя
неизвестными (3 - уравнение является их
следствием)
Используя формулы
( 21 - 23 ) находим:
где t - любое число.
Ответ: ( 20t; ─28t; 4t
), где t - любое число.
Задание 1.
Вычислить определитель третьего
порядка. №
варианта
Исходные данные
№ варианта
Исходные данные
Вариант 1
Вариант 9
Вариант 2
Вариант 10
Вариант 3
Вариант 11
Вариант 4
Вариант 12
Вариант 5
Вариант 13
Вариант 6
Вариант 14
Вариант 7
Вариант 15
Вариант 8
Вариант 16
Задание 2.
Вычислить определитель третьего
порядка, используя его свойства
№ варианта
Исходные данные
№ варианта
Исходные данные
Вариант 1
Вариант 9
Вариант 2
Вариант 10
Вариант 3
Вариант 11
Вариант 4
Вариант 12
Вариант 5
Вариант 13
Вариант 6
Вариант 14
Вариант 7
Вариант 15
Вариант 8
Вариант 16
Задание 3. Решить
систему уравнений, используя формулы
Крамера:
№ варианта
Исходные данные
№ варианта
Исходные данные
Вариант 1
Вариант 9
Вариант 2
Вариант 10
Вариант 3
Вариант 11
Вариант 4
Вариант 12
Вариант 5
Вариант 13
Вариант 6
Вариант 14
Вариант 7
Вариант 15
Вариант 8
Вариант 16
Задание 4. Решить
систему уравнений, используя формулы
Крамера:
№ варианта
Исходные данные
№ варианта
Исходные данные
Вариант 1
Вариант 9
Вариант 2
Вариант 10
Вариант 3
Вариант 11
Вариант 4
Вариант 12
Вариант 5
Вариант 13
Вариант 6
Вариант 14
Вариант 7
Вариант 15
Вариант 8
Вариант 16
Задание 5. Решить
систему однородных уравнений:
№ варианта
Исходные данные
№ варианта
Исходные данные
Вариант 1
Вариант 9
Вариант 2
Вариант 10
Вариант 3
Вариант 11
Вариант 4
Вариант 12
Вариант 5
Вариант 13
Вариант 6
Вариант 14
Вариант 7
Вариант 15
Вариант 8
Вариант 16
№ задания
Результаты
выполненных заданий (ответы) Задание
1
Задание 2
Задание 3
Задание 4
Задание 5
Контрольные
вопросы:
1. Что называется
матрицей ?
2. Привести примеры
матриц.
3. Что называется
квадратичной матрицей ?
4. Что называется
порядком матрицы ?
5. Что называется
порядком элементами матрицы ?
6. Что называется
определителем третьего порядка ?
7. Записать формулу
разложения определителя третьего
порядка по элементам первой строки .
8. Что называется
минором данного элемента определителя
третьего порядка ?
9. Как обозначается
минор данного элемента определителя
третьего порядка ?
10. Записать формулу
разложения определителя третьего
порядка по элементам второй строки .
11. Записать формулу
разложения определителя третьего
порядка по элементам третьей строки .
12. Записать формулу
разложения определителя третьего
порядка по элементам первого столбца
.
13. Записать формулу
разложения определителя третьего
порядка по элементам второго столбца
.
14. Записать формулу
разложения определителя третьего
порядка по элементам третьего столбца
.
15. Свойства
определителя третьего порядка .
16. Прочитать
свойство определителя третьего порядка
, выраженного формулой:
17. Прочитать
свойство определителя третьего порядка
, выраженного формулой:
18. Прочитать
свойство определителя третьего порядка
, выраженного формулой:
19. Прочитать
свойство определителя третьего порядка
, выраженного формулой:
20. Прочитать
свойство определителя третьего порядка
, выраженного формулой:
21. Прочитать
свойство определителя третьего порядка
, выраженного формулой:
22. Какое условие
необходимо для единственного решения
системы трех уравнений с тремя переменными
?
23. Как определяется
Dx
при решении системы трех уравнений с
тремя переменными ?
24. Как определяется
Dy
при решении системы трех уравнений с
тремя переменными ?
25. Как определяется
Dz
при решении системы трех уравнений с
тремя переменными ?
26. Как определяется
корень х при решении системы трех
уравнений с тремя переменными через
Dх
?
27. Как определяется
корень у при решении системы трех
уравнений с тремя переменными через
Dу
?
28. Как определяется
корень у при решении системы трех
уравнений с тремя переменными через
Dz
?
29. Назвать формулы
Крамера.
30. При каком условии
система трех уравнений с тремя переменными
является несовместной через детерминанты
третьего порядка ?
31. При каком условии
система трех уравнений с тремя переменными
является неопределенной через
детерминанты третьего порядка ?
32. Какая система
трех уравнений с тремя переменными
называется однородной ?
33. Какое решение
имеет однородная система трех уравнений
с тремя переменными, если D # 0 .
34. Какое решение
имеет однородная система трех уравнений
с тремя переменными, если D = 0 .
35. Когда однородная
система трех уравнений с тремя переменными
приводится к одному уравнению ?
36. Когда однородная
система трех уравнений с тремя переменными
приводится к двум независимым линейным
уравнениям с тремя неизвестными ?
37. Как определяются
корни однородной системы двух уравнений
с тремя переменными ?
Отчет о проделанной
работе.
1. Цель работы.
2. Задание.
3. Выписать формулы,
необходимые для вычислений.
4. Описание решения
заданий.
5. Оформить карту
полученных результатов (внести ответы).
24
Практическое занятие n 8 по дисциплине математика
Практическое занятие n 8 Тема “Определители третьего порядка”
Краткая теория.
1. Определение матрицы .
 (1)
(1) матрица размеров 2 х 3
матрица размеров 2 х 3![]() матрица размеров 3 х 2
матрица размеров 3 х 2![]() матрица размеров 1 х 4
матрица размеров 1 х 4![]() матрица размеров 4 х 1
матрица размеров 4 х 1![]() матрица размеров 1 х n
матрица размеров 1 х n матрица размеров m
х 1
матрица размеров m
х 1![]() матрица размеров 2 х 2 (квадратная
матрица 2-го порядка)
матрица размеров 2 х 2 (квадратная
матрица 2-го порядка) матрица размеров 3 х 3 (квадратная
матрица 3-го порядка)
матрица размеров 3 х 3 (квадратная
матрица 3-го порядка) или
или
 (2)
(2)
![]() - называются элементами
матрицы.
- называются элементами
матрицы.![]() (3)
(3)
 =
=![]() (4)
(4)

 и
т.д.
и
т.д.

2. Свойства определителя третьего порядка .
 (5)
(5) (6)
(6) или
или
 (7)
(7) (8)
(8) или
или
 (9)
(9) (10)
(10)
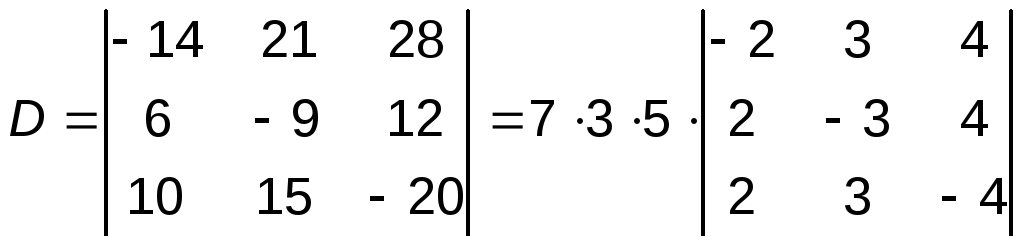 ;
; ;
;
3. Решение систем уравнений с тремя неизвестными с помощью определителя третьего порядка .
 (11)
(11) (12)
(12)  (13)
(13) (14)
(14)  (15)
(15)![]() (16),
(16), ![]() (17)
(17)
![]() (18).
(18).


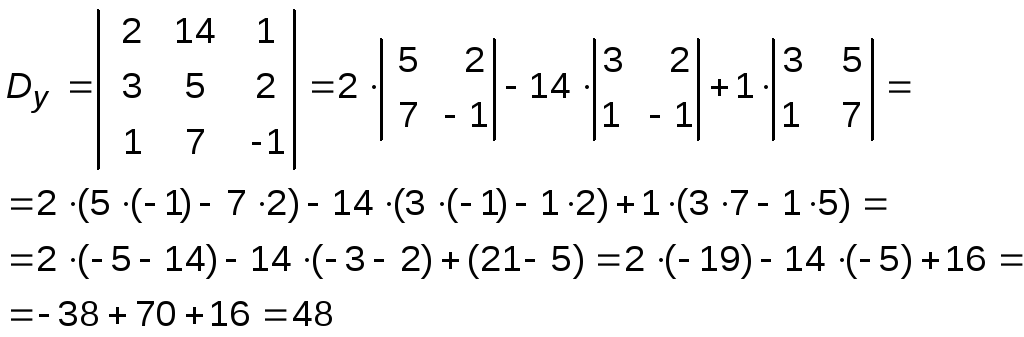

![]() ;
; ![]() ;
; ![]() .
.![]() ,
то система либо не имеет решений или
имеет бесконечное множество решений);
,
то система либо не имеет решений или
имеет бесконечное множество решений);![]() и по крайней мере один из определителей
и по крайней мере один из определителей
![]() ,
,
![]() или
или
![]() не равен нулю, то система не имеет
решений);
не равен нулю, то система не имеет
решений);

 ,
т.к элементы 1 и 3 столбца пропорциональны
друг другу.
,
т.к элементы 1 и 3 столбца пропорциональны
друг другу. ,
аналогично предыдущему свойству.
,
аналогично предыдущему свойству. ,
т.к элементы 1 и 3 столбца пропорциональны
друг другу.
,
т.к элементы 1 и 3 столбца пропорциональны
друг другу. ,
т.к элементы 1 и 2 столбца пропорциональны
друг другу.
,
т.к элементы 1 и 2 столбца пропорциональны
друг другу.![]() ,
то система не имеет решений, т.к. первое
и третье уравнения противоречивы, а
именно х - у + 2z = 2 и 3х - 3у + 6z = 3 не имеет
смысла.
,
то система не имеет решений, т.к. первое
и третье уравнения противоречивы, а
именно х - у + 2z = 2 и 3х - 3у + 6z = 3 не имеет
смысла.
 ,
,

 ,
т.к элементы 1 и 2 строки пропорциональны
друг другу.
,
т.к элементы 1 и 2 строки пропорциональны
друг другу. ,
аналогично предыдущему свойству.
,
аналогично предыдущему свойству. ,
т.к элементы 1 и 2 строки пропорциональны
друг другу.
,
т.к элементы 1 и 2 строки пропорциональны
друг другу. ,
т.к элементы 1 и 3 столбца пропорциональны
друг другу.
,
т.к элементы 1 и 3 столбца пропорциональны
друг другу.![]() ,
то система имеет бесконечное множество
решений, т.к. 2-е уравнение получается
умножением 1-го уравнения на 2., то
указанная система равносильна системе
2-х уравнений:
,
то система имеет бесконечное множество
решений, т.к. 2-е уравнение получается
умножением 1-го уравнения на 2., то
указанная система равносильна системе
2-х уравнений: ,
откуда
,
откуда

 ,
следует
,
следует
 ,
решая которое имеем
,
решая которое имеем ,
, 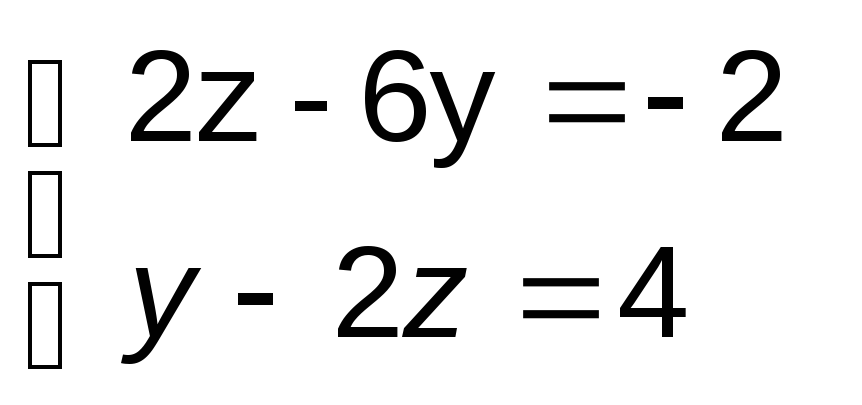 ,
, ![]() ,
,
,
,![]() .
Тогда
.
Тогда
![]() .
.![]() и
и
![]()
 ,
следует
,
следует
 ,
решая которое имеем
,
решая которое имеем ,
,  ,
, ![]() ,
,откуда
,
,откуда
![]() .
Тогда
.
Тогда
![]() .
.![]() и
и
![]()

 ,
т.к элементы 1 и 3 строки пропорциональны
друг другу.
,
т.к элементы 1 и 3 строки пропорциональны
друг другу. ,
,![]() и
и
![]() ,
то система не имеет решений.
,
то система не имеет решений.4. Решение однородных систем уравнений с тремя неизвестными с помощью определителя третьего порядка .
 (19)
(19)![]() ,
то система имеет единственное нулевое
решение
,
то система имеет единственное нулевое
решение
![]() ,
то система сводится:
,
то система сводится: (20)
(20)![]() ,
то система сводится к одному уравнению,
(например к первому), из которого одно
из неизвестных выражается через два
других, значения которых остаются
произвольными.
,
то система сводится к одному уравнению,
(например к первому), из которого одно
из неизвестных выражается через два
других, значения которых остаются
произвольными.![]() не выполняется, т.е. не всегда коэффициенты
при переменных пропорциональны, то
решение системы находятся по формулам:
не выполняется, т.е. не всегда коэффициенты
при переменных пропорциональны, то
решение системы находятся по формулам:![]() (21)
(21) (22)
(22)![]() (23),
(23),
![]() - может принимать любые значения.
- может принимать любые значения.


![]() ,
,
 .
.
![]() ,
то система имеет единственное нулевое
решение х = у = z = 0 .
,
то система имеет единственное нулевое
решение х = у = z = 0 . .
. ,
,![]() ,
то система имеет решение, отличное от
нулевого.
,
то система имеет решение, отличное от
нулевого.


![]() ,
,
Задания

















![]()
![]()

![]()
![]()

![]()


![]()
![]()

![]()
![]()















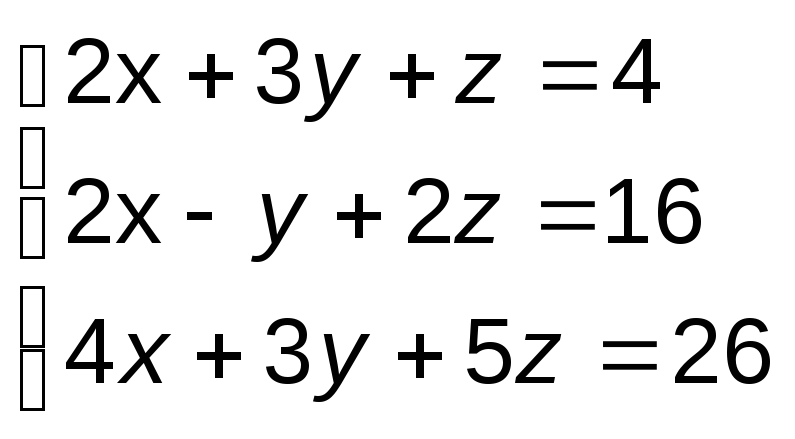

































Карта полученных результатов


 или
или


 или
или


6. Ответить на контрольные вопросы.
2
23
3
22
4
21
5
20
6
19
7
18
8
17
9
16
10
15
11
14
12
13
