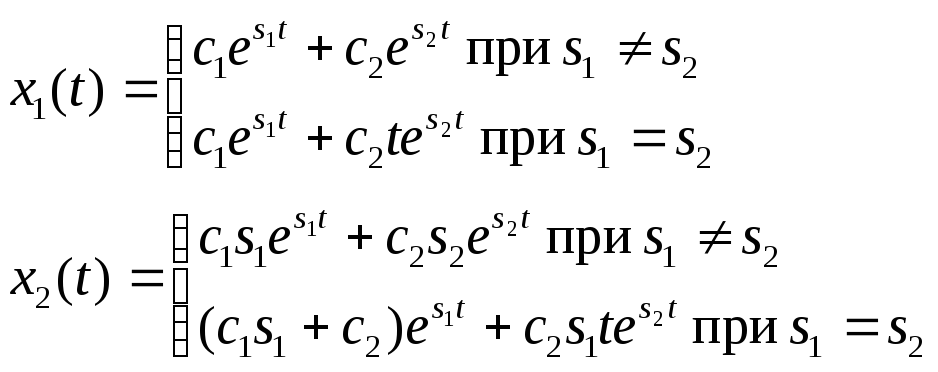1.6. Линеаризация нелинейных систем

Большинство реальных систем нелинейны, т.е. поведение системы описывается уравнениями:

Часто на практике нелинейные системы можно аппроксимировать линейной в некоторой ограниченной области.

Предположим, что для уравнения (1) известно. Заменим систему (1,2) подставив начальные условия

Предполагаем, что начальные состояния и входная переменная изменены так, что новое состояние и входная переменная имеет следующий вид.

Выход найдем в результате решения возмущенных уравнений.

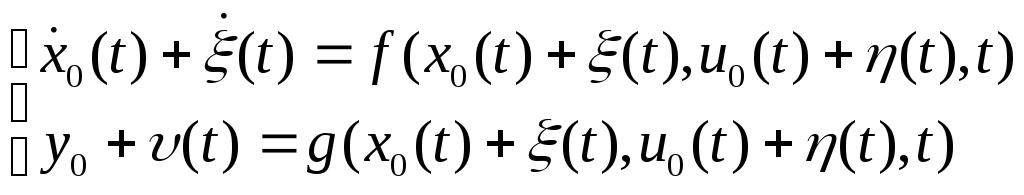
Разложим правую часть в ряд Тейлора.

(5)

(6)

-остаточный член погрешности второго порядка малости.

Вычитая исходное решение из разложений, получаем следующие линеаризованные уравнения:

.

Частные производные обозначим как коэффициенты зависящие от времени

Эти выражения можно переписать в виде

Пример 1.

Получим линеаризованные уравнения в точках равновесия.

. В точке

В точке

Пример 2.

Решение этого уравнения

Продифференцируем правую часть исходного уравнения по x , получим

.

Выполним линеаризацию уравнения для произвольного начального значения.

Получаем линеаризованную систему в виде нестационарного уравнения

Решение линеаризованной системы имеет вид:

.

1.7. Типовые возмущающие воздействия

Внешние возмущающие воздействия могут иметь различный характер:

мгновенного действия виде импульса и постоянного действия.

1. Воздействие в виде ступенчатого мгновенного изменения входных координат.

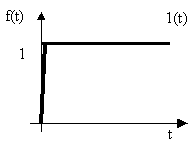
   f(t)=1(t) – единичная функция Хевисайда , при t = - 0 , f(t)=0, при t = +0 , f(t) =1.

2. Мгновенный единичный импульс первого рода определяется дельта – функцией (t).

При t=0 (t) =, при t =  (t) стремится к 0. Одним из примеров аппроксимации (t)- функции есть . По условию воздействия импульс должен быть единичным поэтому , т.е. площадь под кривой = 1

Если продифференцировать во времени , то, следовательно(t)- функция представляет собой производную во времени единичного ступенчатого воздействия.

(t)- функция при интегрировании обладает следующими фильтрующими свойствами:

.

Интегрируемое произведение произвольной функции и(t)- функции отфильтровывает из всех значений только то, которое соответствует моменту приложение мгновенного единичного импульса.

Линейное возмущение

Гармоническое возмущение

2 U. Системы второго порядка

2.1.Приведение уравнений второго порядка к системам уравнений первого порядка

Пример линейной стационарной системы.

(1)

.

Другое описание этой же системы второго порядка дается парой связанных дифференциальных уравнений первого порядка

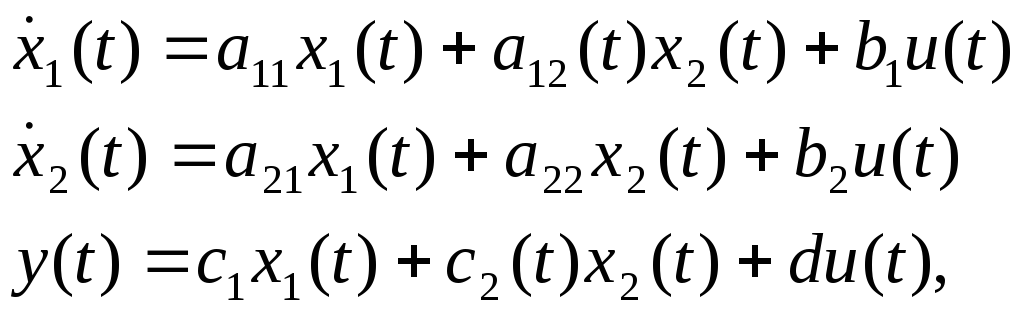(2)

где связь между коэффициентами этих уравнений определяется следующими соотношениями

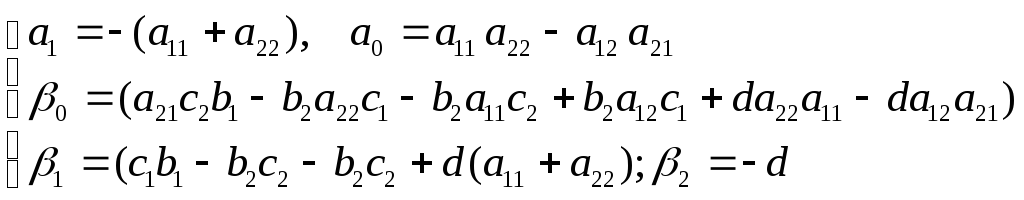
2.2. Решение уравнений второго порядка

Применяя дифференциальный оператор уравнение можно представить в более компактном виде

(3)

Решается уравнение (1) в 3 этапа:

1) находим общее решение однородного уравнения;

2) находим частное решение ;

3) полное решение есть сумма этих двух решений .

Рассматриваем однородное уравнение

(4)

будем искать решение в форме

(5)

где действительная или комплексная величина. При подстановке (5) в (4) получаем

(6)

Это выражение является решением однородного уравнения, если s удовлетворяет характеристическому уравнению

При s₁  s₂ решение однородного уравнения имеет вид

Тогда ищем решение в виде и подставляя его в исходное уравнение

(7)

Откуда следует, что .

Если выбрать

. (8)

Частное решение исходного уравнения (1) ищем методом вариации в форме

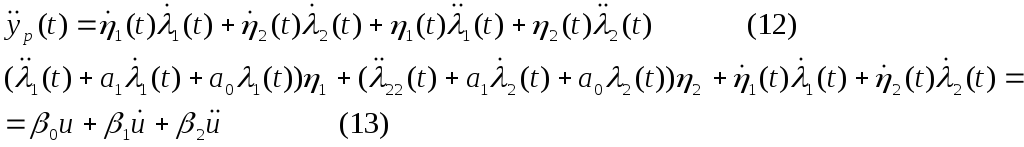
исходя из (11), (13) получаем систему

Полное решение уравнения.

Пример

Заменой переменных получим уравнение второго порядка:

3. ФАЗОВАЯ ПЛОСКОСТЬ

Двумерным пространственным состоянием или фазовой плоскостью называется плоскость, в которой две переменные состояния рассматриваются в прямоугольной системе координат

- эти переменные состояния образуют вектор .

График измененияобразует траекторию движения. Необходимо указать направление движения траектории.

Состояние равновесия называется такое состояние , в котором система остается при условии, чтоСостояние равновесия можно определить (если оно существует) из соотношений

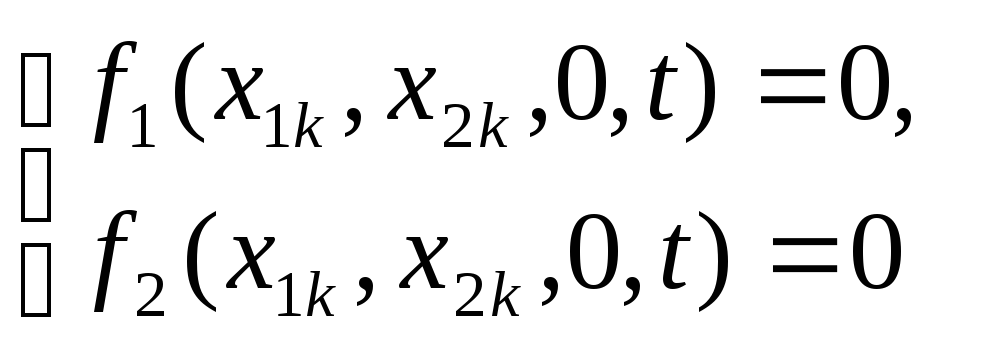
при любом t.

Состояния равновесия иногда называются критическими, основными или нулевыми точками.

Траектории системы не могут пересекаться друг с другом в пространстве, что вытекает и единственности решения дифференциального уравнения.

Ни одна траектория не проходит через состояние равновесия хотя и могут сколь угодно близко приближаться к особым точкам (при ) .

Типы точек

1 Регулярная точка есть любая точка, через которую может проходить траектория, точка равновесия не является регулярной.

2.Точка равновесия изолирована, если в ее малой окрестности содержатся только регулярные точки.

Рассмотрим систему

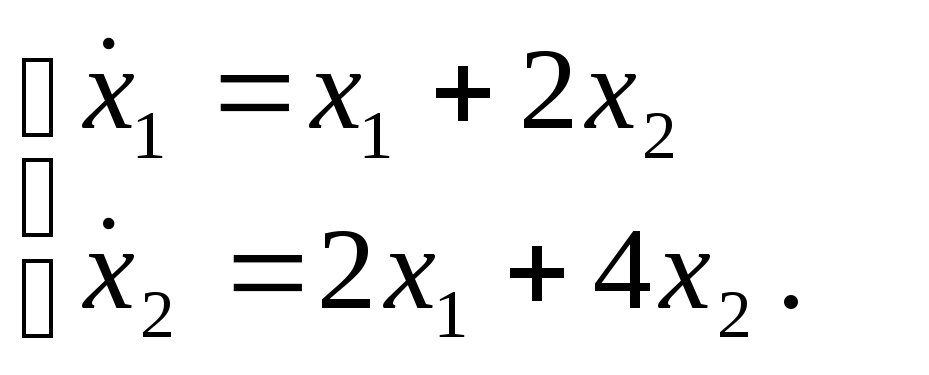
Для определения состояния равновесия решим следующую систему уравнений

.

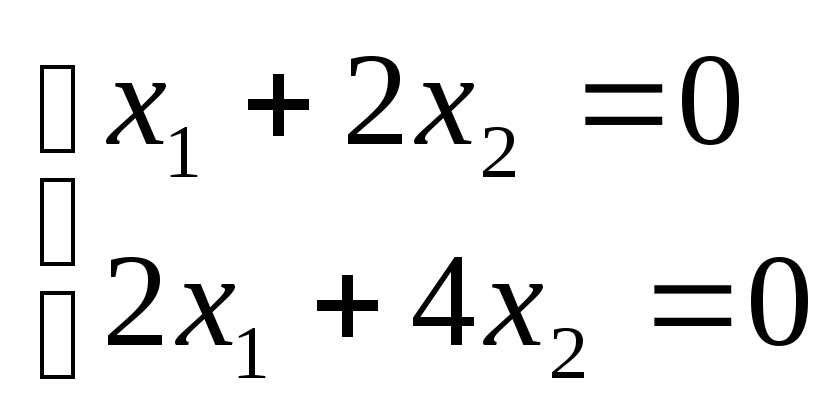Получаем зависимость между переменными состояния .

любая точка которой есть состояние равновесия. Эти точки не является изолированными.

Заметим, что для линейной стационарной системы

начальное состояние оказывается состоянием равновесия и изолированным, если детерминант матрицы коэффициентов , тогдаесть состояние равновесия.

Для нелинейной системы второго порядка состояние равновесия называется простым, если соответствующая матрица Якоби не равна 0.

В противном случае состояние не будет простым. Если точка равновесия является простой, то она изолирована. Обратное утверждение не обязательно верно ( за исключением случая линейных стационарных систем) .

Рассмотрим решение уравнения состояния для линейной системи второго порядка: .

Эту систему можно представить двумя уравнениями первого порядка,

обозначим ,

тогда

Характеристическое уравнение и решение будет следующим:

Решение уравнения записывается в виде