2.5. Решение уравнений состояния n-го порядка

Рассмотрим уравнение состояния стационарного управляемого объекта

u­- вектор входных воздействий, W - вектор возмущающих воздействий. Задача состоит в вычислении при.

Уравнению (1) соответствует однородное уравнение , решение которого равно

Введя обозначение решение можно представить в виде:

Пусть решение неоднородного уравнения (1) равно:

(2)

Дифференцируя уравнение (2) по t, получим

(3)

Сравнивая (1) и (3) , имеем

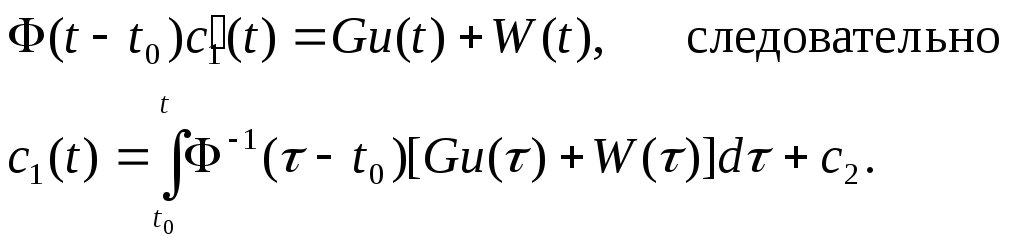
Решение уравнения

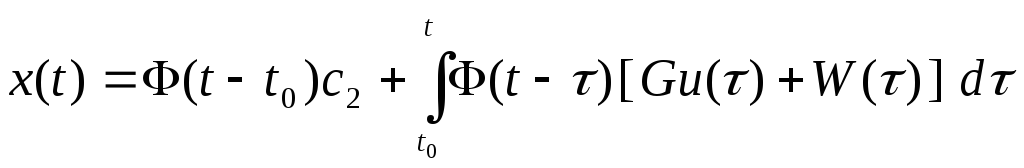(4)

В уравнении (4) учтено, что не зависит от переменной интегрирования и

Вектор вычисляется по начальным условиям.

Окончательная форма решения уравнения

Отметим, что - называется фундаментальной матрицей системы, для которой верны свойства:

3. Элементы теории матриц

3.1. Линейные векторные пространства

Множество векторов называется линейным векторным пространством, если для любых двух векторов определена операция сложения и для любого вектора определены операции умножения на число, при выполнении аксиом сложения векторов и умножения на скаляр. Простейший пример векторного пространства – множество упорядоченных пар действительных чисел. Геометрическим представлением такого линейного векторного пространства является плоскость. Это пространство называется двумерным Евклидовым пространством .

МЕТРИКА

Расстояние между двумя векторамизадают с помощью метрики, удовлетворяющей следующим аксиомам:

Пусть  и  векторы пространства .

Вычислим расстояние между векторами для каждой из приведенных выше метрик.

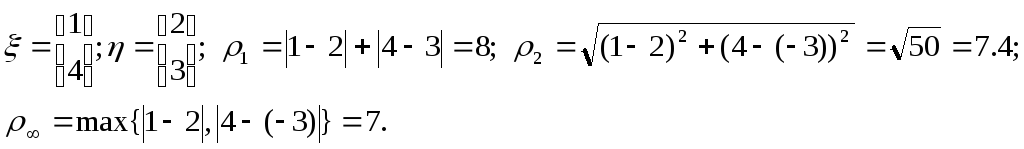
В каждой из этих метрик можно определить единичную окружность как множество всех точек расстояние которых от начала координат .

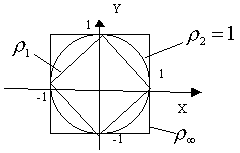
Линейное векторное пространство называетсянормированным, если каждому вектору можно поставить в соответствие неотрицательное число, называемое нормой, удовлетворяющее следующим свойствам:

1. тогда и только тогда, когда х=0,

2. ,

3. .

В нормированном пространстве можно ввести метрику по формуле .

Норму вектора можно определить через метрику как расстояние между вектором и нулевым вектором: .

Размерность. Линейное векторное пространство называется конечномерным, а числоn называется размерностью пространства, если существует n-линейно независимых векторов из и любыевекторов излинейно зависимы.

Если пространство содержит сколь угодно большого количества линейно независимых векторов, то оно называется бесконечно мерным пространством.

Базис- множество линейно независимых векторов называется базисом линейного векторного пространства, если любой векторпредставляется в виде:

- числа (определяются однозначно).

Преобразование называется оператор, отображающий пространство, то есть преобразование сопоставляет каждомуn-вектору только один m-вектор и записывается в виде .

Преобразование Т называется однозначным, если при любом

Преобразование Т называется линейным если , где.

Линейному преобразованию Т можно сопоставить матрицу А, т.е..

3.2. Собственные векторы и собственные значения

Множество называется линейным подпространством, еслии для любых. Подпространствоназывается инвариантным подпространством относительно преобразования Т, если для любогоВ действительном пространствеодномерное пространство- это прямая проходящая через начало координат. Если(где)инвариантное подпространство линейного подпространства Т, то в силу определения инвариантного подпространства дает нам результатгде- число .

Используя матричное представление преобразования получим , сократим на , получим .

Если не нулевой векторудовлетворяет этому соотношению, то ему удовлетворяет также любой вектор полученный умножениемна любое действительное или комплексное число. Следовательно, векторопределяет одномерное инвариантное подпространство преобразования Т, представленное в базисематрицы А. Уравнениепредставляет собой систему линейных однородных алгебраических уравнений. Эта система имеет однозначное решение, если только.

Значение вектора всегда является решением такой системы. С другой стороны, если, то решение будет не единственным и нетривиальное решение () в этом случае существует.

Определим характеристический полином как:гдеи.

Корни характеристического уравнения называютсясобственными значениями или характеристическими числами матрицы А.

Из основной теоремы алгебры следует, что характеристическое уравнение имеетn корней, некоторые из которых могут совпасть, а некоторые могут быть комплексными.

Каждому собственному значению из набора соответствует член из множествасобственных векторов, т.е. собственный вектор является ненулевым решением уравнения.

Если все собственные значения различны, n соответствующих собственных векторов линейно независимы и следовательно образуют базис пространства .

Пример

Рассмотрим линейное преобразование А:

. Запишем его характеристический полином

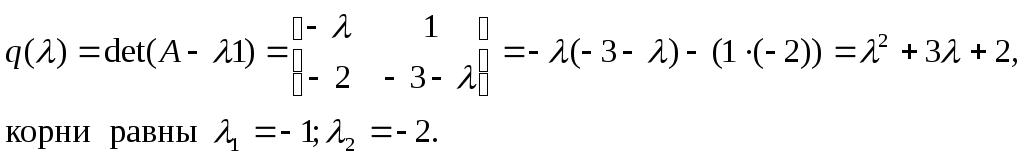
Для нахождения собственного вектора, соответствующего значению , рассмотрим систему

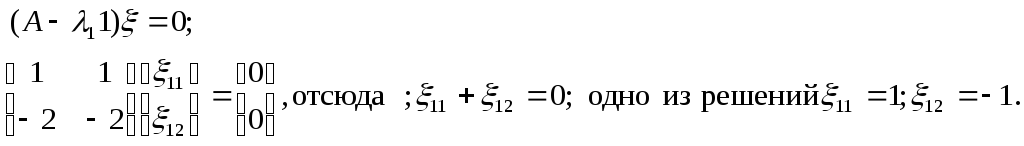
Поэтому собственный вектор, соответствующий собственному значению , имеет вид

, отметим, что он не единственный 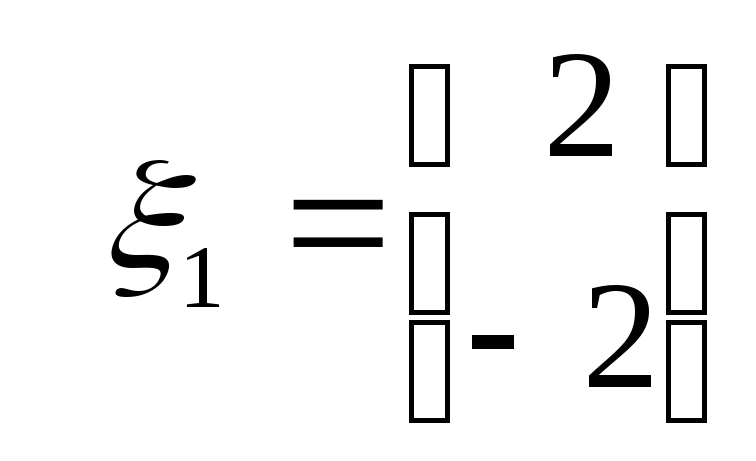и т.д. .

Для , имеем системуили

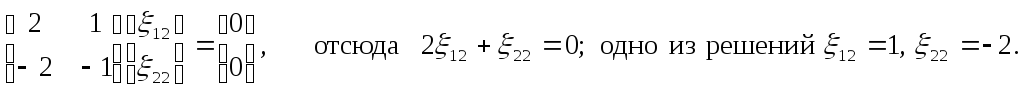
Собственный вектор, соответствующий собственному значению , имеет вид

.