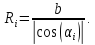- •«Теоретические основы электротехники»
- •Содержание
- •Электрическое поле заряженной электрической оси
- •Электрическое поле двух параллельных, разноименно заряженных электрических осей.
- •4. Выполнение задания «Исследование электрического поля системы двух разноименно заряженных проводящих цилиндров»
- •4.1 Определение положения электрических осей
- •4.2 Вычисление линейной плотности зарядов, потенциалов проводов и ёмкости системы
- •4.3 Построение картины поля
- •4.4 Пространственное распределение потенциала и напряжённости электрического поля
- •4.4.1. Распределение потенциалов
- •4.4.2. Распределение напряжённости электрического поля
- •4.5 Построение графиков
- •4.6 Характеристики поля в точках м1 и м2
- •4.7 Максимальные значения векторов е и d.
- •4.8 Распределение поверхностных зарядов по периметру цилиндра меньшего радиуса
- •4.10 Сила притяжения цилиндров (проводов)
-
Электрическое поле заряженной электрической оси
Электрической осью называется бесконечно длинная тонкая заряженная нить. Её электрическое поле имеет цилиндрическую симметрию: Е=Еr (r). Поэтому для расчета поля могут быть применены уравнения в интегральной форме.
Картина силовых
линий поля во всех плоскостях,
перпендикулярных оси, будет одинаковой.
Следовательно, поле является
плоскопараллельным. Выбирая, в качестве
замкнутой поверхности, некоторую
цилиндрическую поверхность произвольного
радиуса r
(рис. 1) и учитывая, что на торцевых
поверхностях такого цилиндра угол
между
 и
и
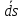 равен
равен
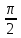 ,
получим, что на этих поверхностях
,
получим, что на этих поверхностях
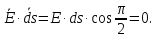

На
боковой поверхности цилиндра угол
между
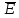 и
и
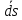 равен 0 и, следовательно,
равен 0 и, следовательно,
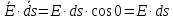 .
.
Применив теорему Гаусса к указанной замкнутой поверхности, получим:
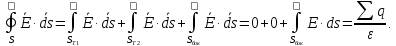
Очевидно, что в силу цилиндрической симметрии поля, во всех точках выбранной боковой поверхности цилиндра величина напряжённости поля одинакова, поэтому её можно вынести за знак интеграла. Получим:
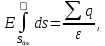
где
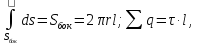
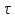 -линейная плотность
зарядов на электрической оси [Кл/м].
-линейная плотность
зарядов на электрической оси [Кл/м].
Следовательно,
E·2πr·ℓ=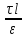 ,
,
откуда,
|
|
(1) |
С другой стороны имеем
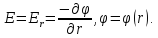
Следовательно,
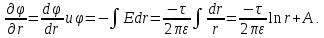
Итак
|
|
(2) |
где А - произвольная постоянная, выбор которой зависит от выбора точек нулевого потенциала.
-
Электрическое поле двух параллельных, разноименно заряженных электрических осей.
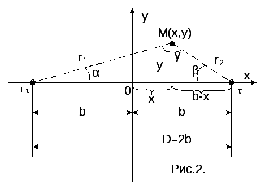
Пусть теперь даны
две параллельные, разноименно заряженные
электрические оси, расположенные на
расстоянии D=2b друг от друга(рис.2). Дано:
+τ, - τ, D, ε. Требуется определить в каждой
точке пространства
 .
Так как электрические оси бесконечно
длинные, то поле является плоскопараллельным:
потенциал и векторы поля будут одинаково
изменяться во всех плоскостях,
перпендикулярных электрическим осям.
В любой из этих плоскостей выберем
систему координат X,Y так, чтобы
электрические оси с зарядами +τ и –τ
были расположены на оси X, направленной
от +τ к –τ, а ось Y была бы посередине
между зарядами (рис.2), а ось Z направляем
вдоль электрических осей.
.
Так как электрические оси бесконечно
длинные, то поле является плоскопараллельным:
потенциал и векторы поля будут одинаково
изменяться во всех плоскостях,
перпендикулярных электрическим осям.
В любой из этих плоскостей выберем
систему координат X,Y так, чтобы
электрические оси с зарядами +τ и –τ
были расположены на оси X, направленной
от +τ к –τ, а ось Y была бы посередине
между зарядами (рис.2), а ось Z направляем
вдоль электрических осей.
В этой системе
координат будем иметь
 ,
,
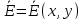 .
.
Выберем и зафиксируем
в системе координат некоторую точку
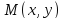 – точку наблюдения, в которой будем
определять характеристики поля.
– точку наблюдения, в которой будем
определять характеристики поля.
Точку наблюдения соединим отрезками прямых с зарядами и введем обозначения:
 – расстояние от
+τ до
– расстояние от
+τ до
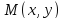 ;
;
 – расстояние от
–τ до
– расстояние от
–τ до
 ;
;
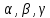 –
углы в вершинах
треугольника (
–
углы в вершинах
треугольника ( ).
).
Пользуясь
методом наложения и результатами
расчёта электрического поля одной
электрической оси, найдем потенциал в
точке наблюдения
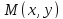 :
:
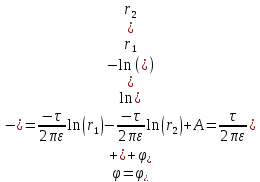
На
оси Y, где во всех точках
 ,
,
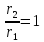 ,
ln(1)=0, получим
,
ln(1)=0, получим
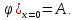 Принимая
Принимая
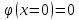 ,
получим А=0. Тогда,
,
получим А=0. Тогда,
|
|
(3) |
Следовательно,
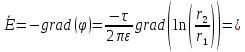
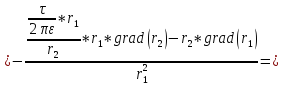
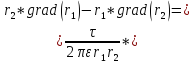
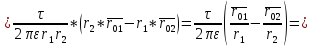
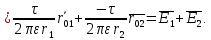
Итак,
|
|
(4) |
Где
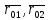 – единичные радиусы векторы, проведенные
из соответствующих электрических осей
по направлению к точке
– единичные радиусы векторы, проведенные
из соответствующих электрических осей
по направлению к точке
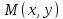 ;
;
 – напряженность
поля, обусловленная положительно
заряженной осью;
– напряженность
поля, обусловленная положительно
заряженной осью;
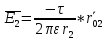 – напряженность
поля, обусловленная отрицательно
заряженной осью.
– напряженность
поля, обусловленная отрицательно
заряженной осью.
Из выражения (4)
следует, что направление вектора
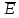 в точке
в точке
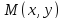 определяется геометрической суммой,
стоящей в скобках.
определяется геометрической суммой,
стоящей в скобках.
На рис.3 построена
указанная геометрическая сумма. Она
образует треугольник MNP, равный
треугольнику (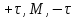 ).
Следовательно, модуль этой суммы,
соответствующий отрезку MP, равен
соответствующей ему стороне (
).
Следовательно, модуль этой суммы,
соответствующий отрезку MP, равен
соответствующей ему стороне (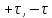 )=2b,
т.е.
)=2b,
т.е.
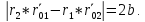

Тогда
модуль вектора
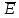 равен:
равен:
|
|
(5) |
а
его направление (по отрезку MP) относительно
оси X можно определить углом
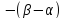 ,
где
,
где
|
|
(6) |
На рис.3 в некотором
масштабе указанным образом из точки
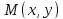 проведен вектор
проведен вектор
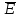 .
Там же показано его разложение на
составляющие
.
Там же показано его разложение на
составляющие
 .
.
При необходимости
можно также определить проекции вектора
 на координатные оси. Получим:
на координатные оси. Получим:

где
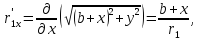
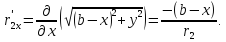
Следовательно,
|
|
(7) |
Аналогично,
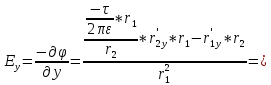
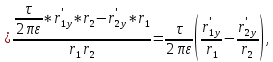
где
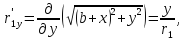
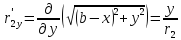 .
.
Следовательно,
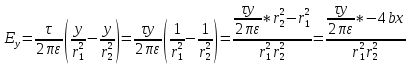 .
.
Окончательно, запишем в виде:
|
|
(8) |
Определим теперь вид линий равного потенциала. Они определяются из условия
 ,
,
которому, как следует из (3), соответствует равносильное условие
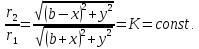
Очевидно,
что K>0 и характеризует одну линию
равного потенциала, проходящую через
точку
 .
Возводя это уравнение в квадрат, получим:
.
Возводя это уравнение в квадрат, получим:
 ,
,
Приводя это соотношение к общему знаменателю и группируя слагаемые, получим:
 .
.
Возможны два случая:
|
x=0, |
(9) |
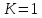 ,
тогда уравнение приводится к виду:
,
тогда уравнение приводится к виду:
представляющему собой ось Y. Это уже известная нам линия нулевого потенциала.
б)
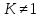 ,
тогда уравнение приводится к виду
,
тогда уравнение приводится к виду
|
|
(10) |
|
|
(11) |
|
|
(12) |
Уравнение (10)
определяет собой семейство окружностей,
центры которых находятся в точках
 (
(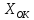 ,0),
а радиусы равны
,0),
а радиусы равны
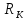 (см.рис.3).
(см.рис.3).
Так как
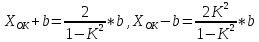 ,
то
,
то
|
|
(13) |
откуда следуют соотношения:
|
|
(14) |
(14)
|
|
(15) |
Используя (10)-(15),
можно при известных параметрах
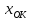 и
и
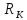 какой-либо окружности, определить
значения констант К, соответствующих
этим окружностям:
какой-либо окружности, определить
значения констант К, соответствующих
этим окружностям:
|
|
(16) |
Выражение
(16) позволяет записать потенциал
какой-либо эквипотенциальной окружности
как функцию её параметров
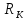 и
и
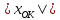 :
:
|
|
(17) |
где знак «-»
соответствует окружности, на которой
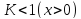 ,
а знак «+» - окружности, на которой
,
а знак «+» - окружности, на которой
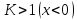 .
.
При построении семейства линий равного потенциала необходимо обеспечивать постоянство приращения потенциала при переходе от любой линии равного потенциала к другой(соседней), т.е.
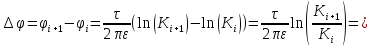
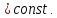
Следовательно, числа К при возрастании порядкового номера i-той линии должны изменяться в геометрической прогрессии со знаменателем
|
|
(18) |
а
|
|
(19) |
На рис.4 показан
пример построения семейства линий
равного потенциала при b=40мм, n=7(количество
линий равного потенциала) и

Из 7-ми линий
равного потенциала одна – это ось Y,
где
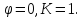 От этой линии по три располагаются
слева и справа от оси Y (симметрично,
если принять, что минимальные радиусы
линий равного потенциала одинаковы –
по 10 мм). Поэтому достаточно построить
картину поля, например, справа от оси
Y, тогда левая часть картины поля будет
ей симметрична.
От этой линии по три располагаются
слева и справа от оси Y (симметрично,
если принять, что минимальные радиусы
линий равного потенциала одинаковы –
по 10 мм). Поэтому достаточно построить
картину поля, например, справа от оси
Y, тогда левая часть картины поля будет
ей симметрична.
Зная b и
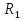 ,
по (14) найдем:
,
по (14) найдем:
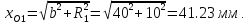
Тогда константа
 ,
соответствующая первой окружности
равного потенциала, будет равна( по
(16)):
,
соответствующая первой окружности
равного потенциала, будет равна( по
(16)):
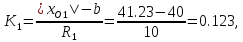
или
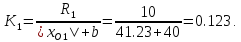
Так как
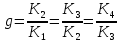 ,
,
то


где
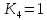 (константа
оси Y).
(константа
оси Y).
Следовательно,
 .
.
Далее находим:
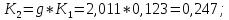
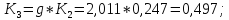
Проверка:
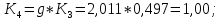
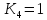 .
Верно.
.
Верно.
По (12) и (14) находим:



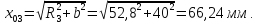
По найденным
параметрам окружностей (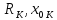 )
строим (рис.4) искомые линии равного
потенциала.
)
строим (рис.4) искомые линии равного
потенциала.
Соотношение (13)
приводит нас ещё к одному замечательному
выводу о том, что любая окружность
 (рис.4), проведённая через электрические
оси (центры таких окружностей лежат на
оси Y), является силовой линией поля.
(рис.4), проведённая через электрические
оси (центры таких окружностей лежат на
оси Y), является силовой линией поля.
Действительно,
зафиксируем точку M(x,y) пересечения
окружности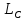 с какой-либо окружностью равного
потенциала, например с окружностью
с какой-либо окружностью равного
потенциала, например с окружностью
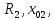 центр которой находится в точке
центр которой находится в точке
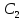 .
Тогда отрезки +τС2
и –τС2,
равные соответственно
.
Тогда отрезки +τС2
и –τС2,
равные соответственно
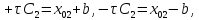
можно рассматривать
как отрезки секущей для окружности
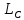 .
Из геометрии известно, что их произведение
равно квадрату соответствующего отрезка
касательной к этой окружности, но оно
по (13) равно
.
Из геометрии известно, что их произведение
равно квадрату соответствующего отрезка
касательной к этой окружности, но оно
по (13) равно
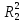 .
Следовательно, отрезок
.
Следовательно, отрезок
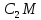 – есть касательная к окружности
– есть касательная к окружности
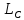 и в то же время
и в то же время
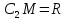 – есть радиус окружности
– есть радиус окружности
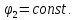 Следовательно, обе окружности пересекаются
под прямым углом, но тогда
Следовательно, обе окружности пересекаются
под прямым углом, но тогда
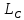 – есть силовая линия поля, т.к.
– есть силовая линия поля, т.к.
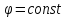 – равнопотенциальная: силовые и
равнопотенциальные линии пересекаются
под прямым углом. Таким образом, линии
напряженности электрического поля
– равнопотенциальная: силовые и
равнопотенциальные линии пересекаются
под прямым углом. Таким образом, линии
напряженности электрического поля
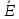 двух параллельных, разноименно заряженных
электрических осей представляют собой
дуги окружностей, начинающихся на +τ и
заканчивающихся на –τ.
двух параллельных, разноименно заряженных
электрических осей представляют собой
дуги окружностей, начинающихся на +τ и
заканчивающихся на –τ.
Поле подразделяется
на трубки равного потока, если центры
окружностей
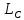 образуются пучком прямых, проведенных
из +τ через угол
образуются пучком прямых, проведенных
из +τ через угол
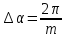 ,
где m – общее число силовых линий.
,
где m – общее число силовых линий.
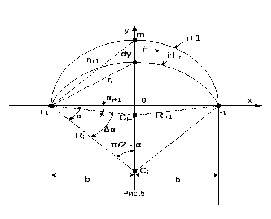
Покажем это,
определяя поток
 сквозь поперечное сечение mn трубки
потока (между двумя соседними силовыми
линиями, изображёнными на рис.5)
сквозь поперечное сечение mn трубки
потока (между двумя соседними силовыми
линиями, изображёнными на рис.5)
Получим:
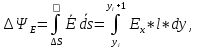
где по (7) имеем:
 .
.
Следовательно,
|
|
(20) |
где
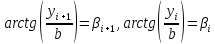 – вписанные в окружности
– вписанные в окружности
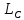 углы, опирающиеся на центральные углы
углы, опирающиеся на центральные углы
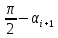 и
и
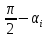 соответственно.
соответственно.
Поэтому
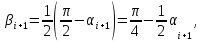
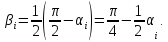
Следовательно,

Тогда
|
|
(21) |
Поэтому
условию
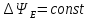 равносильно условие
равносильно условие
|
|
(22) |
Если при построении
картины поля изменять угол
 через равные интервалы
через равные интервалы
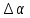 на промежутке
на промежутке
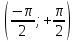 ,
то получим полную картину поля, состоящую
из трубок равного потока (21). При этом
центры Ci
окружность
силовых линий получаются как точки
пересечения соответствующих лучей (
,
то получим полную картину поля, состоящую
из трубок равного потока (21). При этом
центры Ci
окружность
силовых линий получаются как точки
пересечения соответствующих лучей (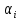 )
с осью OY, т.е. координаты центров
окружностей LC
будут равны:
)
с осью OY, т.е. координаты центров
окружностей LC
будут равны:
|
|
(23) |
а их радиусы
|
|
(24) |
Если
принимать
 ,
то количество силовых линий будет
равно
,
то количество силовых линий будет
равно
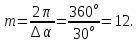
Полное построение картины поля при n=7, m=12, b=40 мм представлено на рисунке 4.
3. Обоснование возможности использования результатов теории электрического поля двух параллельных разноименно заряженных электрических осей для исследования электрического поля параллельных, разноименно заряженных цилиндров.
Общей задачей
расчёта любого электрического поля, в
том числе и заданной системы заряженных
цилиндров, является определение
напряженности поля
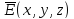 как функции координат. Такая задача
полностью решается отысканием потенциала
как функции координат. Такая задача
полностью решается отысканием потенциала
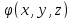 ,
так как
,
так как

В задании дано
расположение и форма проводящих тел и
разность потенциалов (напряжение) между
ними. Такая задача относится к типу
задач Дирихле, которые в общем случае
считаются трудными. Их решение сводится
к подбору функции
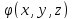 ,
которая должна удовлетворять уравнению
Лапласа
,
которая должна удовлетворять уравнению
Лапласа
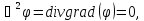
так как объемных
зарядов ρ в пространстве между цилиндрами
нет. Поскольку рассматриваемое поле
можно отнести к типу плоскопараллельных
(l>>D), то
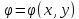 и уравнение Лапласа в прямоугольной
системе координат будет иметь вид
и уравнение Лапласа в прямоугольной
системе координат будет иметь вид
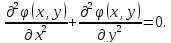
Решение этого уравнения должно удовлетворять следующим граничным условиям:
-
На поверхности проводящих цилиндров

-
Внутри проводящих цилиндров

Однако в прямоугольной системе координат ни одна координатная поверхность не совпадает с цилиндрическими поверхностями проводников, что осложняет применение граничных условий при определении постоянных интегрирования уравнения Лапласа.
Применение цилиндрической системы координат не решает этой проблемы, так как оси цилиндров разнесены на расстояние D. Поэтому выбор системы координат, совмещенной с одним из проводов, не обеспечивает упрощения в процедуре применения граничных условий.
Однако при решении рассматриваемой задачи можно воспользоваться результатами, полученными при исследовании электрического поля двух параллельных разноименно заряженных электрических осей.
Действительно, картина поля двух параллельных заряженных электрических осей состоит из семейства окружностей силовых линий и линий равного потенциала. Мы можем некоторые эквипотенциальные окружности (в пространстве это цилиндрические поверхности) заменить проводящими цилиндрами. При этом, на основании теоремы единственности решения, можно утверждать, что в пространстве между такими цилиндрами решение не изменится.
При этом можно решить столько новых задач, сколько на картине поля имеется различных по взаимному расположению пар равнопотенциальных поверхностей, которые можно рассматривать как поверхности проводников.
Это могут быть следующие задачи:
А) Двухпроводная линия с проводами одинакового радиуса

Б) Двухпроводная линия с проводами разного радиуса (наша задача)

В) Несоосные цилиндры, находящиеся один в другом
Г) Система цилиндр – плоскость
Во всех этих задачах должны быть известны радиусы цилиндров (заданные поверхности равного потенциала), их взаимное положение, заряды проводов или напряжение между ними. При этом задача сводится к определению положения смещенных электрических осей.

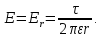
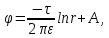
 .
.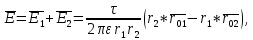
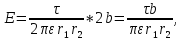
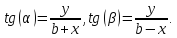
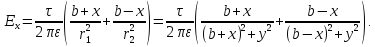
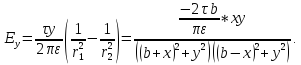
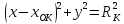 ,
,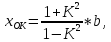

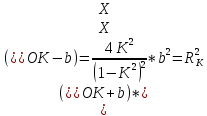 ,
,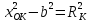 ,
, 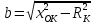 ,
,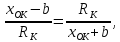
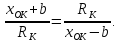
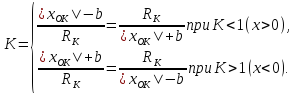
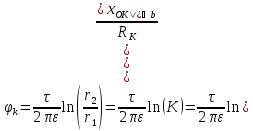
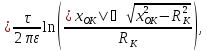
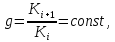
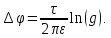
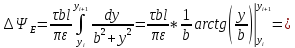
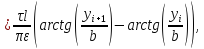
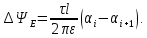
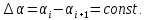
 ,
,