3. Двойственная задача.

Двойственная задача формулируется следующим образом.

Определить оценку единицы каждого вида ресурсов, чтобы при заданных объемах ресурсов , прибыли , минимизировать оценку всех ресурсов торгового предприятия, затраченных на организацию торгового процесса.

Запишем математическую модель двойственной задачи.

Определить, который удовлетворяет ограничениям

и доставляет минимальное значение целевой функции

Ограничения показывают, что стоимость всех ресурсов, затраченных на продажу единицы группы товаров, должна быть не меньше прибыли, получаемой при реализации единицы группы товаров, а общая стоимость всех ресурсов должна быть минимизировать.

Для симметричной пары задач двойственная задача по отношению к исходной, составляется согласно следующим правилам:

1. Число переменных в двойственной задаче равно числу ограничений в прямой задаче.

2. Матрица коэффициентов системы ограничений двойственной задачи получается из матрицы коэффициентов системы ограничений прямой задачи путем транспонирования.

3. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи.

4. Свободными членами системы ограничений двойственной задачи являются коэффициенты функции цели прямой задачи.

5. На каждую переменную двойственной задачи накладывается условие не отрицательности. Двойственная задача решается на минимум, если целевая функция прямой задачи задается на максимум, и наоборот.

6. Двойственная задача решается на минимум, если целевая функция прямой задачи задаётся на максимум, и наоборот.

7. Коэффициентами функции цели двойственной задачи служат свободные члены системы ограничений прямой задачи.

Решение прямой задачи дает оптимальные объемы в структуру товарооборота торгового предприятия, а решение двойственной - оптимальную систему оценок ресурсов, используемых для реализации товаров.

Установим сопряженные пары переменных прямой и двойственной задач. Запишем переменные задач в двух строчках. В первой располагаем переменные по порядку номеров: сначала основные, затем -дополнительные, а во. второй строке запишем переменные двойственной задачи: сначала дополнительные, затем - основные.

основные дополнительные

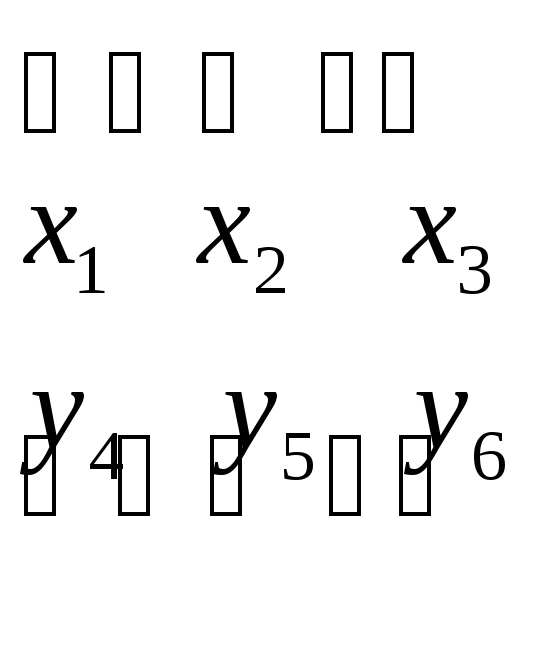
дополнительные основные

Согласно сопряженным парам переменных из решения прямой задачи можно получить решение двойственной, не решая ее, и наоборот, из решения двойственной задачи можно получить решения прямой.

Составим, например, двойственную задачу к прямой задаче, которая решена выше симплексным методом.

Определить, который удовлетворяет условиям -ограничениям :

и обеспечивает минимальное значение целевой функции

Z()=1100y₁+120y₂+8000y₃ min

Таким образом, оптимальный план двойственной задачи имеет вид:

= (23,75; 12,5; 0; 0; 0; 5,75) =27625

По этим данным проводится анализ оптимального плана двойственной задачи по оценке ресурсов, используемых для реализации товаров.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Как сформулировать экономическую постановку двойственной задачи к задаче планирования торгового процесса?

2. Как записывается математическая модель прямой и двойственной задач?

3. Каков план построения двойственной задачи?

4. Как определяется сопряженные пары переменных : прямой и двойственной задач?

4. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Транспортная задача заключается в определении оптимального плана перевозок некоторого однородного груза из m пунктов от­правления в пунктов потребления .

Рассмотрим транспортную задачу, где в качестве критерия оптимальности является стоимость перевозок всего груза, которая должна быть минимальной.

Введем обозначения:

запасы груза в ом пункте отправления ;

величина заказа на этот груз в ом пункте назначения ;

стоимость перевозки единицы груза из А го пункта отправления в В ый пункт потребления (тариф перевозок);

- количество груза, доставленного из пункта в пункт, 0 •

Определить план перевозок груза из пунктов отправления в пункты назначения так, чтобы: вывести все грузы от поставщиков; удовлетворить заявки каждого потребителя; обеспечить минимальные транспортные расходы на перевозку груза.

Все исходные данные транспортной задачи можно записать в виде транспортной таблицы 4.

Таблица 4

Пункты отправления	Пункты назначения						Запасы
			…		…
			…		…
			…		…
…	…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…	…
			…		…
Заявки			…		…

где- суммарный запас груза у поставщиков;

- суммарная величина заявок потребителей.

Математическая постановка транспортной задачи заключается в определении матрицы

', ,которая удовлетворяет следующим условиям:

а) Всякое неотрицательное решение системы линейных уравнений, определяемое матрицей

', называется допустимым планом транспортной задачи.

б) Ранг матрицы, составленный из коэффициентов при неизвестных системы линейных уравнений транспортной задачи, на единицу меньше числа уравнений, т.е. равен . Следовательно, число линейно независимых уравнений равно , они образуют базис, а соответствующие им переменных будут являться базисными.

в) Допустимый план транспортной задачи, имеющий не более отличных от нуля величин , называется опорным.

г) Если в опорном плане число отличных от нуля компонент равно в точности , то план является невырожденным, если меньше, то план называется вырожденным.

д) План ', при котором функция 4 принимает свое минимальное значение, называется оптимальным планом транспортной задачи.

е) Для решения транспортной задачи необходимо и достаточно, чтобы суммарные запасы груза в пунктах отправления были равны сумме заявок пунктов назначения:

ж) Модель транспортной задачи, удовлетворяющая этому условию, называется закрытой. Если же указанное условие не выполняется, то модель называется открытой.

В случае превышения запаса над заявками:

вводится фиктивный пункт назначения с потребностью

= и соответствующие тарифы считаются равными нулю: .

При вводится фиктивный (m+1) пункт отправления с запасом груза =, и тарифы принимаются равными нулю:

Рассмотрим один из методов построение первого опорного плана - метод наименьших тарифов.

з) Наилучшим элементом матрицы тарифов называется наименьший тариф, если задача поставлена на минимум, наибольший тариф - если задача поставлена на максимум целевой функции.

Алгоритм построения первого опорного плана методом наименьшей стоимости включает следующие этапы.

1. Среди тарифов находится наименьший.

2. Клетку с выбранным тарифом заполняем максимально возможным объемом груза с учетом ограничений по строке и столбцу, при этом либо весь груз вывозится от соответствующего поставщика, либо полностью удовлетворяется заявка потребителя. Строка или столбец таблицы вычеркивается и в дальнейшем распределении не участвует.

3. Из оставшихся тарифов вновь находим наилучший, и процесс продолжается до тех пор, пока не будет распределен весь груз.

Если модель транспортной задачи открытая и введены фиктивный поставщик или потребитель, то распределение осуществляется сначала для действительных поставщиков и потребителей, и в последнюю очередь нераспределенный груз направляется от фиктивного поставщика или к фиктивному потребителю.

Дальнейшее улучшение первого опорного плана и получение оптимального плана производим методом потенциалов.

и) План транспортной задачи будет являться оптимальным, если существует система m+n чисел называемых потенциалами, удовлетворяющая условиям:

- для занятых клеток, где >0

для свободных клеток, где =0

при решении задачи на минимум, а при решении задачи на максимум:

для занятых клеток, где >0

для свободных клеток, где =0,

Потенциалы и являются переменными двойственной транспортной задачи и обозначают оценку единицы груза в пунктах отправления и назначения соответственно.

Введем обозначение оценки свободной клетки таблицы:

Если среди оценок нет отрицательная (задача поставлена на минимум), то опорный план является оптимальным и все сво­бодные клетки потенциальны.

Алгоритм метода потенциалов включает следующие этапы.

1. Построение первого опорного плана.

2. Проверка вырожденности плана.

Потенциалы и могут быть рассчитаны только для невырожденного плана. Если число занятых клеток в опорном плане меньше, чем , то вносим нуль в одну из свободных клеток таблицы так, чтобы общее число занятых клеток стало равным . Нуль вводят в клетку с наилучшим тарифом одного из одновременно вычеркиваемых рядов таблицы. При этом фиктивно занятая нулем клетка не должна об­разовывать замкнутого контура с другими клетками таблицы.

3. Определение значения функции цели путем суммирования произведений тарифов (удельных затрат) на объем перевозимого груза по всем занятым клеткам таблицы.