3. Конгруентність многочленів над скінченним полем

Для многочленів над скінченним полем, як і для чисел, можна ввести поняття конгруенції.

Означення. Нехай , , – многочлени з . Многочлен називається конгруентним многочлену за модулем многочлена , якщо різниця ділиться на . Цей факт позначають так:

Останнє співвідношення називається конгруенцією многочленів за модулем многочлена .

Лишок многочлена за модулем многочлена дорівнює остачі від ділення на . Очевидно, у такому випадку при діленні на многочлени і дають однакову остачу. Процес переходу від до називається зведенням за модулем .

Приклад 6. Знайти лишок многочлена за модулем 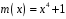над полем .

Розв’язання. У прикладі 3 знайдено

За означенням конгруентності многочленів маємо:

.

Приклад 7. Знайти лишок многочлена за модулем над полем .

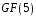Розв’язання. У прикладі 4 знайдено

За означенням конгруентності многочленів маємо:

.

4. Незвідні многочлени над скінченним полем

Означення. Многочлен називається незвідним над полем або у кільці , якщо рівність , де , 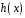– многочлени над , виконується тільки за умови, що якийсь з многочленів чи є сталим.

Незвідність многочленів аналогічна простоті цілих чисел. Незвідний многочлен не ділиться ні на який многочлен меншого степеня. Зокрема, всякий многочлен першого степеня є незвідним. Для незвідності многочлена степеня 2 або 3 над полем необхідно і достатньо, щоб він не мав коренів в полі .

Приклад 8. Знайти всі незвідні многочлени степенів 2 та 3 над полем .

Розв’язання. З множини всіх многочленів відповідного степеня, які належать кільцю , вилучимо ті, які не мають коренів в полі . Ними виявляються один незвідний многочлен степеня 2 і два незвідні многочлени степеня 3 та .

Незвідні многочлени відіграють велику роль в побудові кільця , тому що кожен многочлен з можна єдиним способом подати у вигляді добутку незвідних нормованих многочленів над полем .

.

де , .

Розкладання многочлена на добуток незвідних нормованих многочленів відбувається за допомогою тотожних перетворень, які використовують властивості операцій в кільці многочленів: комутативність, асоціативність додавання і множення многочленів і дистрибутивність множення відносно додавання: винесення спільного множника за дужки, групування доданків, застосування формул скороченого множення тощо. Також можна скористатися методом невизначених коефіцієнтів, в основі якого лежать твердження:

Приклад 9. Розкласти многочлен на добуток незвідних множників над полем .

Розв’язання. Скористаємося методом невизначених коефіцієнтів. Оскільки многочлен третього степеня розкладається на добуток лінійного і квадратичного многочленів, то будемо шукати многочлени і такі, що справедлива рівність:

або

.

Прирівнюючи коефіцієнти при однакових степенях в лівій і правій частинах рівності, отримуємо систему для визначення невідомих коефіцієнтів. Розв’язуючи цю систему над полем 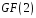, будемо мати:

Отже,

.

Для криптографічних цілей особливо важливі многочлени, незвідні над скінченним полем простої характеристики .