- •Лекція № 8 Тема: Многочлени над скінченними полями
- •1. Кільце многочленів над скінченним полем
- •2. Операції в кільці многочленів над скінченним полем.
- •3. Конгруентність многочленів над скінченним полем
- •4. Незвідні многочлени над скінченним полем
- •Властивості незвідних многочленів над полем :
- •5. Скінченні поля на базі кілець многочленів
- •6. Примітивні многочлени
- •7. Побудова скінченного поля
Властивості незвідних многочленів над полем :
-
Будь-який незвідний многочлен степеня
 над полем
над полем
 є дільником многочлена
є дільником многочлена
 .
. -
Незвідний многочлен степеня
 над полем
над полем
 є дільником многочлена
є дільником многочлена
 тоді і тільки тоді, коли
тоді і тільки тоді, коли
 .
. -
Число
 нормованих незвідних многочленів
степеня
нормованих незвідних многочленів
степеня
 над полем
над полем
 дорівнює
дорівнює
 ,
де сума береться за всіма додатними
дільниками
,
де сума береться за всіма додатними
дільниками
 числа
числа
 ,
,
 – функція Мебіуса:
– функція Мебіуса:

Приклад
10.
Знайти
число нормованих незвідних многочленів
степеня 4 над полем
 .
.
Розв’язання.
Додатні дільники числа
 є 1, 2, 4. Отже
є 1, 2, 4. Отже

 .
.
Отже,
існує 3 нормованих незвідних многочленів
степеня 4 над полем
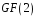 .
.
Щоб
знайти всі незвідні многочлени даного
степеня
 над полем
над полем
 ,
треба:
,
треба:
-
Знайти всі звідні нормовані многочлени даного степеня
 над полем
над полем
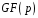 .
. -
Вилучити отриману множину з множини всіх можливих нормованих многочленів степеня
 над полем
над полем
 .
.
Зауваження.
При великих
 і
і
 цей спосіб непридатний.
цей спосіб непридатний.
Приклад
11
Знайти
всі незвідні многочлени степеня 4 над
полем
 .
.
Розв’язання.
Число
елементів поля
 дорівнює
дорівнює
 .
Число різних многочленів четвертого
степеня над полем
.
Число різних многочленів четвертого
степеня над полем
 дорівнює
дорівнює
 :
:
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,
 ,
,  ,
,  ,
,  ,
,
 ,
,  ,
,  ,
,
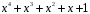 .
.
Всі
потрібні звідні многочлени можна
утворити, знайшовши добутки нормованих
многочленів
 або
або
 ,
де всі
,
де всі
 .
Після вилучення із списку всіх подібних
добутків дістанемо всі незвідні
многочлени степеня 4 над полем
.
Після вилучення із списку всіх подібних
добутків дістанемо всі незвідні
многочлени степеня 4 над полем
 :
:
 ,
,
 ,
,
 .
.
Їх 3, як було визначено раніше.
Розглянемо тепер питання про множину коренів незвідного многочлена над скінченним полем. На це важливе питання дають відповідь наступні теореми.
Лема.
Нехай
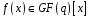 – незвідний многочлен степеня
– незвідний многочлен степеня
 над полем
над полем .
Тоді
.
Тоді
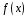 ділить многочлен
ділить многочлен
 тоді і тільки тоді, коли число
тоді і тільки тоді, коли число
 ділить
ділить
 .
.
Теорема
Галуа.
Якщо
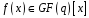 – незвідний многочлен степеня
– незвідний многочлен степеня
 над полем
над полем
 ,
то в полі
,
то в полі
 міститься будь-який корінь
міститься будь-який корінь
 многочлена
многочлена
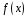 .
Більше того, всі корені многочлена
.
Більше того, всі корені многочлена
 прості (згадаємо, що корінь простий,
якщо його кратність
прості (згадаємо, що корінь простий,
якщо його кратність
 )
і ними є
)
і ними є
 різних елементів
різних елементів
 ,
,
 ,
,
 ,..,
,..,
 поля
поля
 .
.
З цієї теореми випливають наступні факти:
1.
Незвідний многочлен
 над полем
над полем
 цілком розкладається в цьому полі,
тобто, поле
цілком розкладається в цьому полі,
тобто, поле
 є полемо розкладання над полем
є полемо розкладання над полем
 .
.
2.
Поля розкладання будь-яких двох незвідних
многочленів одного й того самого степеня
з кільця
 ізоморфні.
ізоморфні.
3.
Кожне скінченне розширення
 скінченного поля
скінченного поля
 є нормальним розширенням, тобто воно
має властивість, що кожен незвідний
многочлен з
є нормальним розширенням, тобто воно
має властивість, що кожен незвідний
многочлен з
 що має хоча б один корінь в полі
що має хоча б один корінь в полі
 ,
розкладається в цьому полі на лінійні
співмножники.
,
розкладається в цьому полі на лінійні
співмножники.
4. Будь-яке скінченне поле є досконалим полем, тобто має властивість: кожний незвідний многочлен над цим полем має тільки прості корені.
5. Скінченні поля на базі кілець многочленів
Скінченні поля будуються з кілець многочленів так само, як вони будувалися з кілець класів лишків.
Означення.
Для довільного зведеного многочлена
 ненульового степеня над полем
ненульового степеня над полем
 кільцем
многочленів за модулем
кільцем
многочленів за модулем
 називається множина всіх многочленів
над цим полем, степені яких не перевищують
степеня самого многочлена
називається множина всіх многочленів
над цим полем, степені яких не перевищують
степеня самого многочлена
 ,
з операціями додавання і множення
многочленів за модулем
,
з операціями додавання і множення
многочленів за модулем
 .
Позначають
.
Позначають
 .
.
Довільний
елемент
 з кільця
з кільця
 відображається в елемент кільця
відображається в елемент кільця
 за допомогою функції
за допомогою функції
 ,
де
,
де
 – остача від ділення многочлена
– остача від ділення многочлена
 на модуль
на модуль
 .
Два елементи
.
Два елементи
 і
і
 з кільця
з кільця
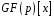 ,
що відображаються в один й той самий
елемент з кільця
,
що відображаються в один й той самий
елемент з кільця
 ,
будуть конгруентними:
,
будуть конгруентними:
 .
.
(тоді
 для деякого многочлена
для деякого многочлена
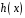 )
)
Приклад
12.
Побудувати кільце многочленів за модулем
 над полем
над полем
 .
.
Розв’язання.
Кільце
 многочленів за модулем
многочленів за модулем
 складається з усіх многочленів над
полем
складається з усіх многочленів над
полем
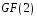 ,
степінь яких – не вище 2, тобто з елементів
,
степінь яких – не вище 2, тобто з елементів
 .
.
У цьому кільці множення виконується, наприклад, таким чином:
 ,
,
де
враховано, що
 у полі
у полі
 .
.
Кільце
класів лишків цілих чисел за модулем
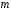 утворює поле тільки коли
утворює поле тільки коли
 ,
де
,
де
 – просте число. Так само, кільце
– просте число. Так само, кільце
 утворює
поле тільки коли многочлен
утворює
поле тільки коли многочлен
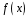 – незвідний.
– незвідний.
Теорема
(необхідна і достатня умова перетворення
кільця многочленів на поле).
Кільце многочленів
 за модулем
за модулем буде полем тоді і тільки тоді, коли
многочлен
буде полем тоді і тільки тоді, коли
многочлен
 – нормований і незвідний.
– нормований і незвідний.
Якщо
над полем Галуа
 знайдено нормований незвідний многочлен
степеня
знайдено нормований незвідний многочлен
степеня
 ,
то на основі викладеної теорії можна
побудувати поле Галуа, елементи якого
зображуються многочленами над
,
то на основі викладеної теорії можна
побудувати поле Галуа, елементи якого
зображуються многочленами над
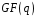 степенів не вище
степенів не вище
 .
Всього існує
.
Всього існує
 таких многочленів, тому і поле буде
складатися з
таких многочленів, тому і поле буде
складатися з
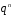 елементів.
елементів.
Приклад
13.
Побудувати поле
 як поле многочленів за модулем многочлена
як поле многочленів за модулем многочлена
 над полем
над полем
 .
.
Розв’язання.
Многочлен
 є незвідним над полем
є незвідним над полем
 ,
тому що він другого степеня і не має
коренів в даному полі. Поле многочленів
за цим модулем складається з
,
тому що він другого степеня і не має
коренів в даному полі. Поле многочленів
за цим модулем складається з
 елементів: 0,1,
елементів: 0,1,
 ,
,
 ,
які також визначені над полем
,
які також визначені над полем
 і степені яких менші за степінь многочлена
і степені яких менші за степінь многочлена
 .
Для побудови таблиць Келі для елементів
поля
.
Для побудови таблиць Келі для елементів
поля
 виконаємо операції додавання і множення
над його елементами і у разі необхідності
зведемо результати за модулем
виконаємо операції додавання і множення
над його елементами і у разі необхідності
зведемо результати за модулем
 .
Дістанемо такі таблиці:
.
Дістанемо такі таблиці:
|
|
0 |
1 |
|
|
||
|
0 |
0 |
0 |
0 |
0 |
||
|
1 |
0 |
1 |
|
|
||
|
|
0 |
|
0 |
1 |
||
|
|
0 |
|
1 |
|
||
|
+ |
0 |
1 |
|
|
|
0 |
0 |
1 |
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
0 |
1 |
|
|
|
|
1 |
0 |
Після побудови таблиць можна замінити позначення елементів через многочлени на двійкові, цілочислові або інші бажані позначення.
Позначення
елементів поля
 за допомогою
за допомогою
|
Многочленів |
Двійкових чисел |
Цілих чисел |
Степенів
|
|
0 |
00 |
0 |
0 |
|
1 |
01 |
1 |
|
|
|
10 |
2 |
|
|
|
11 |
3 |
|
Зауваження. Одним з способів перевірки незвідності многочленів, які використовуються як модулі для побудови скінченних полів, є метод спроб і помилок, хоча безпосередня перевірка всіх можливих розкладань многочленів високих степенів ускладнена. На практиці застосовують готові таблиці незвідних многочленів над різними скінченними полями.
Приклад
14. Елементи
поля Галуа
 – двійкові послідовності довжиною
– двійкові послідовності довжиною
 бітів, зручно розглядати у вигляді
многочленів. Наприклад, байт з 8 бітів
10010101
можна зобразити многочленом
бітів, зручно розглядати у вигляді
многочленів. Наприклад, байт з 8 бітів
10010101
можна зобразити многочленом
 .
.