
- •Система отсчета. Кинематика материальной точки. Траектория и путь. Перемещение, скорость и ускорение материальной точки.
- •Криволинейное движение. Скорость и ускорение (нормальное, тангенциальное) при криволинейном движении.
- •Прямолинейное (равномерное и равноускоренное) движение. Графики зависимости координаты и скорости от времени.
- •Движение материальной точки по окружности. Угловая скорость и угловое ускорение. Равномерное и равноускоренное вращательные движения. Связь между линейными и угловыми величинами.
- •Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности Галилея, преобразования Галилея. Закон сложения скоростей.
- •Взаимодействие тел, сила, масса. Второй закон Ньютона. Виды силовых взаимодействий. Силы упругости, трения, тяготения.
- •Третий закон Ньютона. Импульс. Изолированная система. Закон сохранения импульса.
- •Неинерциальные системы отсчета. Силы инерции в поступательных и во вращательных неинерциальных системах отсчета.
- •Центр масс. Теорема о движении центра масс.
- •Движение тела переменной массы. Уравнение Мещерского.
- •Движение в центральном поле сил. Законы Кеплера и закон всемирного тяготения.
- •Консервативные и неконсервативные силы. Работа консервативных сил. Потенциальная энергия.
- •Связь между силой и потенциальной энергией. Потенциальные энергии силы тяжести, силы упругости и силы гравитационного взаимодействия.
- •Механическая работа и кинетическая энергия. Механическая энергия системы тел. Закон сохранения механической энергии.
- •Соударение двух тел. Абсолютно упругий и абсолютно неупругий удар.
- •Момент импульса и момент силы относительно неподвижного начала. Уравнение моментов.
- •Уравнение моментов. Закон сохранения момента импульса.
- •Момент импульса и момент силы относительно неподвижной оси. Уравнение динамики вращательного движения относительно неподвижной оси.
- •Инерция при вращательном движении. Момент инерции. Кинетическая энергия твердого тела при вращательном движении.
- •Моменты инерции симметричных тел (цилиндр, шар). Теорема Штейнера. Пример применения.
- •(21)Гидростатика. Закон Паскаля. Закон Архимеда. Основное уравнение гидростатики.
- •(22) Стационарное движение идеальной жидкости. Уравнение Бернулли.
- •Гармонические колебания. Основные характеристики гармонических колебаний: амплитуда, фаза, частота, период.
- •Комплексная форма гармонических колебаний. Сложение гармонических колебаний одинаковых и близких частот. Биения.
- •Гармонический осциллятор. Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов: пружинный, физический и математический маятники.
- •Затухающие колебания. Коэффициент затухания, время релаксации. Логарифмический декремент затухания.
- •Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс. Резонансные характеристики осциллятора (добротность, избирательность).
- •29 Принцип суперпозиции. Интерференция волн. Стоячие волны.
- •(30) Эффект Доплера. Его применение.
- •28) Классическое волновое уравнение. Бегущие волны. Гармоническая бегущая волна, ее характеристики (длина волны, частота и др.).
-
Комплексная форма гармонических колебаний. Сложение гармонических колебаний одинаковых и близких частот. Биения.
Гармонические колебания величины s описываются уравнение типа s =A cos (w0 t +j)
w0 - круговая (циклическая) частота,
j - начальная фаза колебания в момент времени t=0
(w0 t +j) - фаза колебания в момент времени t
![]() Согласно
формуле Эйлера, для комплексных чисел
Согласно
формуле Эйлера, для комплексных чисел![]() где
где
![]() -мнимая
единица. Поэтому уравнение гармонического
колебания можно записать в
-мнимая
единица. Поэтому уравнение гармонического
колебания можно записать в
к![]() омплексной
форме:
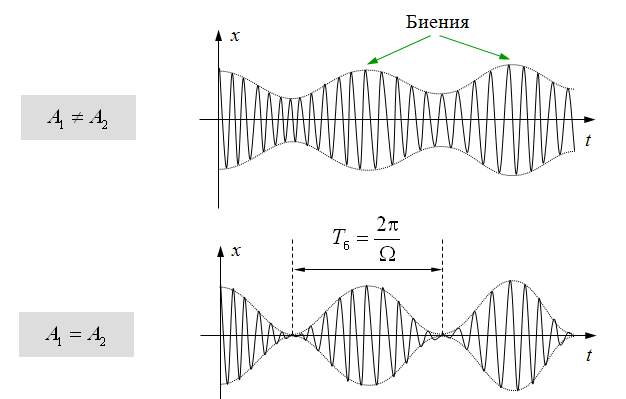
Бие́ния
— явление, возникающее при наложении
двух гармонических колебаний близкой
частоты и выражающееся в периодическом
уменьшении и увеличении амплитуды
суммарного сигнала. Частота изменения
амплитуды суммарного сигнала равна
разности частот двух исходных сигналов.
омплексной
форме:
Бие́ния
— явление, возникающее при наложении
двух гармонических колебаний близкой
частоты и выражающееся в периодическом
уменьшении и увеличении амплитуды
суммарного сигнала. Частота изменения
амплитуды суммарного сигнала равна
разности частот двух исходных сигналов.
Биения возникают от того, что один из двух сигналов постоянно отстаёт от другого по фазе и в те моменты, когда колебания происходят синфазно, суммарный сигнал оказывается усилен, а в те моменты, когда два сигнала оказываются в противофазе, они взаимно гасят друг друга. Эти моменты периодически сменяют друг друга по мере того как нарастает отставание.

![]()
-
Гармонический осциллятор. Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов: пружинный, физический и математический маятники.
Гармонический
осциллятор
— это система, которая при смещении из
положения равновесия испытывает действие
возвращающей силы
![]() ,
пропорциональной смещению
,
пропорциональной смещению
![]() :
:
![]()
Динамика
простого гармонического движения.
Для
колебания в одномерном пространстве,
учитывая Второй закон Ньютона (F =
m d²x/dt²)
и закон Гука (F
= −kx,
как описано выше), имеем линейное
дифференциальное уравнение второго
порядка:
![]() где m —
это масса
тела,
x —
его перемещение относительно положения
равновесия, k —
постоянная (коэф. жесткости пружины).
Решение этого дифференциального
уравнения является синусоидальным;
одно из решений таково: x(t)
= Acos(ωt
+ φ)
где m —
это масса
тела,
x —
его перемещение относительно положения
равновесия, k —
постоянная (коэф. жесткости пружины).
Решение этого дифференциального
уравнения является синусоидальным;
одно из решений таково: x(t)
= Acos(ωt
+ φ)
![]()
![]()
Примеры:
Груз
на пружине. Масса
m,
прикреплённая к пружине с постоянной
жёсткостью k
является примером простого гармонического
движения в пространстве. Формула
![]() показывает, что период колебаний не
зависит от амплитуды и ускорения
свободного падения.
показывает, что период колебаний не
зависит от амплитуды и ускорения
свободного падения.
Физический
маятник
—твёрдое тело, совершающее колебания
в поле каких-либо сил относительно
точки, не являющейся центром масс этого
тела, или неподвижной оси, перпендикулярной
направлению действия сил и не проходящей
через центр масс этого тела.![]()
Математи́ческий
ма́ятник —механическую
систему, состоящую из материальной
точки, находящейся на невесомой
нерастяжимой нити или на невесомом
стержне в однородном поле сил тяготения.
Период малых собственных колебаний
математического маятника длины L
неподвижно подвешенного в однородном
поле тяжести с ускорением свободного
падения g
равен
![]()
-
Затухающие колебания. Коэффициент затухания, время релаксации. Логарифмический декремент затухания.
Затуханием
колебаний
называется
постепенное ослабление колебаний с
течением времени, обусловленное потерей
энергии колебательной системой.
Бесконечно длящийся процесс вида
![]() в
природе невозможен.
Декрементом
затухания называется отношение амплитуды
затухающих колебаний в некоторый момент
времени t к амплитуде тех же колебаний
на период позже t + T: A(t)/A(t+T)=eβT
Декремент
затухания характеризует, во сколько
раз уменьшается амплитуда колебаний
за один период.
в
природе невозможен.
Декрементом
затухания называется отношение амплитуды
затухающих колебаний в некоторый момент
времени t к амплитуде тех же колебаний
на период позже t + T: A(t)/A(t+T)=eβT
Декремент
затухания характеризует, во сколько
раз уменьшается амплитуда колебаний
за один период.
Период
затухающих колебаний определяется
формулой:
![]() При
незначительном затухании период
колебаний практически равен
При
незначительном затухании период
колебаний практически равен![]() ….
….
![]() ---Такое отношение амплитуд называется
декрементом
затухания,
а его натуральный логарифм - логарифмическим
декрементом затухания:
---Такое отношение амплитуд называется
декрементом
затухания,
а его натуральный логарифм - логарифмическим
декрементом затухания:
![]()
Логарифмический
декремент затухания обратен по величине
числу колебаний, совершаемых за то
время, за которое амплитуда уменьшается
в «e» раз. Помимо рассмотренных величин
для характеристики колебательной
системы употребляется величина![]()
называемая добротностью колебательной системы. Добротность пропорциональна числу колебаний, совершаемых системой за то время, за которое амплитуда колебаний уменьшается в «e» раз.
время релаксации — время, за которое амплитуда колебаний уменьшится в e раз.
Добротность колебательной системы Q характеризует относительное изменение энергии за один период. Добротность пропорциональна отношению энергии W(t) системы в некоторый момент времени t к изменению энергии W(t) – W(t + t) за последующий период T. Q=2π (W(t)/W(t) – W(+T)) ///////
