Координатная форма векторного произведения.

ТЕОРЕМА 22.1. Пусть в пространстве выбран ортонормированный базис , в котором  и . Тогда

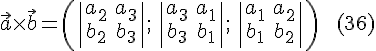
Доказательство. Рассмотрим ортонормированный базис , определяющий ориентацию пространства  и вычислим векторные произведения базисных векторов. Результаты занесем в таблицу

По определению координат вектора в базисе имеем

поэтому

Используя доказанные свойства векторного произведения, получаем

Используя результаты векторного произведения базисных векторов из таблицы, получим

Нетрудно видеть, что это подробная запись . Теорема доказана.

Приложения векторного произведения.

Вычисление площадей.

Задача 22.1. Пусть треугольник  задан координатами своих вершин  в декартовой системе координат. Найти площадь треугольника .

Решение. Из свойства 4. векторного произведения векторов получаем, что

Далее по формуле  находим

Наконец, используя формулы  и , окончательно получаем

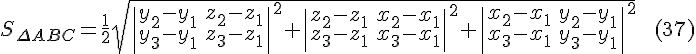
Если , то есть , то формула  приобретает вид:

23 Двойное векторное произведение.

Определение 23.1. Вектор  называется двойным векторным произведением.

Отметим, что векторы  и  компланарны. В самом деле это так, если векторы  и  коллинеарны. Если же векторы  и  не коллинеарны, то вектор им перпендикулярен, а вектор , перпендикулярный вектору , будет компланарен с векторами  и . Значит, если векторы  и неколлинеарны, то вектор  можно разложить по векторам  и .

Приводимая ниже формула и дает разложение этого вектора по векторам  и :

Для доказательства этой формулы введем ортонормированный базис, взяв первый единичный вектор  базиса коллинеарным вектору  и расположив второй единичный вектор  этого базиса перпендикулярно  и так, чтобы векторы  были компланарны. Тогда

По формуле  последовательно находим

С другой стороны, по формуле  имеем

поэтому

Нетрудно проверить, что и в случае коллинеарности векторов  и  формула  дает верный результат.

Отметим еще формулу

Действительно,

24 Смешанное произведение векторов.

Определение 24.1. Смешанным произведением векторов , взятых в указанном порядке, называется число, равное скалярному произведению вектора векторного произведения векторов  и  на вектор .

Обозначается смешанное произведение векторов  через . Используя данное обозначение, определение смешанного произведения кратко можно записать так:

Докажем теперь теорему, раскрывающую геометрический смысл смешанного произведения трех векторов в пространстве , ориентированном правой тройкой.

ТЕОРЕМА 24.1. Смешанное произведение некомпланарных векторов  численно равно объему параллелепипеда, построенного на этих векторах, как на ребрах, и взятого со знаком "", если тройка векторов  --- правая, и со знаком "", если тройка  --- левая. Смешанное произведение компланарных векторов равно нулю.

Доказательство. По определению смешанного произведения векторов имеем

Далее по определению скалярного произведения получаем, что

где  --- угол между векторами  и . Используя формулу , получаем , а по свойству 5. векторного произведения имеем . Поэтому

Заметим, что , где  --- высота параллелепипеда. Так как  --- правая, то:

1. если  --- правая, то  (см. рис. 1) и

2. если  --- левая, то  (см. рис. 2) и

3. если  --- компланарны, то, очевидно,  и

Свойства смешанного произведения.

1. При перестановке двух сомножителей смешанное произведение меняет знак. Циклическая перестановка не меняет знак смешанного произведения.

Доказательство. Действительно, из доказанной теоремы следует, что при любом порядке сомножителей смешанные произведения равны по абсолютной величине. С другой стороны, из определения ориентации пространства следует, что тройки векторов  определяют одну ориентацию пространства, а тройки векторов  другую. Поэтому имеем равенства

2. Скалярный множитель при любом аргументе можно выносить за знак смешанного произведения, т.е.

3. Смешанное произведение линейно относительно каждого аргумента, т.е.

Доказательство свойств 2. и 3. следует из аналогичных свойств векторного и скалярного произведений.

4. 

Доказательство. В самом деле, по доказанному свойству 1.

5. Для того чтобы смешанное произведение трех векторов равнялось нулю необходимо и достаточно, чтобы эти векторы были компланарны.

Доказательство. Нам нужно доказать только необходимость, поскольку достаточность доказана в теореме 24.1.

Пусть , тогда по определению получаем

Но это возможно только в случаях:

(a)  --- компланарны;

(b)  --- линейно зависимы, а значит, компланарны;

(c)  --- компланарны.

Координатная форма смешанного произведения.

ТЕОРЕМА 24.2. Пусть в пространстве выбран ортонормированный базис , в котором  и . Тогда

или

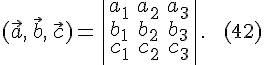
Доказательство. По определению смешанного произведения векторов имеем

По формуле  получаем

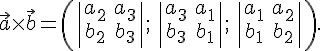
Используя формулу , приходим к формуле . Легко видеть, что правая часть формулы  есть разложение определителя третьего порядка, стоящего в правой части формулы  по элементам третьей строки. Теорема доказана.

Замечание 24.1. Если векторы  и  заданы относительно произвольного аффинного базиса , то формула  приобретает вид:

Следствие 24.1. Для того чтобы векторы  и , заданные относительно произвольного аффинного базиса  были компланарны необходимо и достаточно, чтобы

Приложения смешанного произведения.

Решим следующую задачу

Задача 24.1. Пусть три ребра тетраэдра (произвольная треугольная пирамида), выходящие из одной вершины совпадают с векторами . Найти объем этого тетраэдра.

Решение. Из школьного курса геометрии известно, что объемы параллелепипеда и пирамиды вычисляются по формулам

Поскольку основанием параллелепипеда является параллелограмм, а oснованием тетраэдра является треугольник, то площадь основания параллелепипеда в два раза больше площади основания тетраэдра. Поэтому получаем равенство

Из теоремы 24.1. следует, что , поэтому получаем, что