Взаимное расположение прямых и плоскостей в пространстве

1. Условие параллельности двух прямых.

Пусть даны две прямые

и

с направляющими векторами и соответственно. Параллельность двух прямых означает, очевидно, коллинеарность их направляющих векторов. Поэтому

.

2. Условие параллельности и перпендикулярности прямой и плоскости.

Если прямая

()

с направляющим вектором параллельна плоскости

()

с нормальным вектором , то, очевидно, и

.

Если , то , т.е.

.

3. Условие параллельности двух плоскостей.

Очевидно, плоскости и параллельны, если параллельны их нормальные векторы и :

.

Угол между двумя плоскостями.

Если коэффициенты плоскостей и не пропорциональны, то плоскости не параллельны, и, следовательно, пересекаются по некоторой прямой . Если взять любую точку на этой прямой и провести в каждой плоскости перпендикуляр к прямой в этой точке, то угол, образованный этими перпендикулярами, называется углом между плоскостями и . Понятно, что угол между нормальными векторами и равен углу между плоскостями и как углы с соответственно перпендикулярными сторонами. Тогда,

.

Угол между прямой и плоскостью.

Углом между прямой и плоскостью называется угол, образованный прямой и ее проекцией на эту плоскость. Если прямая задана каноническими уравнениями (29), а плоскость общим уравнением (22), то

или

.

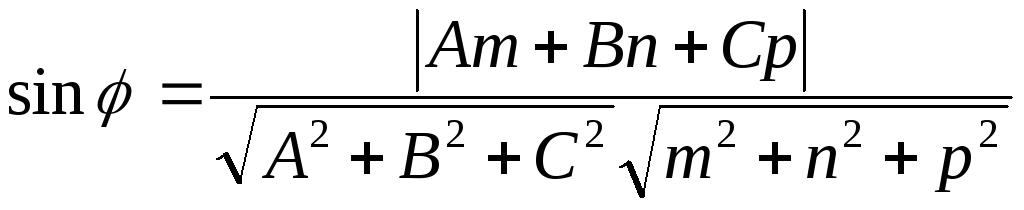Поверхности второго порядка

Поверхностью в называется множество точек , удовлетворяющих некоторому уравнению , называемому уравнением этой поверхности.

Говорят, что точка лежит на поверхности, если ее координаты удовлетворяют уравнению поверхности.

Среди множества поверхностей выделяют поверхности второго порядка, т.е. множества точек , координаты которых удовлетворяют уравнению вида:

,

где .

Оказывается, как и в случае с кривыми второго порядка, в пространстве всегда можно подобрать такую систему координат, в которой (1.5.10) принимает наиболее простой вид и задает:

1. Эллипсоид .

2. Однополосный гиперболоид .

3. Двуполостный гиперболоид .

4. Конус второго порядка . (1.5.14)

5. Эллиптический параболоид .

6. Гиперболический параболоид .

7. Точка .

8. Эллиптический цилиндр .

9. Гиперболический цилиндр .

10. Параболический цилиндр .

11. Пара пересекающихся плоскостей .

12. Пара параллельных или совпадающих плоскостей

13. Прямая .

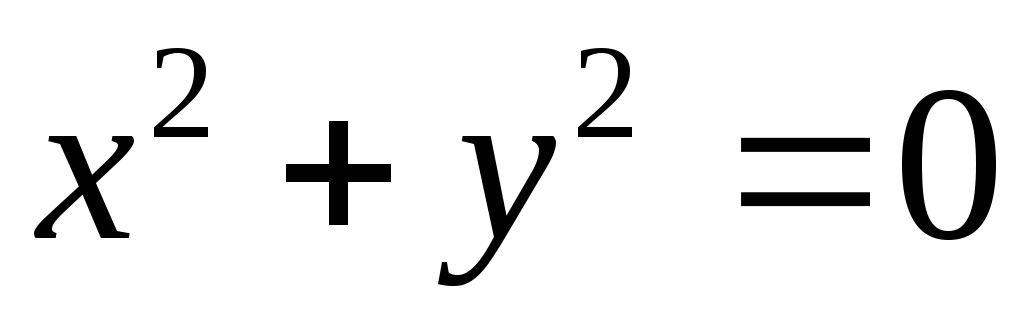Изучим некоторые характерные свойства вышеперечисленных поверхностей. Для определения их геометрического вида применим метод параллельных сечений.

1. Эллипсоид. Рассмотрим уравнение. Будем искать линии пересечения этой поверхности с плоскостями, параллельными плоскости , т.е. плоскостями . Получим:

– уравнения линий пересечения поверхности с плоскостью . Возможны следующие случаи:

1. , т.е. . Тогда – уравнение пустого множества точек, т.е. плоскость не пересекается с поверхностью.

2. , т.е. . Тогда , что возможно лишь при . Это значит, что плоскости касаются поверхности в точках и .

3. , т.е. . Тогда перепишем в виде

.

Это уравнения эллипсов. При получим:

– эллипс с максимальными полуосями и . Аналогично рассматриваются линии, получающиеся при сечении поверхности плоскостями и .

Полученные линии пересечения позволяют нам изобразить трехосный эллипсоид. При получим эллипсоид вращения вокруг оси . При получим сферу радиуса

2. Однополостный гиперболоид. Рассмотрим уравнение. Положим вначале , т.е.

или .

Это эллипсы. Полуоси будут наименьшими при . Если растет, то полуоси увеличиваются, и, соответственно, эллипсы увеличиваются. Теперь найдем линию пересечения с плоскостью при . Получим – гипербола. Если , то – гипербола. При всех остальных значениях или также получаются гиперболы.

Если в (1.5.12) знак “–“ расположен перед или перед , то, соответственно, однополостный гиперболоид содержит в себе либо ось , либо :

3. Двуполостный гиперболоид. Рассмотрим уравнение. В сечениях имеем .

1) Если , то получаем пустое множество.

2) Если , то получаем две точки и .

3) Если , то

. (1.5.27)

Это эллипсы, полуоси которых растут с ростом . При : - гипербола. При : - тоже гипербола.

4. Конус второго порядка. В уравнении при получаем эллипс . С ростом полуоси возрастают. В сечении плоскостями , имеем пары пересекающихся прямых и соответственно. В остальных случаях , – гиперболы.

5. Эллиптический параболоид. Возьмем в . Получим . Если , то получаем пустое множество. Если , то имеем одну точку . При получаем эллипсы, полуоси которых увеличиваются с ростом : . При из (1.5.15) получаем – уравнение параболы с осью симметрии и ветвями, направленными вверх. При получаем аналогично.

6. Гиперболический параболоид. Пересекая поверхность плоскостью получим: . При имеем пару пересекающихся прямых . При – гиперболы, , действительными осями, которых являются прямые, параллельные оси ; при – гиперболы, действительные оси которых параллельны оси . При имеем параболу , ось симметрии которой , ветви вверх и вершина в точке . При аналогично и ветви вниз. Это седлообразная поверхность изображена на рисунке:

7. Цилиндры второго порядка. Эллиптический цилиндр с уравнением на плоскости определяет эллипс, который называется направляющей линией цилиндра. Любая плоскость пересекает рассматриваемую поверхность по этому же эллипсу. Это значит, что если точка лежит на эллипсе, то и точка при любом лежит на поверхности эллиптического цилиндра. Прямые, параллельные оси и пересекающие направляющую линию (эллипс) называются образующими цилиндра.

Направляющими линиями гиперболического и параболического цилиндров с уравнениями (1.5.19) и (1.5.20) соответственно являются гипербола и парабола , а образующими служат прямые, параллельные оси и проходящие через указанную гиперболу и параболу.