16. Алгоритм построения многочлена Жегалкина

I. Алгоритм

1) Находим множество тех двоичных наборов, на которых функция принимает значение – 1.

2) Составляем СДНФ

3) В СДНФ каждый знак дизъюнкции заменяем на знак суммы Жегалкина

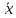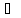4) Упрощаем, если можно, полученное выражение, используя тождество: _ix_i =1

5) В полученной формуле каждое отрицание заменяется на x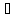1

6) Раскрываем скобки в полученной формуле, содержащей только функции конъюнкции, суммы по модулю 2, констант равных 1.

7) Приводим подобные используя тождество: x_i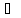x_i=0

II. С помощью неопределённых коэффициентов

Составляем систему линейных уравнений относительно 2ⁿ неизвестных коэффициентов содержащих 2ⁿ уравнений.

Решением системы являются коэффициенты a₀,a₁...a_n многочлена Жегалкина.

17. Функционально полные системы функции.

---

18. Принцип двойственности Теорем Поста и Шефферские функции.

1. Теорема Поста

Для того, что бы некоторый набор функций K был полным, необходимо и достаточно что бы в него входили функции не принадлежащие каждому из классов Т₀, Т₁, L, M, S.

Заметим, что необходимость этого утверждения очевидна, так как если бы все функции из набора К входили в один из перечисленных классов, то и все суперпозиции, а значит, и замыкание набора входило бы в этот класс и класс К не мог быть полным.

Достаточность этого утверждения доказывается довольно сложно, поэтому здесь не приводится.

Из этой теоремы следует довольно простой способ выяснения полноты некоторого набора функций. Для каждой из этих функций выясняется принадлежность к перечисленным выше классам. Результаты заносятся в так называемую таблицу Поста (в нашем примере эта таблица составлена для 4-х функций, причем знаком “+” отмечается принадлежность функции соответствующему классу, знак “–” означает, что функция в него не входит).

 

f	T0	T1	L	M	S
f1	+	–	+	–	–
f2	+	–	–	–	+
f3	–	+	–	–	–
f4	+	+	–	+	–

2. одним из способов проверки полноты какого-то набора К является проверка того, что через функции из этого набора выражаются функции другого полного набора (можно проверить, что через функции из К можно выразить конъюнкцию и отрицание или дизъюнкцию и отрицание.

Существуют такие функции, что одна такая функция сама является базисом (здесь достаточно проверить только полноту, неизбыточность очевидна). Такие функции называются шефферовскими функциями. Это название связано с тем, что штрих Шеффера является базисом.

Перейдем теперь к выяснению полноты конкретных наборов функций. Для этого перечислим 5 важнейших классов функций:

• Т₀ – это набор всех тех логических функций, которые на нулевом наборе принимают значение 0 (Т₀ – это класс функций, сохраняющих 0);

• Т₁ – это набор всех логических функций, которые на единичном наборе принимают значение 1 (Т₁ – это класс функций, сохраняющих единицу) (заметим, что число функций от п переменных принадлежащих классам Т₀ и Т₁ равно 2^2n-1);

• L – класс линейных функций т. е. функций, для которых полином Жегалкина содержит только первые степени переменных;

• М – класс монотонных функций. Опишем класс этих функций более подробно. Пусть имеются 2 набора из п переменных:x₁, x₂,..., x_n)

3. Для произвольных подмножеств A и B множества справедливы равенства

     (1)

Свойства, записанные равенствами (1), называются принципом двойственности. Их можно прочитать следующим образом: дополнение к объединению множеств равно пересечению их дополнений, а дополнение к пересечению множеств равно объединению их дополнений. Без труда принцип двойственности переносится на произвольное число подмножеств ; при этом записывают

     (2)

В этом случае символ дополнения C можно менять местами со знаком или , при этом знаки эти переходят один в другой.