
- •Интерполяция экспериментальных данных средствами mathcad
- •Кострома
- •Воронцова о.Р., Землякова и.В., Собашко ю.А. Интерполяция экспериментальных данных средствами MathCad: Учебно-методическое пособие. – Кострома: кгту, 2011. – 17 c.
- •Содержание
- •Введение
- •Основные понятия
- •Функции mathcad для линейной и сплайн-интерпрляции
- •3. Пример решения задания
- •4. Варианты заданий типового расчета
- •Вопросы для самопроверки
- •Рекомендуемая литература
Министерство образования и науки Российской федерации
Костромской государственный технологический университет
Кафедра высшей математики
Интерполяция экспериментальных данных средствами mathcad
Учебно-методическое пособие для студентов
специальности 230104, 230201, 230203
Кострома
2011
УДК
Воронцова о.Р., Землякова и.В., Собашко ю.А. Интерполяция экспериментальных данных средствами MathCad: Учебно-методическое пособие. – Кострома: кгту, 2011. – 17 c.
С Костромской государственный технологический университет
Содержание
Введение…………………………………………………………………… ……4
-
Основные понятия………………………………………………………..5
-
Функции MathCAD для линейной и сплайн-интерполяции………….9
-
Пример решения задания ………………………….……...…………….10
-
Варианты заданий для типового расчета………………………...……15
Вопросы для самопроверки…………………………………………………..17
Рекомендуемая литература……………………………………………………17
Введение
Миллионы людей занимаются математическими расчетами, иногда в силу влечения к таинствам математики и ее внутренней красоте, а чаще всего в силу профессиональной или иной необходимости. Ни одна серьезная разработка в любой отрасли науки и производства не обходится без трудоемких математических расчетов.
Вначале эти расчеты выполнялись на программируемых микрокалькуляторах или с помощью программ на универсальных языках программирования, таких как Паскаль. Постепенно для облегчения расчетов были созданы специальные математические компьютерные системы.
Системы MathCAD традиционно занимают особое место среди множества таких систем (Eureka, Mercury, MatLAB, Mathematica 2 и 3, Maple V R3 и R4 и др.) и по праву могут называться самыми современными, универсальными и массовыми математическими системами. Они позволяют выполнятькак численные, так и аналитические вычисления, имеют чрезвычайно удобный математико-ориентированный интерфейс и прекрасные средства графики.
Основная цель настоящего пособия – привить студентам практические навыки в использовании численных методов при решении прикладных задач с помощью одной из самых мощных и эффективных математических систем – MathCAD.
-
Основные понятия
В
прикладных применениях математики
часто приходится иметь дело с функциями
![]() ,
заданными лишь таблицей их значений.
,
заданными лишь таблицей их значений.
|
x |
x0 |
x1 |
... |
xn |
|
y |
y0 |
y1 |
... |
yn |
При
этом известно, что областью определения
![]() служит отрезок
служит отрезок
![]() ,
причем
,
причем
![]() .
.
Построение
достаточно простой для вычислений
функции
![]() ,
совпадающей в точках
,
совпадающей в точках
![]() со
значениями
со
значениями
![]() ,
а в остальных точках
,
а в остальных точках
![]() приближенно представляющей
приближенно представляющей
![]() с заданной точностью называется
интерполированием
функции.
с заданной точностью называется
интерполированием
функции.
Чаще
всего
![]() выбирают из класса полиномов (многочленов).
выбирают из класса полиномов (многочленов).
Итак,
требуется найти многочлен
![]() ,
значения которого в точках
,
значения которого в точках
![]() совпадают
со значениями функции
совпадают
со значениями функции
![]() ,
т. е.
,
т. е.
![]()
Многочлен
![]() называют интерполяционным
многочленом,
а точки
называют интерполяционным
многочленом,
а точки
![]() -
узлами
интерполяции.
-
узлами
интерполяции.
Интерполяционный многочлен, заданный в форме
 (1)
(1)
или
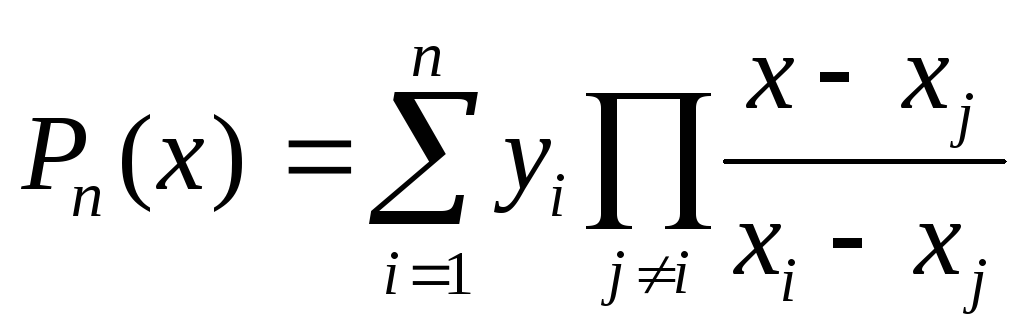
называют интерполяционным многочленом Лагранжа.
Частные случаи
-
Если
 для (1), то получаем случай линейного
интерполирования:
для (1), то получаем случай линейного
интерполирования: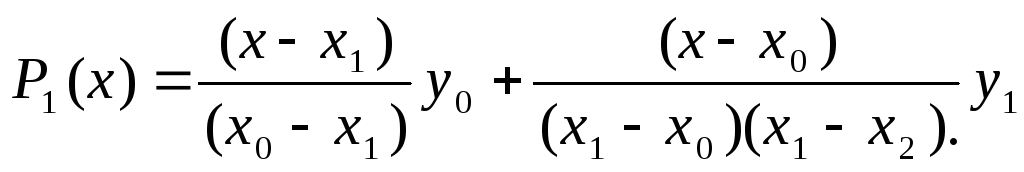 .
.
-
Если
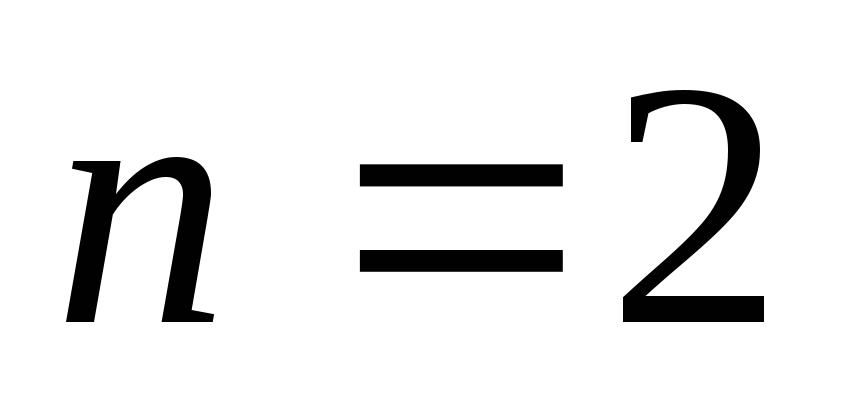 для (1), то получаем случай параболического
или квадратического интерполирования:
для (1), то получаем случай параболического
или квадратического интерполирования:

Если
узлы интерполяции
![]() равноотстоят друг от друга, то применяют
интерполяционный
многочлен Ньютона:
равноотстоят друг от друга, то применяют
интерполяционный
многочлен Ньютона:
![]() , (2)
, (2)
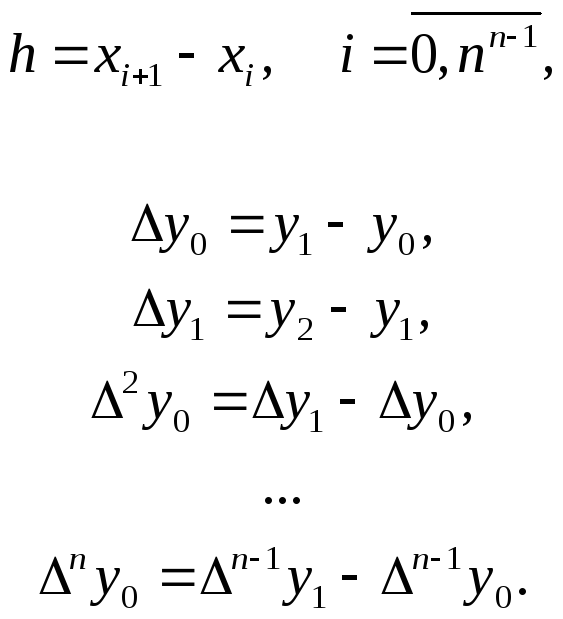
При
замене
![]() на
на
![]() полагаем, что
полагаем, что
![]() для
для
![]() и
и
![]() для
остальных
для
остальных
![]() .
.
![]() -
остаточный член интерполирования или
погрешность приближения функции
-
остаточный член интерполирования или
погрешность приближения функции
![]() интерполяционным многочленом
интерполяционным многочленом
![]() .
.
Пусть
![]() - (n+1)
раз дифференцируема на
- (n+1)
раз дифференцируема на
![]() .
Если
.
Если
![]() - интерполяционный многочлен Лагранжа,
то
- интерполяционный многочлен Лагранжа,
то
 (3)
для
(3)
для
![]() .
.
Если
![]() - интерполяционный многочлен Ньютона,
то
- интерполяционный многочлен Ньютона,
то
 . (4)
. (4)
Интерполирование
можно проводить между последовательными
точками
![]() ,
т.е. строить самостоятельные многочлены.
Совокупность
,
т.е. строить самостоятельные многочлены.
Совокупность
![]() формирует кусочно-полиномиалную кривую
формирует кусочно-полиномиалную кривую![]() .
.
Интерполирование
полиномом
![]() по (n+1)
тоже часто бывает неудовлетворительным.
Полином степени n
может иметь (n-1)
локальный максимум и минимум, и график
может раскачиваться, чтобы пройти через
точки.
по (n+1)
тоже часто бывает неудовлетворительным.
Полином степени n
может иметь (n-1)
локальный максимум и минимум, и график
может раскачиваться, чтобы пройти через
точки.
Разбиение отрезка на несколько частей с построением на каждой части самостоятельного интерполированного многочлена неудобно тем, что “на стыках” первая производная двух соседних интерполяционных многочленов может терпеть разрыв.
Поэтому
во многих задачах удобнее использовать
сплайны.
Разобьем
![]() на n
частей
точками
на n
частей
точками
![]() .
.
Сплайном
Sm(x)
называется
функция, определенная на
![]() и имеющая на нем непрерывную производную
(m-1)-го
порядка, которая на каждом частичном
отрезке
и имеющая на нем непрерывную производную
(m-1)-го
порядка, которая на каждом частичном
отрезке
![]() совпадает с некоторым многочленом
степени не выше m,
при этом хотя бы на одном из частичных
отрезков степень многочлена точно равна
m.
совпадает с некоторым многочленом
степени не выше m,
при этом хотя бы на одном из частичных
отрезков степень многочлена точно равна
m.
Сплайн,
принимающий в узлах
![]() те же значения
те же значения
![]() ,
что и некоторая функция
,
что и некоторая функция
![]() ,
называется интерполяционным.
,
называется интерполяционным.
На практике применяют кубические сплайны S3(x).
Разобьем
![]() на n
равных частичных отрезков длины
на n
равных частичных отрезков длины
![]() .
Тогда кубический сплайн на отрезке
.
Тогда кубический сплайн на отрезке
![]() ,
,
![]() запишется в виде:
запишется в виде:
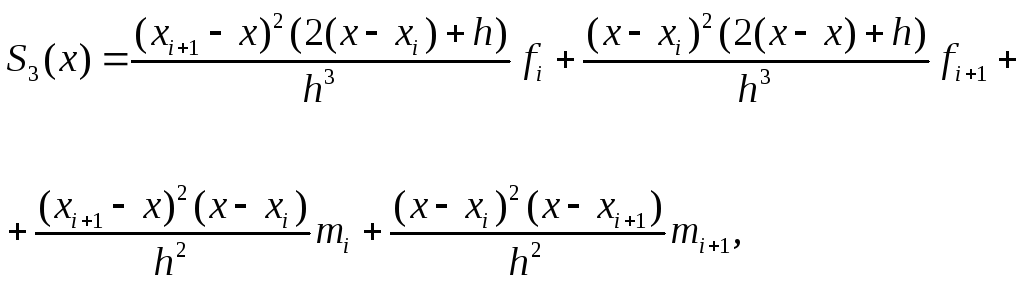
(5)
где
![]() -
некоторые числа. При этом
-
некоторые числа. При этом
![]()
![]() .
.
Выберем
величины
![]() так, чтобы была непрерывна и вторая
производная.
так, чтобы была непрерывна и вторая
производная.
Условия
непрерывности второй производной в т.
![]() ,
,
![]() .
.
![]()
Для
однозначного определения
![]() добавляют два условия, так называемые
краевые
условия.:
добавляют два условия, так называемые
краевые
условия.:
Например:
![]() ,
,
![]() .
.
Тогда

где
![]() .
.
