Текст лекции_8(14)

8

1. ОБЩИЕ ПОЛОЖЕНИЯ ОБ УСТОЙЧИВОСТИ САУ

При изложении методики составления структурных схем и дифференциальных уравнений систем автоматического управления отмечалось, что первым вопросом исследования систем является вопрос об их устойчивости. Этот вопрос важен, во-первых, потому, что в большинстве случаев неустойчивые системы непригодны для практического использования, и, во-вторых, потому, что даже в устойчивой системе необходимо знать, какие запасы устойчивости она имеет.

В результате анализа устойчивости обычно недостаточно получить прямой и однозначный ответ на вопрос, устойчива ли система; в большинстве практически встречающихся случаев разработчику системы нужно ясно представлять, какие из параметров элементов системы наиболее сильно влияют на устойчивость и как следует их изменить, чтобы обеспечить необходимые запасы устойчивости.

Ранее было показано, что устойчивая система после окончания переходного процесса переходит в новое вынужденное состояние; устойчивость системы может быть определена в результате решения уравнений для свободного движения системы: однородного дифференциального или характеристического уравнений системы.

Решение однородного дифференциального уравнения системы имеет вид

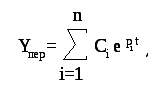(1)

где р_i — корни характеристического уравнения;

С_i — постоянные, определяемые из начальных условий.

Характеристическое уравнение n-гo порядка имеет n корней: p₁, p₂,…,.p_n. Эти корни могут быть действительными или комплексными попарно сопряженными.

Действительные корни дают в решении уравнения апериодическую составляющую вида

Очевидно, что если р_i<0, то это слагаемое с ростом t будет стремиться к нулю. Если же р_i≥0, то это слагаемое возрастает с ростом t и система будет неустойчивой. При р_i=0 это слагаемое становится равным C_i, т.е. общее решение системы, будет отличаться от частного решения на величину C_i.

Комплексные попарно сопряженные корни p_l=σ_l+jω_l и p_l=σ_l-jω_l соответствуют колебательным составляющим решения для свободного движения системы.

Если действительная часть комплексных сопряженных корней отрицательна (σ_l <0), то данная составляющая будет носить характер затухающих колебаний; если σ_l >0, то колебания будут нарастать, а при σ_l >0 они будут иметь постоянную амплитуду. Последние два случая (σ_l ≥0) приводят к неустойчивости системы.

Таким образом, система неустойчива, если хотя бы один из корней характеристического уравнения имеет положительную или равную нулю действительную часть. Следовательно, наиболее естественным методом определения устойчивости системы является решение ее характеристического уравнения и определение знаков действительных частей полученных корней. Однако такой метод хотя и позволяет получить ответ на вопрос об устойчивости системы, не может считаться приемлемым для большинства практических задач.

Это связано с математическими трудностями, возникающими при решении алгебраических уравнений высоких степеней. Поэтому на практике применяются другие методы, позволяющие, не прибегая к решению дифференциального или характеристического уравнения, а иногда даже и к составлению этих уравнений, получить все необходимые данные по устойчивости. Такие методы называются критериями устойчивости. Следует отметить, что все критерии устойчивости в той или иной форме используют тот факт, что у устойчивой системы действительные части всех корней характеристического уравнения отрицательны, однако знак действительных частей корней характеристического уравнения устанавливается не непосредственно в результате их определения, а косвенным путем.

2. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ

Наиболее наглядными с этой точки зрения являются алгебраические критерии, предложенные Раусом (1875 г.) и Гурвицем (1895 г.). Так как эти критерии отличаются только деталями, ограничимся изложением критерия Гурвица. Гурвиц, формулируя свой критерий, ставил перед собой чисто математическую задачу: найти сравнительно простой метод, позволяющий определить, не имеет ли один из корней алгебраического уравнения положительную (или равную нулю) действительную часть. Как известно, если в качестве такого уравнения взять характеристическое уравнение системы, то ответ на этот вопрос позволит определить, устойчива ли данная система.

Для применения критерия Гурвица строится специальный определитель из коэффициентов характеристического уравнения. Для уравнения шестого порядка, например, определитель Гурвица имеет вид

a5	a6	0	0	0	0
a3	a4	a5	a6	0	0
a1	a2	a3	a4	a5	a6
0	a0	a1	a2	a3	a4
0	0	0	a0	a1	a2
0	0	0	0	0	a0

Метод построения определителя состоит в том, что в правом нижнем углу записывается коэффициент a₀, а дальше по большой диагонали снизу — вверх — все коэффициенты по порядку: a₁, a₂, a₃,…a₅,.Основываясь на полученной таким образом большой диагонали, можно заполнить все остальные участки определителя; при этом справа от большой диагонали записываются по порядку коэффициенты с возрастающими номерами, слева — с убывающими. Если какой-либо из коэффициентов отсутствует, то на его место ставится 0. Например, слева от a₀ и справа от a_n всегда будут нули (n — порядок характеристического уравнения). Определитель может быть построен и другим методом; в левом верхнем углу записывается коэффициент a_n-1 , а справа от него по верхней строке определителя — все остальные коэффициенты с возрастающими номерами: a_n , 0, ..., 0. Вторая строка начинается с a_n-3, и справа опять записываются коэффициенты с возрастающими номерами: a_n-2, a_n-1, a_n, 0,…,0. Все следующие строки определителя начинаются с последующих коэффициентов с нечетными номерами: a_n-5, a_n-7,…, справа от которых идут коэффициенты с возрастающими номерами. Так же как и в первом методе составления определителя, все отсутствующие коэффициенты заменяются нулями. Так как оба метода составления определителя дают одинаковый результат, можно, составляя определитель Гурвица с помощью одного из них, применить другой для проверки.

Анализируемое уравнение не будет иметь корней с положительной действительной частью, т. е. система, которой это уравнение соответствует, будет устойчива, если коэффициент a_n>0 и в определителе Гурвица миноры Δ₁, Δ₂, … Δ_n будут положительными. Если в исходном характеристическом уравнении коэффициент a_n<0 , то, умножив все уравнение на -1, можно обеспечить выполнение условия a_n>0.

Миноры Гурвица являются частями определителя, например:

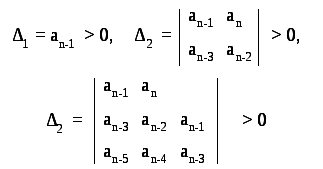
и т. д. Очевидно, что для уравнения n-го порядка Δ_n = a₀ Δ_n-1 (так как все остальные члены в нижней строке равны 0).

Следовательно, для проверки устойчивости системы достаточно найти миноры от Δ₁ до Δ_n-1.

Если один из миноров меньше нуля, то по меньшей мере один из корней будет иметь положительную действительную часть, а значит, система, которой соответствует это характеристическое уравнение, будет неустойчивой.

Так как при анализе устойчивости необходимо не только ответить на вопрос о том, устойчива ли система, но и определить, в каких пределах могут изменяться отдельные параметры элементов системы и как они влияют на устойчивость, то очевидно, что критерий Гурвица не позволяет получить полный ответ на этот вопрос. Действительно, изменение любого параметра системы приводит к новому характеристическому уравнению, а следовательно, нужно заново применять критерий Гурвица. Исключение составляют только самые простые системы, которые имеют характеристические уравнения второго и третьего порядков. Так как такие простые случаи сравнительно редко встречаются на практике, то и критерий Гурвица в последние годы применяется все реже.

Таким образом, применение критерия Гурвица к реальным системам приводит к сложным вычислениям, а главное, не позволяет выявлять влияние отдельных параметров элементов на работу системы в целом. Если, например, в результате анализа выяснилось, что система неустойчива, то критерий Гурвица не дает указаний, какой из параметров элементов системы и на какую величину должен быть изменен, чтобы сделать систему устойчивой. В более сложных случаях, когда необходимо обеспечить определенные параметры переходного процесса, критерий Гурвица не дает никаких сведений о влиянии параметров элементов системы на вид переходного процесса. Все эти недостатки, свойственные алгебраическим критериям (Рауса и Гурвица), естественно, ограничивают их применение.

3. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ

Развитие теории автоматического управления привело к созданию новых методов анализа САУ. В этом отношении наиболее плодотворными оказались методы, ранее использовавшиеся в радиотехнике (в частности, при анализе работы усилителей с отрицательной обратной связью), так называемые частотные методы.

Наиболее важное открытие в этой области было сделано советским ученым А. В. Михайловым, который в 1938 г. впервые предложил применить частотные методы для анализа устойчивости систем автоматического управления. А. В. Михайлов создал критерий устойчивости (называемый его именем), основанный на рассмотрении поведения замкнутой системы при подаче на ее вход гармонического колебания с частотой, изменяющейся от нуля до бесконечности. Критерий устойчивости Михайлова позволяет оценить устойчивость замкнутой системы по характеристическому уравнению замкнутой системы.

По существу критерий Михайлова также основан на определении знаков корней характеристического уравнения системы, но при этом нет необходимости в определении значений корней, т. е. в решении характеристического уравнения.

Помимо критерия Михайлова, применяющегося для анализа замкнутых систем автоматического управления, возможен и другой метод выяснения устойчивости системы, когда об устойчивости замкнутой системы судят по амплитудно-фазовой или частотным характеристикам разомкнутой системы. Этот метод, называемый критерием Найквиста, получил в настоящее время наиболее широкое распространение благодаря его простоте, богатству физического содержания, наглядности результатов, легкости постановки эксперимента для проверки расчетов или получения недостающих сведений и отсутствию сложных вычислений.

Критерий Найквиста позволяет связать стационарные частотные свойства разомкнутой системы с нестационарными свойствами замкнутой системы.

Для исследования замкнутой системы на устойчивость при применении критерия Найквиста эту систему разрывают в какой-либо точке соединения двух звеньев. При этом замкнутая система превращается в разомкнутую. Точка разрыва должна обладать свойством детектирования, т. е. в этом месте не должно быть реакции последующего звена на предыдущее.

На образованный в точке разрыва вход системы подается колебание постоянной амплитуды x и частоты ω. Пройдя через систему, это колебание появится на выходе системы в виде колебаний той же частоты, но с амплитудой и фазой, отличающимися от тех же параметров входного колебания.

Критерий устойчивости Найквиста формулируется следующим образом: если в системе, устойчивой в разомкнутом состоянии, годограф амплитудно-фазовой характеристики не охватывает точку с координатами (-1, j0), то эта систем а будет устойчивой и в замкнутом состоянии (кривая 1 на рис. 5.5); если же годограф охватывает эту точку, то в замкнутом состоянии система будет неустойчивой (кривая 2).

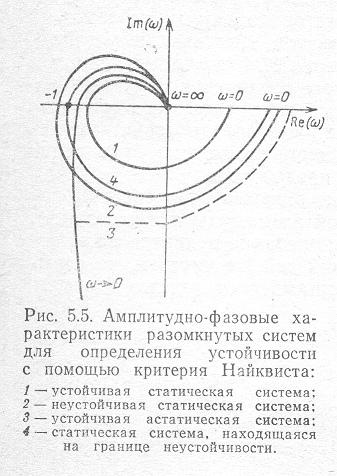
Выражение «охватывает» можно пояснить следующим образом: если из точки с координатами (-1, j0) построить вектор ко всем точкам амплитудно-фазовой характеристики, то при изменении частоты от 0 до ∞ у устойчивой системы суммарный поворот этого вектора будет равен 0, а у неустойчивой -2π. При этом в астатических системах для определения суммарного угла поворота этого вектора необходимо дополнить годограф амплитудно-фазовой характеристики дугой бесконечно большого радиуса, соединяющей точку годографа при ω→0 с действительной осью (кривая 3).

Об устойчивости можно также судить по амплитудно-частотным и фазо-частотным характеристикам. При этом у системы, устойчивой в разомкнутом и замкнутом состояниях, на частоте ω_ср при которой амплитудно-частотная характеристика проходит через уровень 1, фазо-частотная характеристика не должна достигать уровня –π; или, что то же самое, при частоте ω_кр, на которой фазо-частотная характеристика проходит через уровень –π, амплитудно-частотная характеристика должна иметь значение меньше 1.

Амплитудно-фазовая характеристика может быть определена как расчетным (по амплитудно-фазовым характеристикам отдельных звеньев), так и экспериментальным путем. В последнем случае производится измерение амплитуды и фазы входного и выходного колебаний при различных частотах и строятся частотные или амплитудно-фазовые характеристики. Эти два метода (расчетный и экспериментальный) определения амплитудно-фазовой характеристики могут сочетаться, т. е. могут рассчитываться характеристики некоторых звеньев и экспериментально определяться характеристики других звеньев. Возможность такого сочетания является большим достоинством этого метода анализа систем автоматического управления.

Если амплитудно-фазовая характеристика проходит через точку с координатами (-1, j0), то система будет находиться на границе неустойчивости; следовательно, граница неустойчивости имеет место при совпадении частоты среза системы с критической частотой. Граница неустойчивости означает наличие незатухающих гармонических колебаний в системе при отсутствии входного сигнала; это полностью соответствует известному из курса «Радиотехнические цепи и сигналы» условию возникновения колебаний в случае, если в замкнутой системе имеет место равенство фаз и амплитуд входного и выходного колебаний (кривая 4, на рис. 5.5)

Действительно, после прохождения сигнала через систему, находящуюся на границе неустойчивости, выходной сигнал будет иметь такую же амплитуду, как и входной сигнал, и фазу, отличающуюся на –π. Так как при замыкании системы выходной сигнал подается на вход в противофазе, т. е. дополнительно поворачивается на –π, то в этом случае будет иметь место равенство фаз и амплитуд, что создает условия для возникновения колебаний.

Поясним физический смысл рассматриваемого критерия устойчивости. Рассмотрим замкнутую систему, в которой под влиянием какого-то внешнего воздействия возникли затухающие колебания. Будем изменять один из параметров системы (наиболее наглядным является изменение коэффициента усиления) в такую сторону, чтобы в системе уменьшалось затухание; тогда при каком-то значении этого параметра система станет неустойчивой, т. е. в ней воз- никнут незатухающие колебания с некоторой частотой ω_кр. Сохранив последнее значение изменяемого параметра системы, разорвем ее в какой-то точке и подадим на вход колебание, имеющее частоту ω_кр. При этом модуль амплитудно-фазовой характеристики будет равен 1, а аргумент 0, так как иначе замкнутая система не могла бы поддерживать незатухающие колебания с дан- ной частотой. Если еще больше изменить данный параметр, что приведет к дальнейшему уменьшению устойчивости, то при частоте, которой соответствует φ(ω)=0, модуль амплитудно-фазовой характеристики будет больше 1. Это означает, что сигнал после каждого прохода по разомкнутой системе будет возвращаться усиленным, т. е. амплитуда колебаний в замкнутой системе будет нарастать.

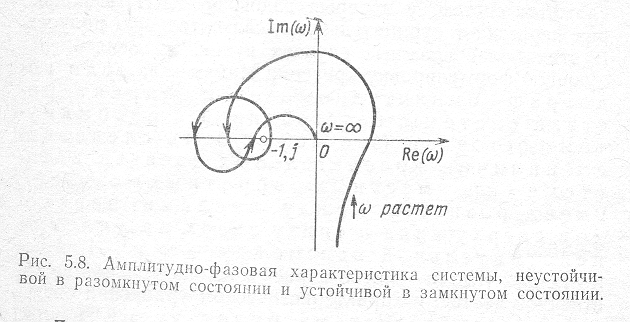
В более сложных случаях при анализе сложных систем, у которых годограф ККП несколько раз пересекает отрицательную действительную полуось, необходимо применять следующую формулировку критерия Найквиста: Если годограф амплитудно-фазовой характеристоки системы, неустойчивой в разомкнутом состоянии (это может быть следствием наличия колебательных звеньев в системе или местных обратных связей) имеет разность между числами переходов сверху вниз и снизу вверх на участке действительной оси между -∞ и -1, paвную т /2 (где т — число корней с положительной вещественной частью в характеристическом уравнении системы), то такая система будет устойчивой. В частном случае, когда все корни характеристического уравнения имеют отрицательную вещественную часть (m=0), соответственно в устойчивой системе число переходов этого участка действительной оси равно нулю.

На рис. 5.8 дан годограф ККП системы, неустойчивой в разомкнутом состоянии и устойчивой в замкнутом состоянии, характеристическое уравнение которой имеет два корня с положительной вещественной частью.

Ранее неоднократно отмечались преимущества метода логарифмических характеристик, особенно для сложных систем. Это в равной мере относится и к анализу устойчивости. Для простых систем, устойчивых в разомкнутом состоянии, анализ устойчивости по логарифмическим характеристикам полностью аналогичен анализу устойчивости по обычным амплитудно- и фазо-частотным характеристикам. Таким образом, если в системе ω_ср<ω_кра, то она устойчива; если ω_ср=ω_кр, то система находится на границе неустойчивости; и, наконец, если ω_ср>ω_кр, то система неустойчива.

Запасы устойчивости определяются по логарифмическим частотным характеристикам таким же способом, как и по обычным частотным характеристикам. Следует только учитывать, что запас устойчивости по амплитуде (усилению) ΔА будет выражен в децибелах. Обычно считаются приемлемыми запасы устойчивости ΔА =10…20 дб и Δφ= 30…40 градусов.