IV. Поверхностные интегралы. Элементы теории поля

§1. Поверхностные интегралы первого рода

Поверхностные интегралы первого рода представляют собой такое же естественное обобщение двойных интегралов, каким криволинейные интегралы первого рода являются по отношению к определенным интегралам.

Пусть в точках некоторой поверхности (S), гладкой или кусочно-гладкой определена ограниченная функция f(M)=f(x;y;z). Разобьем поверхность (S) на n произвольных частей с площадями S₁, S₂, …, S_n и диаметрами λ_i. Обозначим -диаметр разбиения. Выбрав на каждой частичной поверхности произвольную точку , составим сумму:

.

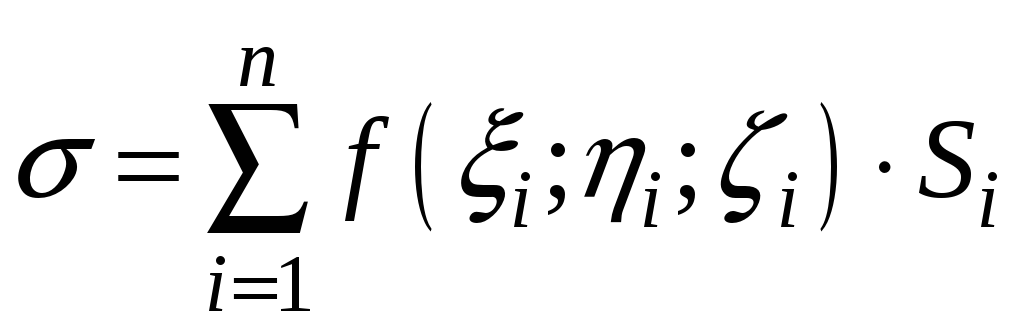Данная сумма называется интегральной суммой для функции f(M) по поверхности (S).

Определение. Если существует конечный предел I при 0 интегральной суммы , не зависящий ни от способа разбиения поверхности (S), ни от выбора промежуточных точек M_i, то он называется поверхностным интегралом первого рода от функции f(x;y;z) по поверхности (S).

Обозначается или .

Таким образом, .

Если f(x;y;z)1 на поверхности (S), то . То есть поверхностный интеграл первого рода по поверхности (S) выражает площадь этой поверхности.

Вычисление поверхностного интеграла первого рода производится сведением поверхностного интеграла к двойному.

Теорема. Пусть поверхность (S) задана уравнением z=z(x;y), где функция f(x;y) вместе с производными и непрерывна в замкнутой области (G) – проекции (S) на плоскость Оху. Пусть функция f(x;y;z) непрерывна на поверхности (S). Тогда существует поверхностный интеграл первого рода по этой поверхности и он сводится к двойному интегралу следующим образом:

.

Доказательство.

Разобьем поверхность (S) произвольно на n частей и спроецируем это разбиение на плоскость Оху. Получим соответственно разбиение области (G) на части (G₁), (G₂), …, (G_n). Пусть  - диаметр разбиения. В каждой части (G_i) выберем произвольно точку . На поверхности (S) ей соответствует точка , где . Составим интегральную сумму для поверхностного интеграла первого рода: .

К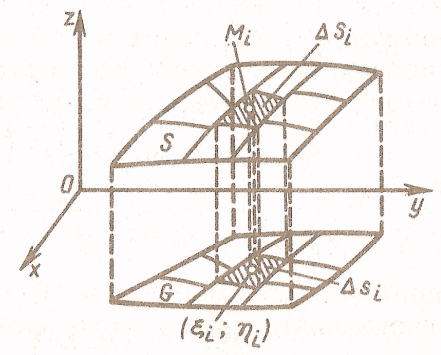ак было показано при выводе формулы площади поверхности

.

Тогда

. (1)

В правой части равенства (1) стоит интегральная сумма для интеграла

.

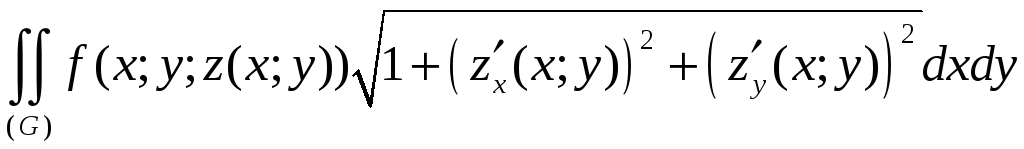Функция в силу условий теоремы непрерывна на области (G), а следовательно, интегрируема на ней.

Переходя в равенстве (1) к пределу при 0 получаем искомую формулу.

Свойства двойных интегралов и условия их существования без особых изменений переносятся на поверхностные интегралы.

Физический смысл поверхностного интеграла первого рода. Если на поверхности (S) распределена масса, плотность которой в каждой точке М(x;y;z)(S), равна f(x;y;z) то интеграл , т. е. представляет собой всю массу, распределенную по поверхности.

Пример. В каждой точке поверхности (S), лежащей в первом октанте, уравнение которой x+y+z=1 , распределена масса с плотностью , где k=const. Вычислить эту массу.

 z=1-x-y, , . Тогда

. 

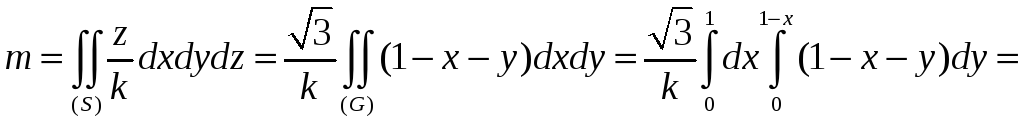
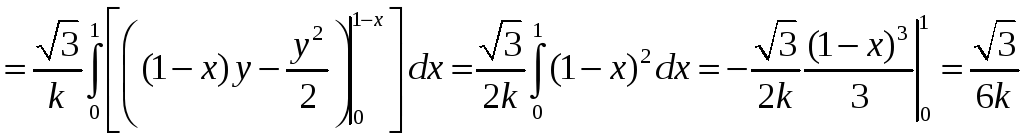§2. Двусторонние и односторонние поверхности. Сторона поверхности

Рассмотрим некоторую поверхность (S) и нормаль в точке М к поверхности. Зафиксируем на нормали одно из двух возможных направлений. Через точку М проведем замкнутый контур, не имеющий общих точек с границей поверхности. Если мы будем перемещать основание нормали в направлении MAM₁BM, то нормаль, обойдя этот контур, вернется к точке М и займет либо исходное положение , либо перевернутое . Если на поверхности нет ни одного контура, который переворачивал бы нормаль после его обхода, то такая поверхность называется двусторонней, а если есть хотя бы один контур, переворачивающий нормаль, то такая поверхность называется односторонней.

Примером односторонней поверхности может служить лист Мёбиуса. Его модель можно получить, если прямоугольный кусок бумаги ABCD, перекрутив один раз, склеить, соединив точку А с точкой С, а точку В с точкой D. Если полученное перекрученное кольцо начать красить в какой-либо цвет, то можно, не переходя через его границы, покрасить все кольцо этим цветом. В дальнейшем подобные поверхности рассматривать не будем.

Определение. Совокупность точек двусторонней поверхности с соответствующими направлениями нормалей, непрерывно переходящих друг в друга при перемещении основания нормали по поверхности, не пересекая его границы, называется стороной поверхности.

Выберем определенную сторону незамкнутой двусторонней поверхности, а в ней замкнутый контур Г. Он ориентирован положительно, если обход совершается против часовой стрелки, и ориентирован отрицательно, если обходится по часовой стрелке.

Построим в точке поверхности, лежащей внутри контура, нормаль к поверхности и воспользуемся: «правилом буравчика».

Поверхность является положительно ориентированной, если при обходе контура Г в положительном направлении движение винта совпадает с направлением нормали. Если движение винта противоположно направлению нормали, то поверхность отрицательно ориентирована.

Для замкнутой поверхности считается, что внешняя поверхность ориентирована положительно, а внутренняя - отрицательно.