
- •24. Конструкция и принцип работы многоэмиттерного транзистора.
- •25. Закон Мура. Степень интеграции интегральных схем.
- •26. Диод Шоттки. Принцип работы. Технология изготовления.
- •27. Вертикальная структура транзистора Шоттки.
- •28. Работа биполярного транзистора в ключевом режиме
- •29. 0Сновные схемы включения биполярного транзистора.
- •30. .Конструкция конденсатора в интегральном исполнении.
- •31. Структура интегрального резистора
- •32. 3Акон Мура. Степень интеграции интегральных микросхем.
- •33. 3Акон Мура…
24. Конструкция и принцип работы многоэмиттерного транзистора.
Многоэмиттерный транзистор (МЭТ) это биполярный транзистор, который имеет несколько эмиттерных областей. Различают МЭТ в которых эмиттерные области объединены одним внешним выводом, и МЭТ в которых каждая эмиттерная область имеет отдельный внешний вывод.
МЭТ, эмиттерные области которых объединены одним внешним выводом, характеризуются большим значением отношения периметра эмиттера к его площади, что обеспечивает уменьшение сопротивления базы транзистора и увеличение плотности его эмиттерного тока. Такие транзисторы применяют главным образом в качестве мощных ВЧ и СВЧ транзисторов. Наиболее распространёнными являются МЭТ с полосковой, ячеистой и сетчатой формами эмиттерной области. МЭТ с ячеистой формой эмиттерной области имеют наибольшую (по сравнению с другими МЭТ) величину отношения периметра эмиттера к его площади, что обеспечивает максимальное усиление по мощности. МЭТ с сетчатой формой эмиттерной области имеют наибольшее (по сравнению с другими МЭТ) значение отношения суммарной площади эмиттерных областей к площади коллекторной области, что обеспечивает работу такого транзистора при значительных рабочих токах.
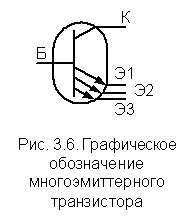
МЭТ, в которых каждая эмиттерная область имеет отдельный внешний вывод (рис. 3.6), используются в транзисторно-транзисторной логике в качестве логического элемента «И». Отличительной особенностью таких транзисторов является достаточно большое расстояние между отдельными эмиттерными областями и наличие сопротивления между базовой областью и её внешним выводом, что обеспечивает уменьшение коэффициента передачи тока между эмиттерными областями, а также малую величину инверсного коэффициента передачи тока и соответственно увеличение нагрузочной способности транзистора. Увеличение скорости переключения таких МЭТ достигается уменьшением площади эмиттерных областей.
25. Закон Мура. Степень интеграции интегральных схем.
Зако́н Му́ра — эмпирическое наблюдение, сделанное в 1965 году (через шесть лет после изобретения интегральной схемы), в процессе подготовки выступления Гордоном Муром (одним из основателей Intel).
Мур высказал предположение, что число транзисторов на кристалле будет удваиваться каждые 24 месяца. При анализе графика роста производительности запоминающих микросхем им была обнаружена закономерность: появление новых моделей микросхем наблюдалось спустя примерно одинаковые периоды (18—24 мес.) после предшественников, при этом количество транзисторов в них возрастало каждый раз приблизительно вдвое. Гордон Мур пришел к выводу, что при сохранении этой тенденции мощность вычислительных устройств за относительно короткий промежуток времени может вырасти экспоненциально.
Это наблюдение получило название закон Мура. Существует масса схожих утверждений, которые характеризуют процессы экспоненциального роста, также именуемых «законами Мура». К примеру, менее известный «второй закон Мура»[1], введённый в 1998 году Юджином Мейераном, который гласит, что стоимость фабрик по производству микросхем экспоненциально возрастает с усложнением производимых микросхем. Так, стоимость фабрики, на которой корпорация Intel производила микросхемы динамической памяти ёмкостью 1 Кбит, составляла 4 млн. $, а оборудование по производству микропроцессора Pentium по 0,6-микрометровой технологии c 5,5 млн. транзисторов обошлось в 2 млрд. $. Стоимость же Fab32, завода по производству процессоров на базе 45-нм техпроцесса, составила 3 млрд. $[2].
В 2007 году Мур заявил, что закон, очевидно, скоро перестанет действовать из-за атомарной природы вещества и ограничения скорости света
Одним из физических ограничений на миниатюризацию электронных схем является также Принцип Ландауэра, согласно которому логические схемы, не являющиеся обратимыми, должны выделять теплоту в количестве, пропорциональном количеству стираемых (безвозвратно потерянных) данных. Возможности по отводу теплоты физически ограничены
Параллелизм и закон Мура
В последнее время, чтобы получить возможность задействовать на практике ту дополнительную вычислительную мощность, которую предсказывает закон Мура, стало необходимо задействовать параллельные вычисления. На протяжении многих лет, производители процессоров постоянно увеличивали тактовую частоту и параллелизм на уровне инструкций, так что на новых процессорах старые однопоточные приложения исполнялись быстрее без каких либо изменений в программном коде. Сейчас по разным причинам производители процессоров предпочитают многоядерные архитектуры, и для получения всей выгоды от возросшей производительности ЦП программы должны переписываться в соответствующей манере. Однако, по фундаментальным причинам, это возможно не всегда.
ИНТЕГРАЦИИ СТЕПЕНЬ
(К) - показатель, характеризующий сложность интегральной схемы', численно определяется выражением К = IgN, где N - число элементов, входящих в ИС (значение К округляется до ближайшего целого числа в сторону увеличения). Однако чаше пользуются другой оценкой сложности И. с., в соответствии с к-рой различают малые N < 102), средние (N = 102 - 103), большие (N = 103 - 104) и сверхбольшие W = 104) интегральные схемы.
