1.6. Граничные условия. Наибольшие напряжения и прогибы.

      Условия прочности

Так как число произвольных постоянных в уравнении (4.41) равно трем, то для нахождения постоянных С следует составить следующие три граничные условия:

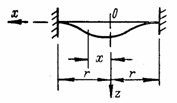
 для защемленной кромки пла­стины (рис. 28,а) 1) х = r,  w = 0;    2) x = r,   = 0;   3) x = 0,   = 0;	а
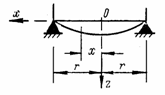
 для свободно опертой кромки пластины (рис. 28, б) 1) х = r,  w = 0;    2) x = r,  Mr = 0;   3) x = 0,   = 0;	б
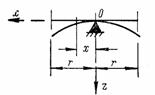
 для свободной кромки (рис. 28,в) 1) х = r,  Mr = 0;    2) x = r,  ;   3) x = 0,    w = 0.	в
	Рис. 28

 

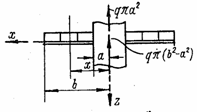
Дифференциальное уравнение (4.38) и его интегралы, а также выражения (4.31) справедливы и для кольцевой пластины в виде круг­лой пластины с круглым  отверстием  в  середине  (рис. 68,а)  или  в  виде  кольцевой пластины,

а	б	в

Рис. 29

 

внутренний контур которой защемлен (рис. 29,б). Изменяются лишь граничные условия и для центральной силы Р должно быть составлено вы­ражение, отражающее изменение поперечной силы в сечении х [см. формулу (4.37)].

 Например, для пластины, изображенной на рис. 29, а, граничное условие    х = 0, w = 0 теряет смысл, так как при х = 0 нет пластины. Поэтому следует воспользоваться следующими тремя условиями: 1) х = b; w = 0; 2) х =b,  = 0; 3) x = a, M_r = 0. Для сосредоточенной силы получится выраже­ние

.

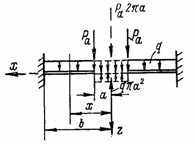
В этом выражении первый член представляет собой приложен­ную в центре и направленную вниз равнодействующую погонных сил P_a, приложенных к контуру ра­диусом а (сила Р на рис. 26), а второй член  силу, приложенную в центре и направленную вверх, ком­пенсирующую ту распределенную на­грузку, которой надо заполнить круг радиусом а, чтобы привести схему, изображенную на рис, к схе­ме, показанной на рис. 29,а. При такой замене уравнения остаются в силе и при наличии отверстия, так как коорди­наты х всегда больше а и изменение расчетной схемы при х < а на вывод этих уравнений не влияет.

Для пластины, изображенной на рис. 29,б, следует воспользоваться следующими граничными условиями:

1)          х = а, w = 0; 2) х = а,  = 0; 3) х = b, M_r = 0. Для сосредото­ченной силы получится выражение

       .

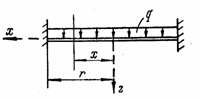
Если, в частном случае, одна из нагрузок q или Р отсутствует, то в формулах (4.40) и (4.41) ее следует положить равной нулю. Например, для пластины, показанной на рис. 29,в, вы­ражение для прогиба будет

.

Если для отдельных участков пластины выражения попереч­ной силы различны (рис. 30), то для каждого из участков  должно   быть  составлено  свое дифференциальное уравнение. Например, для суммарной поперечной силы на первом участке пластины

,

на втором участке

.

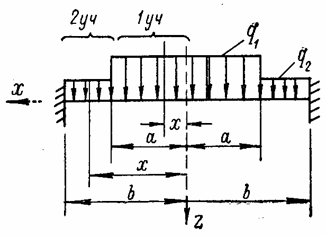
Рис. 30

 

После интегрирования каждого дифференциального уравнения получится три произвольных постоянных и общее число произ­вольных постоянных окажется равным 3п (п  число участков). Для каждой границы между двумя соседними участками могут быть составлены три дополнительных условия, выражающих то обстоятельство, что на границе двух соседних участков прогиб w, угол  и радиальный момент М_r одинаковы: 1) х = a, w₁ =w₂, 2) х = a, ; 3) х = а, (М_r)₁= (М_r)₂. Таких дополнитель­ных условий оказывается как раз столько, сколько недостает для нахождения всех произвольных постоянных. В разобранном при­мере при двух участках число произвольных постоянных 2  3 = 6, число условий 3 + 3 = 6.

Если известны выражения для изгибающих моментов  М_r  и  М_T  и прогибов w в функции от х, то координаты х, соответствующие наибольшим значениям этих вели­чин, найдутся из условий

.                              (4.42)

В ряде случаев сечения, в ко­торых возникают наибольшие из­гибающие моменты или прогибы, известны. Например, в схеме на рис. 68,б наибольший прогиб возникает на наружном контуре при х = b, а наибольший радиальный изгибающий момент (M_r)_max  в защемлении при х = а.

Подставив найденные из условий (4.42) значения х в выражения для изгибающих моментов, можно получить значения (M_r)_max и (М_Т)_max которые, в общем случае, могут возникнуть в разных сечениях пластины. Опасное сечение может оказаться поэтому там, где погонные изгибающие моменты М_r и M_T одно­временно велики.

Главные напряжения на наружной и внутренней поверхностях пластины в опасном сечении вычисляются по формулам, анало­гичным (4.27), путем замены момента инерции на момент сопротивления:

 .

Третье главное напряжение (по площадке, параллельной сре­динной плоскости) равно нулю. Расчетное напряжение, сравнивае­мое с допускаемым, вычисляется в зависимости от знаков напря­жений и  по одной из теорий прочности. Например, для пластины, представленной на рис. 68,б, опасное сечение находится в защемлении при х = а; при этом верхние волокна и от момента М_r, и от момента М_T испытывают растяже­ние, а нижние  сжатие, изгибающий момент М_r в сечении х = а больше, чем М_T. Предполагаем, что пластина выполнена из пла­стического материала и что применяется третья теория прочности, условие прочности по которой

 .

Волокна в точке на верхней поверхности пластины растянуты, т. е. напряжения  положительны, поэтому следует обозначить:

.

Условие прочности примет вид

.