
- •Основные определения и допущения
- •Дифференциальное уравнение изогнутой срединной поверхности пластины в прямоугольных координатах
- •1.3. Цилиндрический и сферический изгиб пластины
- •1.4. Изгибающие моменты при осесимметричном изгибе круглой пластины
- •1.5 Дифференциальное уравнение изогнутой срединной поверхности круглой пластины
- •1.6. Граничные условия. Наибольшие напряжения и прогибы.
- •Расчет оболочек
- •2.1.Основные положения теории оболочек
- •2.2. Тонкостенная осесимметричная оболочка
- •2.3.Сферическая оболочка
- •2.4. Цилиндрическая оболочка
- •2.5. Коническая оболочка
- •2.6. Толстостенный цилиндр
- •2.7.Составные цилиндры. Общие положения
- •Список используемой литературы:
- •Александров а.В. Основы теории упругости и пластичности.
- •Потапов в.Д. Теория упругости и пластичности.
2.2. Тонкостенная осесимметричная оболочка
Тонкостенной осесимметричной называется оболочка, имеющая форму тела вращения толщина, которой мала по сравнению с радиусами кривизны ее поверхности (рис.33).
При расчете тонкостенных оболочек все нагрузки, действующие на них, прикладывают к срединной поверхности оболочки.
К тонким оболочкам могут быть отнесены такие часто встречающиеся элементы конструкций как резервуары, цистерны, газовые баллоны, корпуса аппаратов химических агрегатов и др.
При расчете таких элементов конструкций используется безмоментная теория оболочек, основные положения которой заключаются в следующем:
1. нагрузки, действующие на поверхности оболочки, могут считаться перпендикулярными им и симметричными относительно оси вращения оболочки;
2. вследствие малой толщины оболочки сопротивление изгибу отсутствует (изгибающий момент не возникает);
3. напряжения по толщине стенки оболочки распределены равномерно.
Из
оболочки, изображенной на рис.33 выделим
двумя меридиональными плоскостями ![]() и
и ![]() ,
(т.е. плоскостями проходящими
через ось симметрии оболочки), с
углом
,
(т.е. плоскостями проходящими
через ось симметрии оболочки), с
углом ![]() между
ними и двумя плоскостями, перпендикулярными
оси симметрии оболочки BC и AD,
элемент ABCD.
между
ними и двумя плоскостями, перпендикулярными
оси симметрии оболочки BC и AD,
элемент ABCD.
Радиусы
кривизны O2A и O2B элемента ABCD в
меридиональной плоскости обозначим
через R2,
а радиусы кривизны O1B и O1C в
плоскости, перпендикулярной меридиану,
обозначим через R1.
Нормальные напряжения, действующие по
боковым граням AB и CD,
соприкасающимся с меридиональными
плоскостями, называются окружными
напряжениями ![]() .
Нормальные напряжения, действующие по
боковым граням BС иAD,
называются меридиональными напряжениями
.
Нормальные напряжения, действующие по
боковым граням BС иAD,
называются меридиональными напряжениями ![]() .
Кроме напряжений
.
Кроме напряжений ![]() и
и ![]() на
элемент оболочки действует нагрузка в
виде давления
на
элемент оболочки действует нагрузка в
виде давления ![]() ,
перпендикулярного поверхности ABCD.
,
перпендикулярного поверхности ABCD.

Рис.33
Основным уравнением безмоментной теории оболочек является уравнение Лапласа, которое имеет следующий вид
![]() (8.1)
(8.1)
где ![]() -
толщина оболочки.
-
толщина оболочки.
Прежде чем перейдем к рассмотрению различных вариантов определения напряжений в оболочках остановимся на некоторых различиях, вызванных наличием газа или жидкости внутри оболочки.
В случае газового давления величина давления q постоянная во всех точках поверхности оболочки. Для резервуаров, наполненных жидкостью, значение q по их высоте переменно.
Для случая наполнения резервуара жидкостью необходимо учитывать, что если на какую-либо поверхность действует давление жидкости, то вертикальные составляющие сил давления равны весу жидкости в объеме, расположенном над поверхностью. Поэтому давление жидкости в различных сечениях оболочки будет различным, в отличие от давления газа.
Определим напряжения в сферических и цилиндрических оболочках т.к. они наиболее часто используются в промышленности.
2.3.Сферическая оболочка
Отсечем
часть сферической оболочки нормальным
коническим сечением с углом ![]() при
вершине и рассмотрим равновесие этой
части оболочки вместе с заключенной в
ней жидкостью с удельным весом
при
вершине и рассмотрим равновесие этой
части оболочки вместе с заключенной в
ней жидкостью с удельным весом ![]() .
Сферическую часть отделим от основной
оболочки плоскостью, перпендикулярной
оси симметрии.
.
Сферическую часть отделим от основной
оболочки плоскостью, перпендикулярной
оси симметрии.
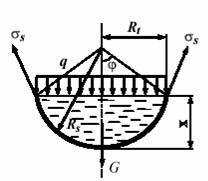
Рис.34
На
рис.34 изображена расчетная схема
сферической оболочки радиусом Rs.
Высота отсеченной поверхности ![]() .
Давление q на
отсеченную часть в этом и последующих
случаях равно
весу жидкости в объеме, расположенном
над поверхностью, который равен
.
Давление q на
отсеченную часть в этом и последующих
случаях равно
весу жидкости в объеме, расположенном
над поверхностью, который равен
![]() , (8.2)
, (8.2)
где ![]() -
высота столба жидкости выше отсеченной
части оболочки.
-
высота столба жидкости выше отсеченной
части оболочки.
Уравнение равновесия отсеченной части может быть записано, как сумма проекций всех сил на вертикальную ось
![]() . (8.3)
. (8.3)
В данном уравнении величина G – вес жидкости, заполняющей отсеченную часть сферической оболочки (см. рис.34).
![]() , (8.4)
, (8.4)
где ![]() -
объем нижней отсеченной части сферической
оболочки.
-
объем нижней отсеченной части сферической
оболочки.
Путем интегрирования объем сферического сегмента может быть определен по формуле
![]() . (8.5)
. (8.5)
После подстановки уравнения (8.5) в выражение (8.4), и затем, в (8.3), получим конечное уравнение равновесия для сферической части сегмента
![]() . (8.6)
. (8.6)
Из
этого уравнения можно определить
величину меридионального напряжения ![]() ,
и, после подстановки в уравнение Лапласа
(16.1), найти величину окружного напряжения
,
и, после подстановки в уравнение Лапласа
(16.1), найти величину окружного напряжения ![]() .
.
