5.3.3. Вторая интерполяционная формула Ньютона

Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую формулу становиться невыгодно. В этом случае применяется формула для интерполирования назад – вторая интерполяционная формула Ньютона, которая отыскивается в виде:

(13)

Как и для первой формулы Ньютона, коэффициенты находится из условия совпадения значений функций и интерполяционного многочлена в узлах интерполяции:

(14)

Поставляя (14) в (13) и используя обозначение получим окончательный вид второй интерполяционной формулы Ньютона:

(15)

5.4. Интерполяция сплайнами

При большом количестве узлов интерполяции сильно возрастает степень интерполяционных многочленов, что делает их неудобными для вычислений. Высокой степени многочлена можно избежать, разбив отрезок интерполяции на несколько частей, а затем построить на каждой из них самостоятельный интерполяционный многочлен.

Однако такое интерполирование приобретает существенный недостаток: в точках стыковки различных интерполяционных многочленов будет разрывная их первая производная. В этом случае удобно пользоваться особым видом кусочно-полиномиальной интерполяции – интерполяции сплайнами (spline – рейка).

Сплайн – это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе неполными своими производными.

Рассмотрим способ построения сплайнов третьей степени (так называемых кубических сплайнов), наиболее широко распространенных на практике. Пусть функция задана таблицей:

x	x0	x1	x2	…	xn
f(x)	y0	y1	y2	…	yn

Длину частичного отрезка [x_i-1, x_i] обозначим через h=x_i-x_i-1 i=1, 2,…., n.

Будем искать кубический сплайн на каждом из частичных отрезков [x_i-1, x_i] в виде:

(16)

_{где ai, bi, ci, di – неизвестные коэффициенты. Так как для каждого отрезка строится свой многочлен, а всего отрезков n, то общее количество неизвестных коэффициентов – 4n.}

Потребуем совпадения значений S(x) в узлах и табличными значениями функций f: подставим в многочлены (16) значения x_i-1, должны, соответственно, получить значения y_i-1.

(17)

Подставляя значения x_i, получим y_i:

(18)

Число уравнений вида (17) и (18) 2n – вдвое меньше числа неизвестных коэффициентов. Чтобы получить дополнительные условия потребуем также непрерывности первой и второй производных и во всех точках, включая узлы. Для этого следует приравнять левые и правые производные во внутреннем узле x_i. В начале найдем и :

Определим левые и правые производные:

(вместо i подставим i+1)

Аналогично для второй производной получаем:

Приравнивая, левые и правые производных, получаем:

(19) (20)

Последние два уравнения дают 2(n-1) условия. Недостает еще двух условий.

Обычно в качестве этих условий берут требования к поведению сплайна в крайних точках интерполяции x₀ и x_n.

Потребуем нулевой кривизны сплайна в конечных точках (т.е. равенства вторых производных слева и справа), получим:

(21)

Перепишем все уравнения, учитывая, что :

(22)

Система (22) состоит из 3n уравнений с 3n неизвестными. Решив ее, получим значения неизвестных , определяющих совокупность всех формул для искомого сплайна.

Пример:

Интерполяционная функция задана таблицей:

x	2	3	5	7
f(x)	4	-2	6	-3

Определить кубический сплайн на трех отрезках [2;3], [3;5], [5;7].

Решение:

1. Определим длину каждого отрезка (h_i):

отрезок отрезок отрезок

Тогда искомый сплайн будет иметь вид:

2. Составим систему уравнений вида (22). Первая группа уравнений состоит из трех уравнений:

По следующим двум уравнениям системы (22) получим еще две группы из двух уравнений:

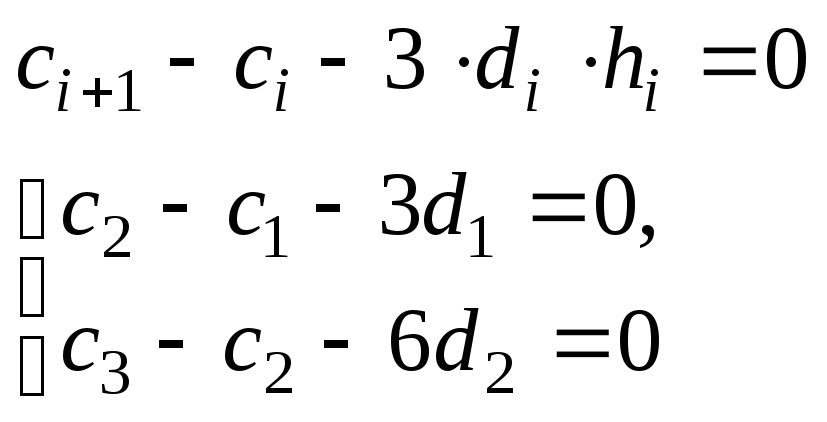
Последние два уравнения получим так же, пользуясь системой (22):

Таким образом, получили систему из 9 уравнений с 9 неизвестными:

Составим матрицу этой системы:

Решим данную систему и получим:

Полученные коэффициенты определяют искомый сплайн:

Вычислим значение функции в какой-либо точке, например в точке х=4.3. Так как эта точка принадлежит второму отрезку, подставим данное значение в S₂:

Построим графики исходной и полученной зависимостей, а также покажем полученную точку: