
- •Раздзел 4. Інтэгральнае злічэнне. §4.1. Азначэнне і ўласцівасці нявызначанага інтэграла.
- •1° Азначэнне нявызначанага інтэграла.
- •Тэарэма 1 (пра агульны выгляд першаіснай). Няхай функцыя ёсць першаісная для на х. Функцыя ёсць таксама першаісная для , калі і толькі калі .
- •2° Уласцівасці нявызначанага інтэграла.
- •§4.2. Асноўныя метады інтэгравання.
- •1º. Метад падстановы.
- •Тэарэма 1. Калі функцыя мае першаісную на прамежку т, а функцыя ёсць дыферэнцавальная на х, прычым , то
- •2º. Метад інтэгравання часткамі.
- •§4.4. Метад рацыяналізацыі.
- •1º. Інтэграванне дробава-лінейнай ірацыянальнасці.
- •2º. Інтэграванне біномнага дыферэнцыяла.
- •3º. Інтэграванне рацыянальна-трыганаметрычных функцый.
- •4º. Інтэграванне квадратовых ірацыянальнасцяў.
- •§4.5. Азначэнне і ўмовы існавання вызначанага інтэграла.
- •Прыклад 1. Вылічыць
- •Прыклад 2. Вылічыць паводле азначэння .
- •Заўвага. Абмежаванасць ёсць недастатковая ўмова для інтэгравальнасці функцыі.
- •Крытэр інтэгравальнасці. Для таго каб функцыя , вызначаная і абмежаваная на адрэзку , была інтэгравальнаю на гэтым адрэзку, неабходна і дастаткова, каб гэтая функцыя адпавядала ўмове
- •§4.6. Класы інтэгравальных функцый.
- •Тэарэма 1 (Інтэгравальнасць непарыўнай функцыі). Непарыўная на адрэзку функцыя ёсць інтэгравальная на гэтым адрэзку.
- •§4.8. Ацэнкі інтэгралаў.
- •Вынік 2 (Тэарэма пра пасярэдняе значэнне непарыўнай функцыі). Калі функцыя ёсць непарыўная, то існуе лік такі, што
- •1º. Формула Ньютана-Ляйбніца.
- •2º. Замена зменнай .
- •3º. Інтэграванне часткамі.
- •4º. Інтэграванне цотнай, няцотнай і перыядычнай функцый.
- •1º.Плошча плоскай фігуры.
- •Прыклад 1. Вылічыць плошчу фігуры, абмежаванай крывымі і .
- •Прыклад 2. Вылічыць плошчу фігуры, абмежаванай крывой . ►Спачатку зробім рысунак фігуры
- •2º. Даўжыня крывой.
- •Прыклад 3. Вылічыць даўжыню адной аркі цыклоіды (акружына радыюса коціцца па восі абцысаў).
- •3º. Аб’ём цела авароту.
- •Прыклад 5. Вылічыць аб’ём тора, г. Зн. Цела, якое атрымліваецца ад авароту круга радыюса вакол восі, што ляжыць у плоскасці гэтага круга на адлегласці ад яго цэнтра.
- •§4.13. Інтэграл па бясконцым прамежку (ні-1).
- •Прыклад 1. Вылічыць .
- •Тэарэма 2 (лімітавая прыкмета параўнання). Няхай функцыя а і няхай . Тады:
- •Калі ёсць збежны і , то – таксама збежны;
- •2) Калі ёсць разбежны і , то – разбежны.
- •Прыклады. А) збежны, бо .
- •§4.15. Умоўная збежнасць ні-1.
- •Тэарэма 1 (Прыкмета Дырыхле). Няхай функцыя ёсць непарыўная і мае абмежаваную першаісную на . Няхай функцыя ёсць непарыўна дыферэнцавальная і манатонная на і . Тады інтэграл – збежны.
- •Тэарэма 2 (прыкмета Абэля). Калі функцыя ёсць непарыўная на і – збежны, а функцыя абмежаваная і яе вытворная – непарыўная і не мяняе знаку на , то – збежны.
- •Прыклад 1. Даследаваць на абсалютную збежнасць інтэграл .
- •Прыклад 2. Даследуем інтэграл Фрэнэля на збежнасць.
- •§4.16. Неўласцівыя інтэгралы ад неабмежаваных функцый.
Прыклады. А) збежны, бо .
б)
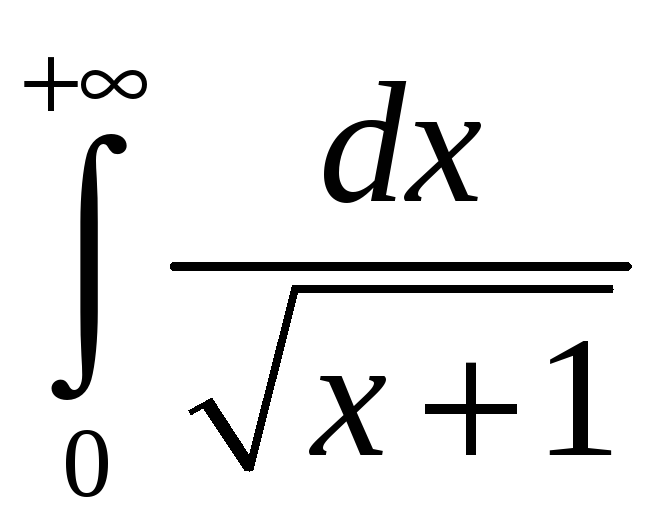 разбежны, бо
разбежны, бо
 .
.
в)
 збежны, бо
збежны, бо
![]() нарастае хутчэй за любую ступень, таму
нарастае хутчэй за любую ступень, таму
![]() .
Такім чынам,
.
Такім чынам,
Практыкаванне.
Дакажыце, што
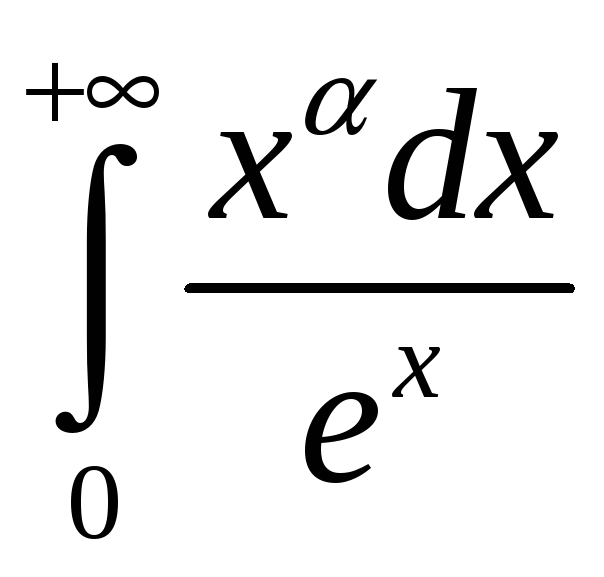 збежны пры
збежны пры
![]() .
.
г)
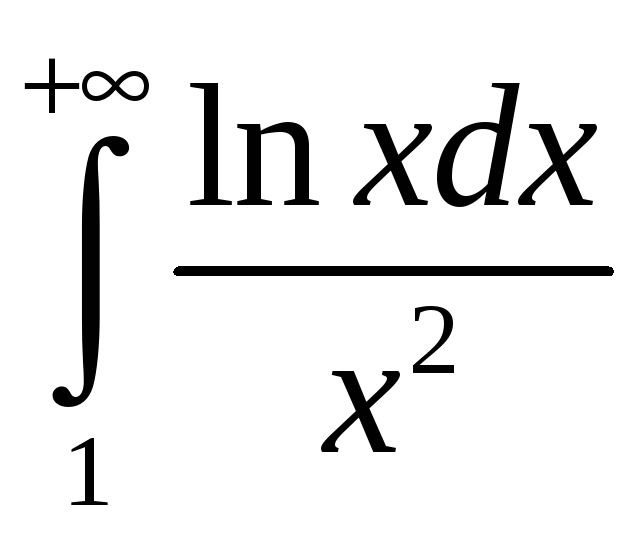 збежны, бо
збежны, бо
![]() – лянівая функцыя, таму
– лянівая функцыя, таму
![]() .
Такім чынам,
.
Такім чынам,
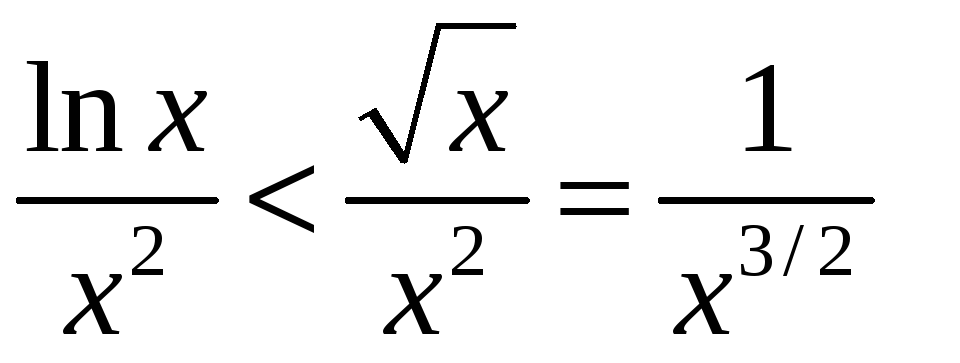 .
.
Практыкаванне.
Дакажыце, што
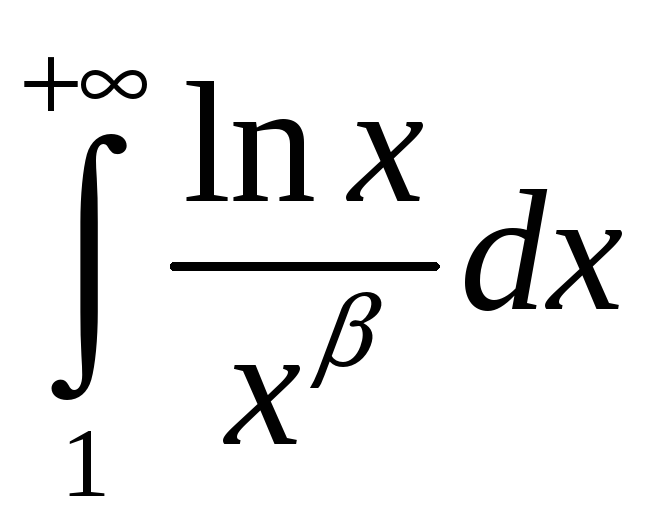 збежны пры
збежны пры
![]() .
.
def.
Неўласцівы інтэграл
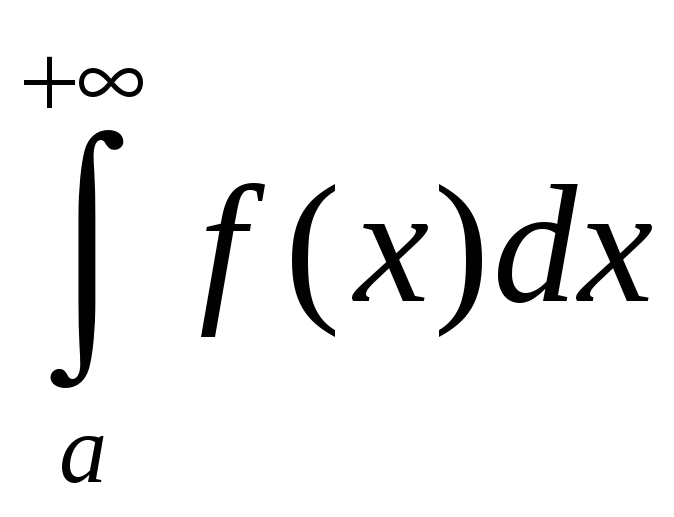 называецца абсалютна
збежным,
калі ін-тэграл
называецца абсалютна
збежным,
калі ін-тэграл
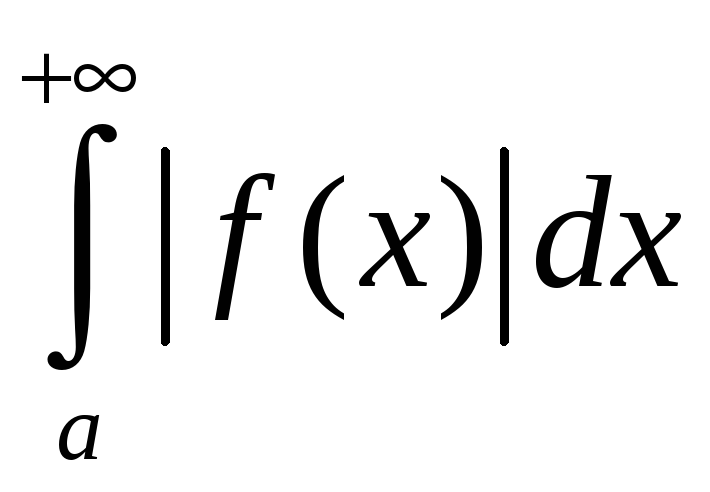 ёсць збежны.
ёсць збежны.
Заўвага
3.
З абсалютнай збежнасці НІ-1 вынікае яго
збежнасць, паколькі
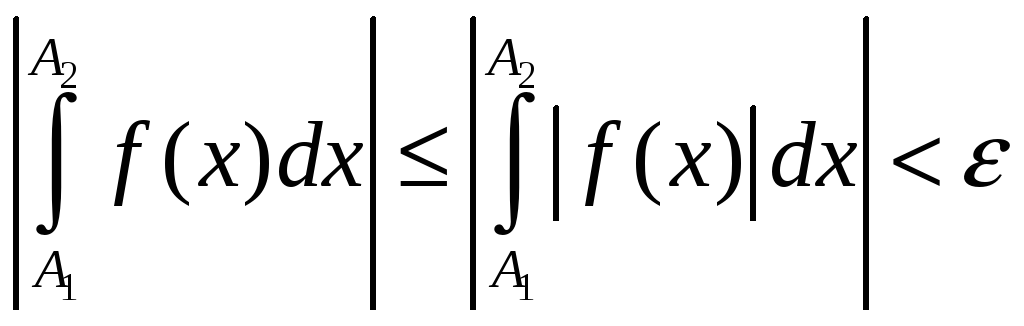 ,
г. зн. выконваецца крытэр Кашы.
,
г. зн. выконваецца крытэр Кашы.
§4.15. Умоўная збежнасць ні-1.
def.
Калі інтэграл
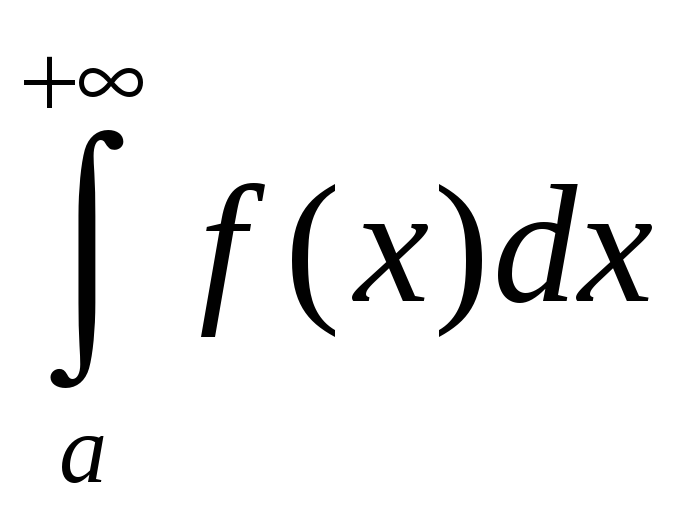 ёсць збежны, а
ёсць збежны, а
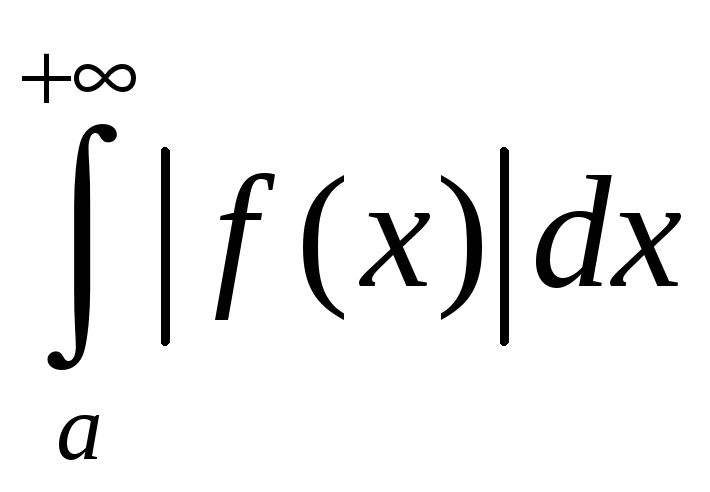 – разбежны, то інтэграл
– разбежны, то інтэграл
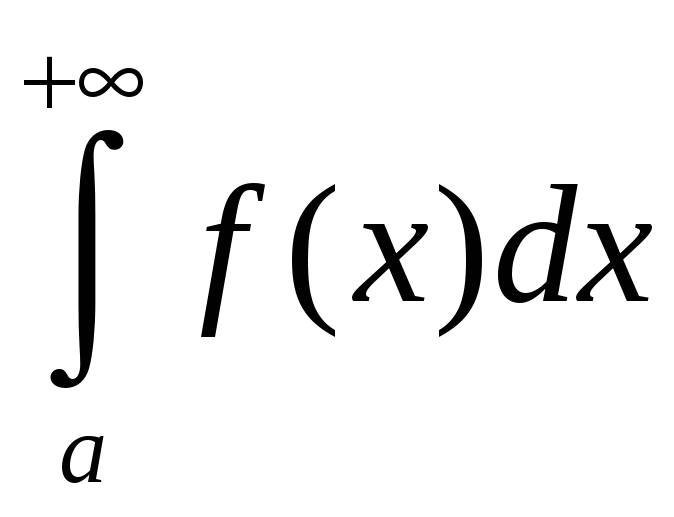 называецца ўмоўна
збежным.
называецца ўмоўна
збежным.
Тэарэма 1 (Прыкмета Дырыхле). Няхай функцыя ёсць непарыўная і мае абмежаваную першаісную на . Няхай функцыя ёсць непарыўна дыферэнцавальная і манатонная на і . Тады інтэграл – збежны.
□ Пераканаемся,
што для функцыі
![]() выконваецца крытэр інтэгра-вальнасці
Кашы. Правядзем інтэграванне часткамі
выконваецца крытэр інтэгра-вальнасці
Кашы. Правядзем інтэграванне часткамі

Паколькі
![]() абмежаваная, то
абмежаваная, то
![]() ,
прычым
,
прычым
![]() .
Такім чынам, маем
.
Такім чынам, маем

Паколькі
![]() ,
то
,
то
![]() .
Таму
.
Таму
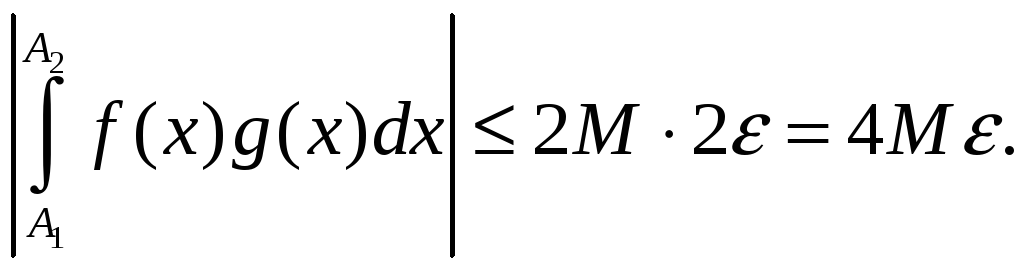
Згодна
з крытэрам Кашы інтэграл
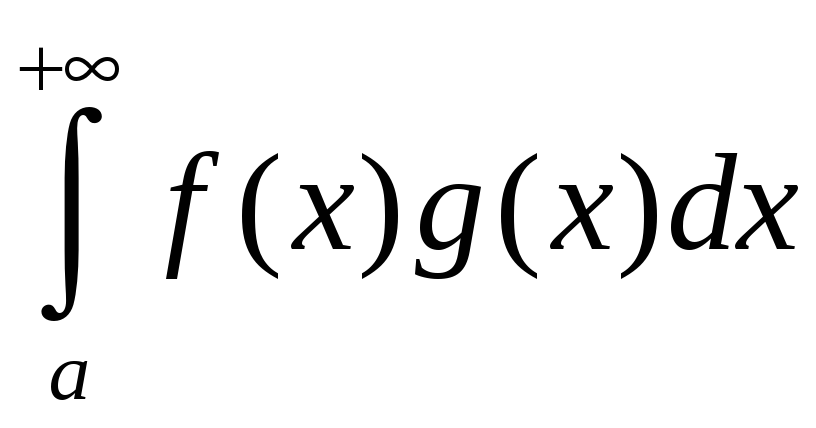 – збежны. ■
– збежны. ■
Тэарэма 2 (прыкмета Абэля). Калі функцыя ёсць непарыўная на і – збежны, а функцыя абмежаваная і яе вытворная – непарыўная і не мяняе знаку на , то – збежны.
□ Доказ
вынікае з прыкметы Дырыхле. Паколькі
вытворная функцыі
![]() не мяняе знаку, то яна манатонная на
не мяняе знаку, то яна манатонная на
![]() ,
а тады з яе абмежаванасці вынікае
існаванне ліміта
,
а тады з яе абмежаванасці вынікае
існаванне ліміта
![]() .
З роўнасці
.
З роўнасці
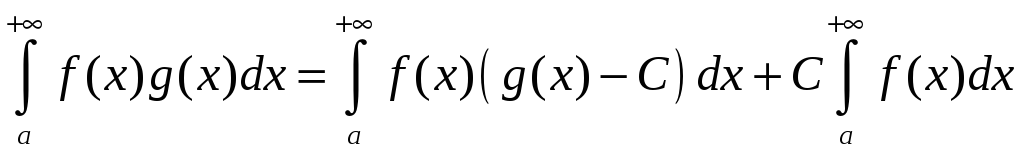
вынікае:
дастаткова даказаць збежнасць
 .
.
Паколькі
![]() і функцыя
і функцыя
![]() – манатонная,
то, каб скарыстацца прыкметаю Дырыхле,
дастаткова даказаць, што першаісная
для
– манатонная,
то, каб скарыстацца прыкметаю Дырыхле,
дастаткова даказаць, што першаісная
для
![]() ёсць абмежаваная.
ёсць абмежаваная.
Сапраўды,
паколькі інтэграл
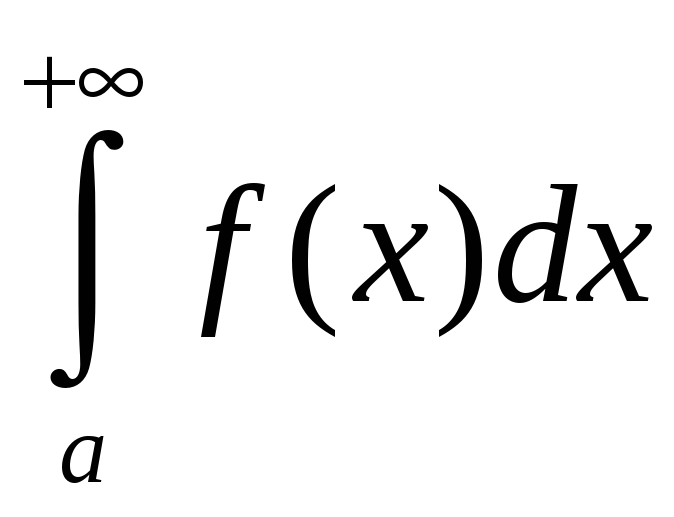 – збежны, то існуе ліміт
– збежны, то існуе ліміт
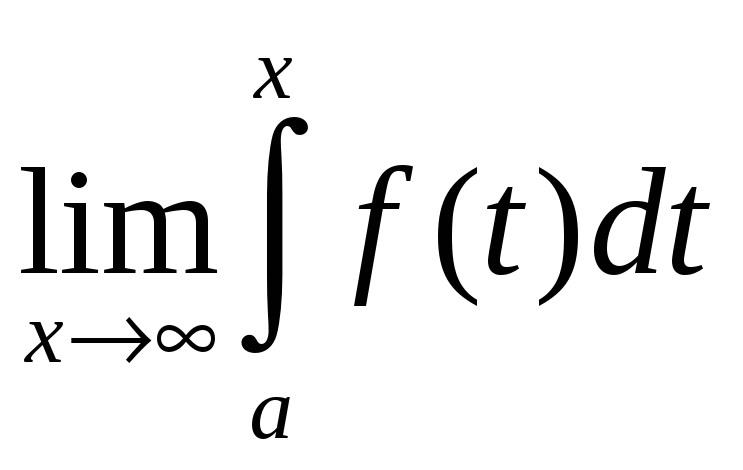 ,
а інтэграл
,
а інтэграл
 – першаісная для непарыўнай функцыі
– першаісная для непарыўнай функцыі
![]() ёсць функцыя непарыўная на любым адрэзку
ёсць функцыя непарыўная на любым адрэзку
![]() .
Паколькі ліміт гэтай функцыі існуе на
.
Паколькі ліміт гэтай функцыі існуе на
![]() ,
то яна – абмежаваная на
,
то яна – абмежаваная на
![]() .
■
.
■
Прыклад 1. Даследаваць на абсалютную збежнасць інтэграл .
► Першаісная
функцыі
![]() ёсць
ёсць
![]() – абмежаваная, а функцыя
– абмежаваная, а функцыя
![]() –
манатонная і бясконца малая на прамежку
–
манатонная і бясконца малая на прамежку
![]() .
Паводле прыкметы Дырыхле інтэграл
.
Паводле прыкметы Дырыхле інтэграл
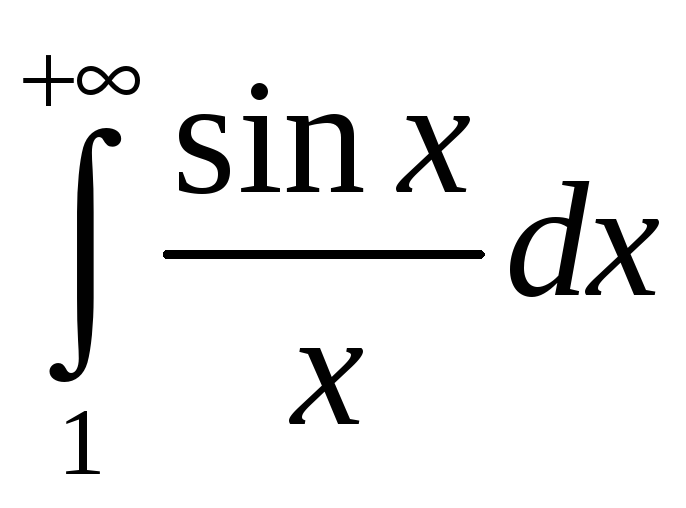 – збежны.
– збежны.
Даследуем
інтэграл на абсалютную збежнасць. З
няроўнасці
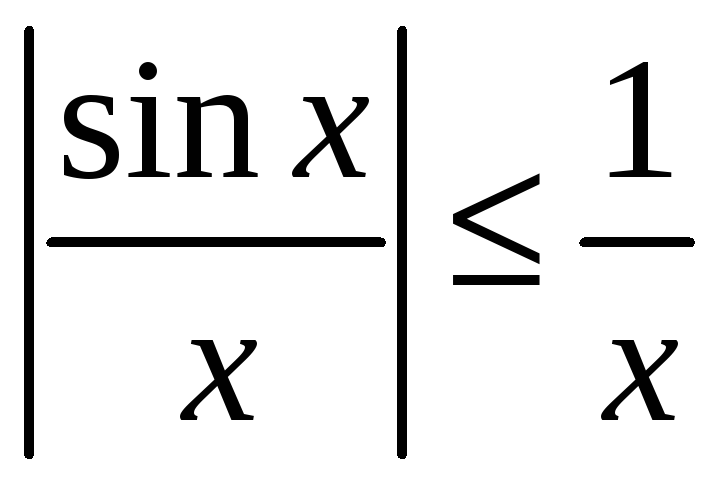 нічога не вынікае. Але
нічога не вынікае. Але
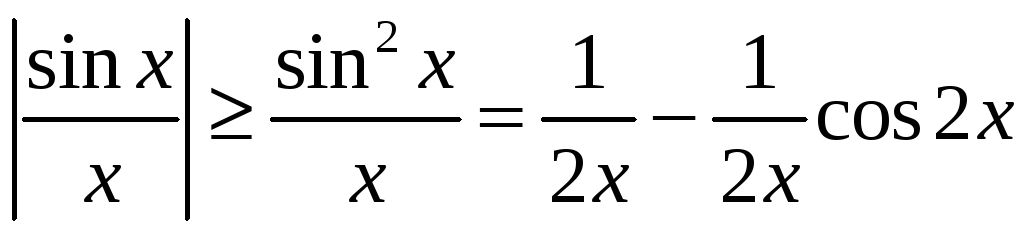 і пры гэтым інтэграл
і пры гэтым інтэграл
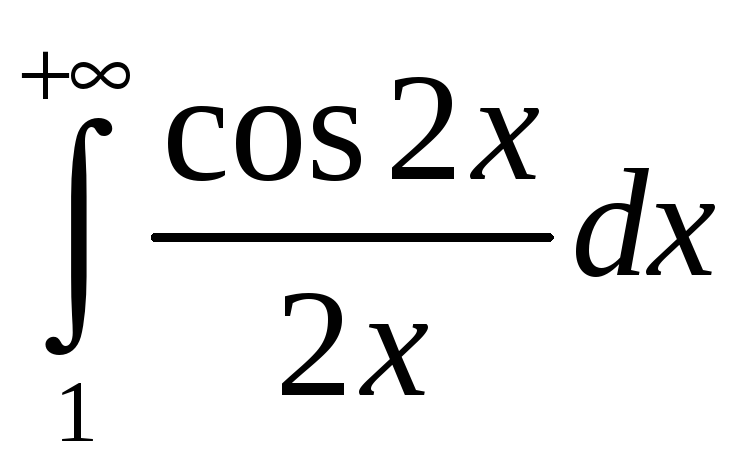 паводле прыкметы Дырыхле ёсць збежны.
паводле прыкметы Дырыхле ёсць збежны.
Калі б
інтэграл
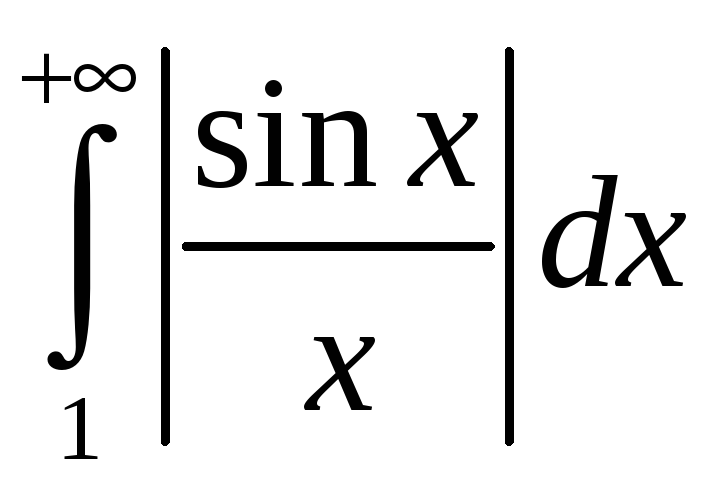 быў збежны, то з няроўнасці
быў збежны, то з няроўнасці
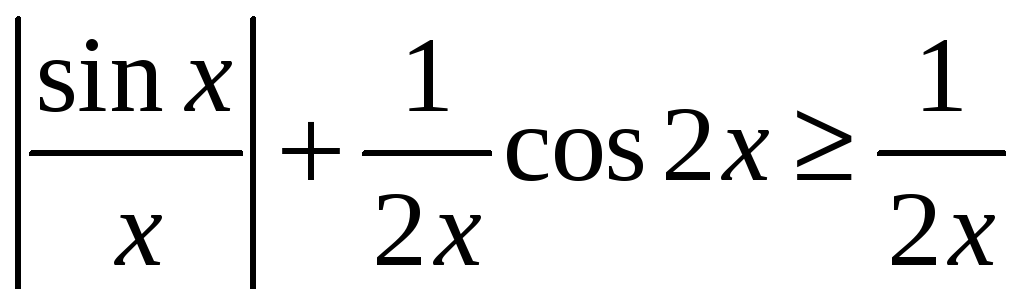 мелі б, што
мелі б, што
![]() – збежны, але ж ён разбежны. Такім чынам,
– збежны, але ж ён разбежны. Такім чынам,
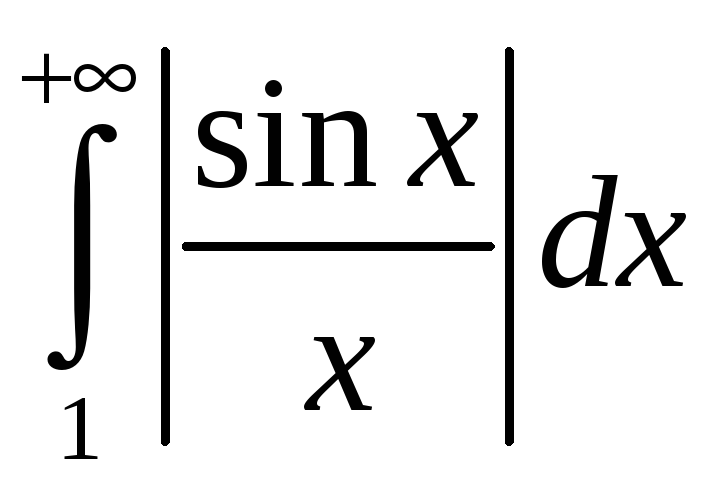 – разбежны, а інтэграл
– разбежны, а інтэграл
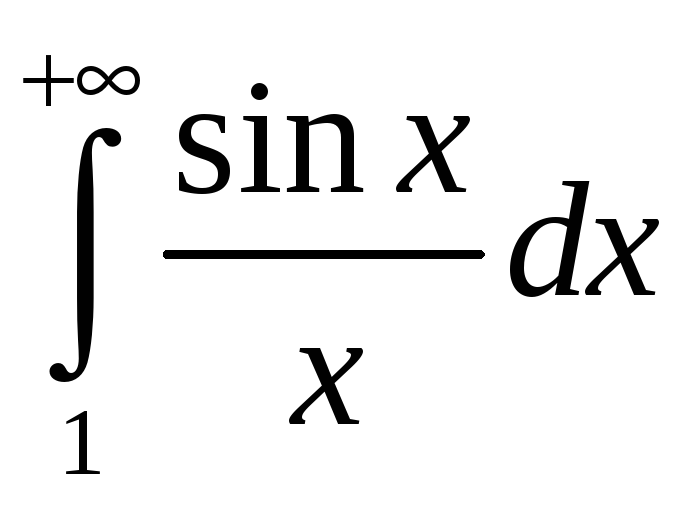 – умоўна збежны.
◄
– умоўна збежны.
◄
Прыклад 2. Даследуем інтэграл Фрэнэля на збежнасць.
►Запішам
падынтэгральную функцыю у выглядзе
![]() .
Паколькі першаісная
.
Паколькі першаісная
![]() – абмежаваная, а функцыя
– абмежаваная, а функцыя
![]() манатонна імкнецца да нуля, то на падставе
прыкметы Дырыхле інтэграл Фрэнэля –
збежны.
манатонна імкнецца да нуля, то на падставе
прыкметы Дырыхле інтэграл Фрэнэля –
збежны.
Зазначым,
што інтэграл
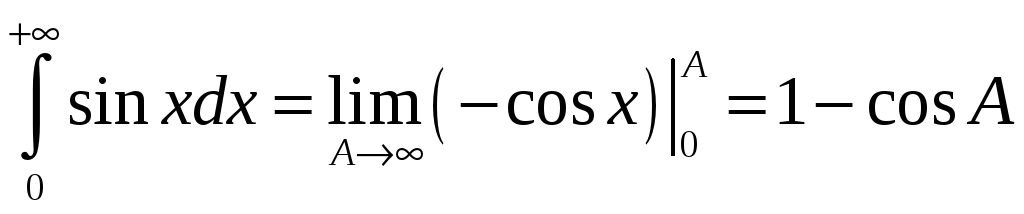 – разбежны. ◄
– разбежны. ◄
§4.16. Неўласцівыя інтэгралы ад неабмежаваных функцый.
def.
Калі функцыя
![]() ёсць неабмежаваная ў пункце
ёсць неабмежаваная ў пункце
![]() ,
і інтэгравальная на кожным адрэзку
,
і інтэгравальная на кожным адрэзку
![]() ( упрыватнасці
( упрыватнасці
![]() ёсць абмежаваная на адрэзку
ёсць абмежаваная на адрэзку
![]() ),
то пункт
),
то пункт
![]() называюць асаблівым
пунктам
функцыі
называюць асаблівым
пунктам
функцыі
![]() .
.
def. Ліміт
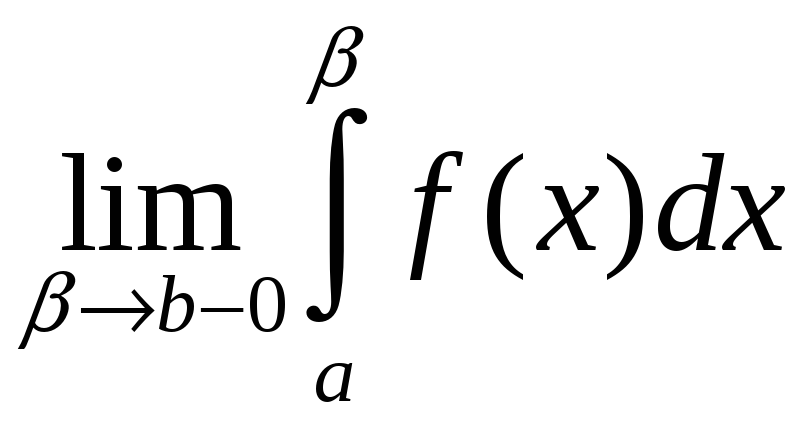 (1)
(1)
называюць
неўласцівым
інтэгралам ад неабмежаванай функцыі
на адрэзку
![]() (або
неўласцівым
інтэгралам другога роду,
НІ-2) і абазначаюць
(або
неўласцівым
інтэгралам другога роду,
НІ-2) і абазначаюць
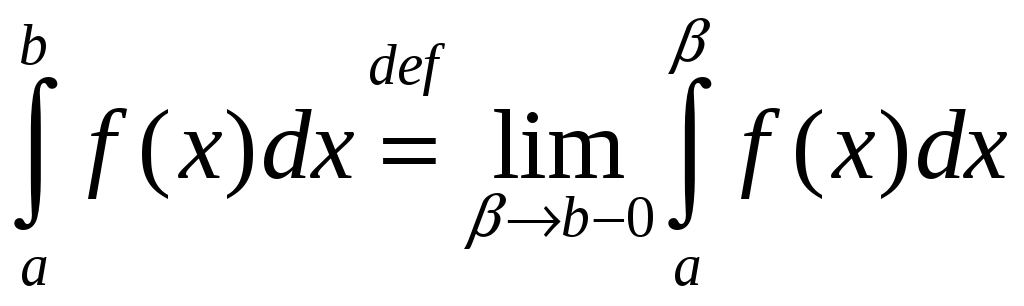 .
(2)
.
(2)
Калі існуе канечны ліміт (1), то Ні-2 (2) называюць збежным. Калі ж ліміт (1) не існуе, то кажуць, што інтэграл (2) ёсць разбежны.
Заўвага
1.
Калі
![]() ,
то інтэгралы
,
то інтэгралы
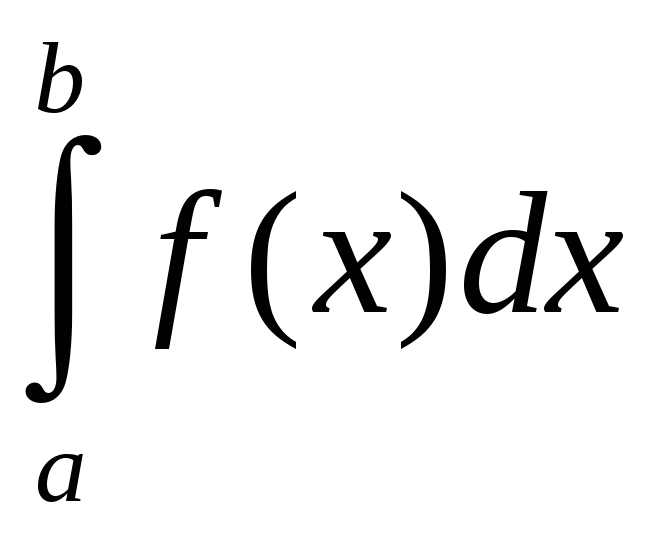 і
і
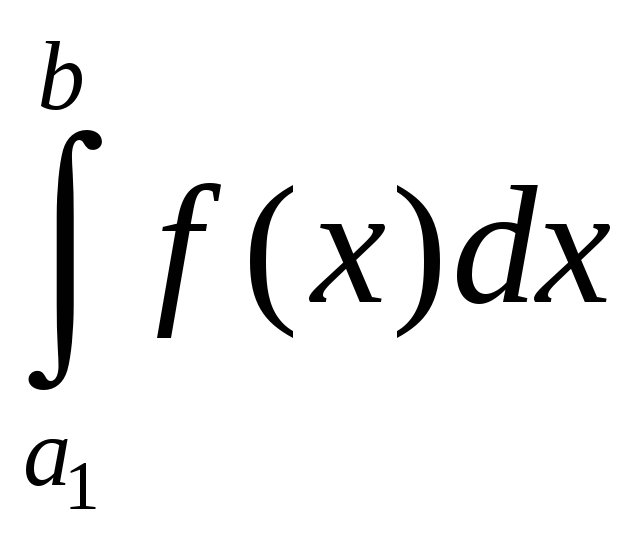 збягаюцца або разбягаюцца адначасова.
збягаюцца або разбягаюцца адначасова.
Заўвага 2. Формулу (2) бывае больш зручна запісваць у выглядзе
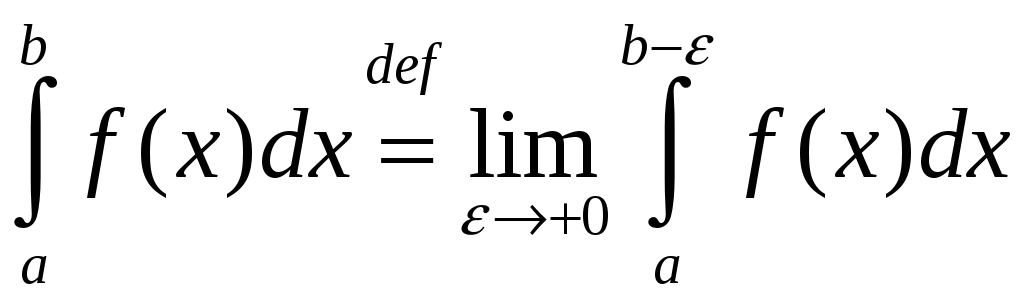 .
(3)
.
(3)
Аналагічна
азначаецца неўласцівы інтэграл
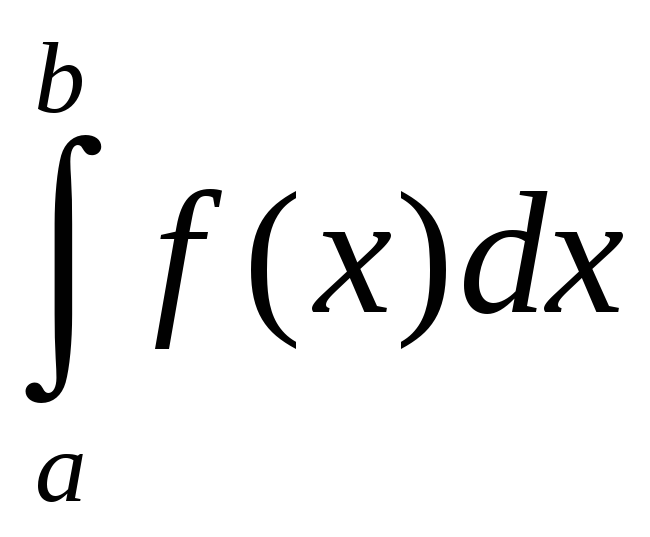 ,
калі
,
калі
![]() ёсць асаблівы пункт функцыі
ёсць асаблівы пункт функцыі
![]()
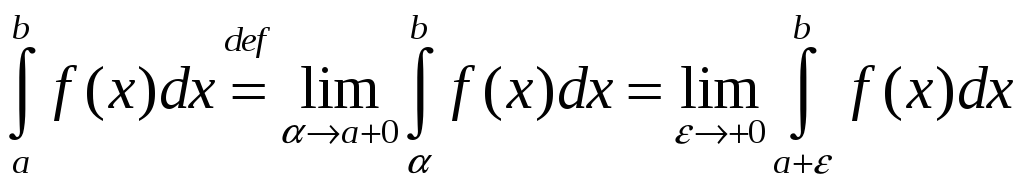 .
.
Калі ж
пункт
![]() ёсць асаблівы пункт функцыі
ёсць асаблівы пункт функцыі
![]() ,
і інтэгралы
,
і інтэгралы
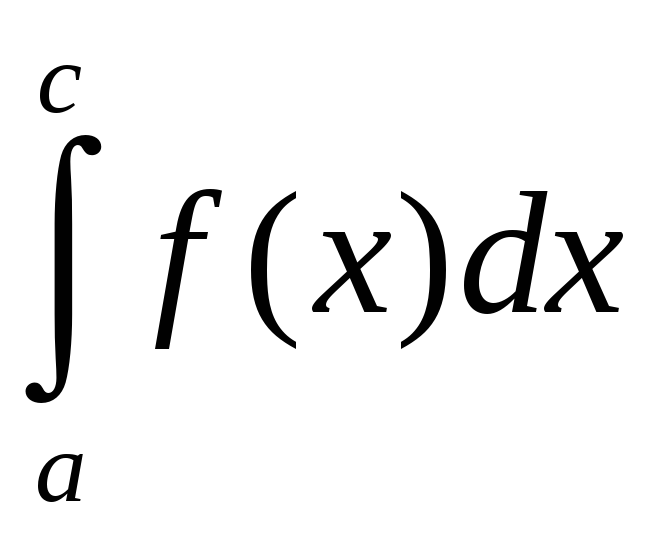 і
і
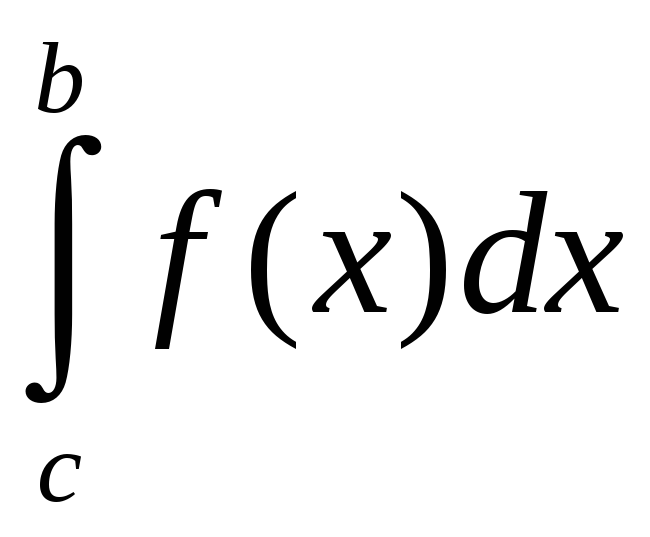 – збежныя, то
– збежныя, то
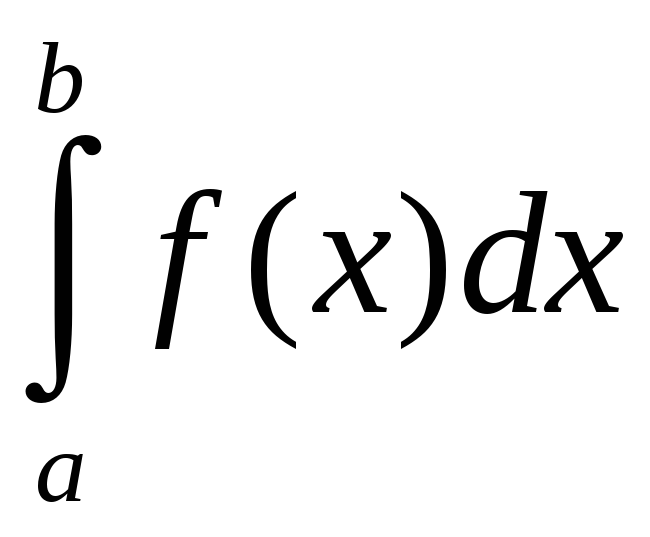 =
=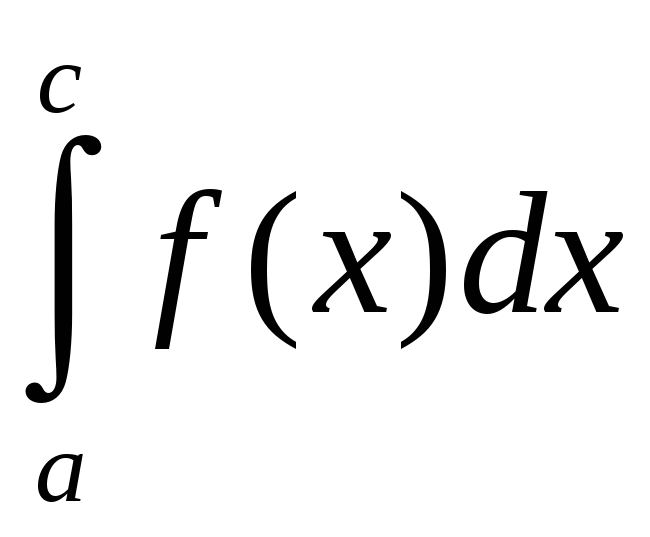 +
+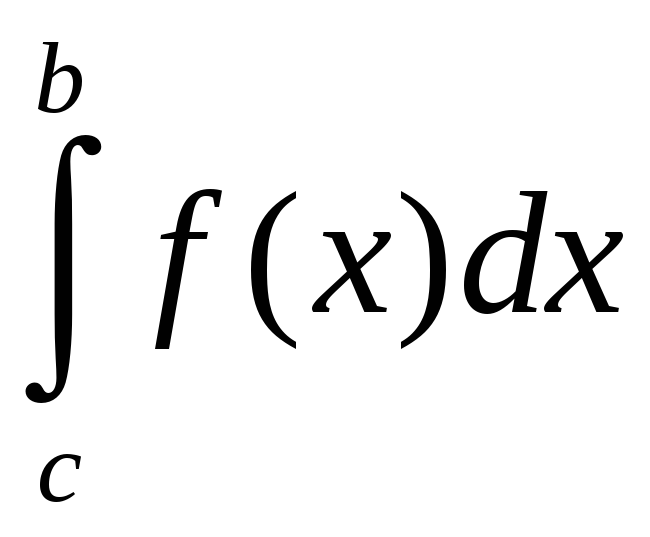 .
.
Далей для пэўнасці мы будзем вывучаць НІ-2, якія азначаюцца формуламі (2), або (3).
Паміж НІ-1 і НІ-2 існуе пэўная сувязь.
Сапраўды,
няхай
![]() ёсць інтэгравальная на
ёсць інтэгравальная на
![]() і
і
![]() – яе асаблівы пункт. У інтэграле з (3)
– яе асаблівы пункт. У інтэграле з (3)
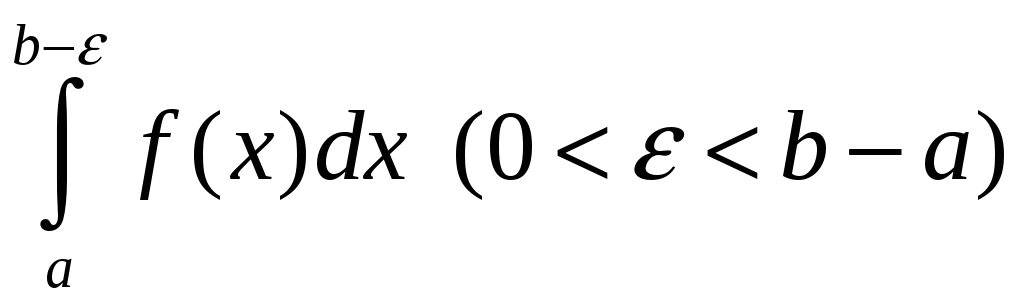 зробім замену
зробім замену
![]()
і атрымаем
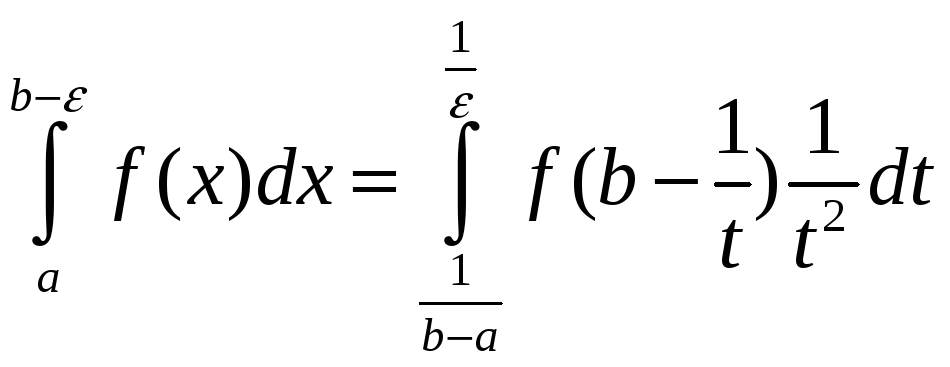 .
Такім чынам, прыходзім да роўнасці
.
Такім чынам, прыходзім да роўнасці
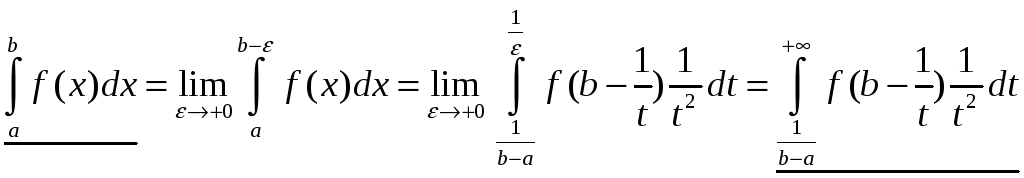 .
.
Гэта
азначае, што для НІ-2 праўдзяцца
ўласцівасці, аналагічныя адпаведным
уласцівасцям для НІ-1, а на збежнасць
НІ–2 можна даследаваць як НІ–1, які
атрымліваецца з яго пасля замены
![]() .
.
Прыклад 1.
Даследуем
на збежнасць
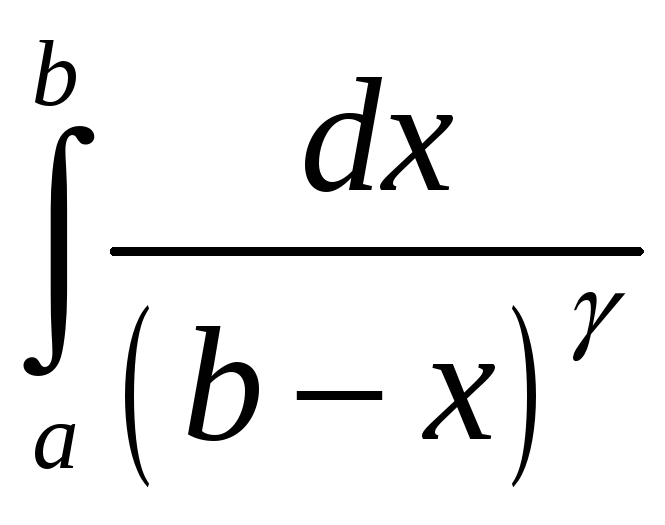 .
.
► Калі ў гэтым інтэграле зрабіць вышэй згаданую замену
![]() ,
,
то мы
прыходзім да інтэграла
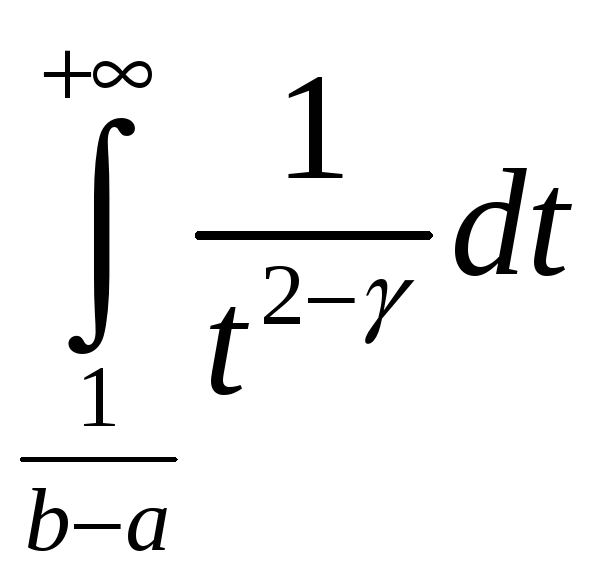 ,
які ёсць збежны толькі пры
,
які ёсць збежны толькі пры
![]() або
або
![]() .
Такім чынам, разгляданы намі інтэграл
ёсць збежны пры
.
Такім чынам, разгляданы намі інтэграл
ёсць збежны пры
![]() і разбежны пры
і разбежны пры
![]() .
У прыватнасці,
.
У прыватнасці,
![]() ёсць збежны толькі пры
ёсць збежны толькі пры
![]() .
◄
.
◄
Аналагічна, як і для НІ-1 можна даказаць наступныя тэарэмы.
Тэарэма 1
(прыкмета
параўнання).
Няхай
![]() .
Калі
.
Калі
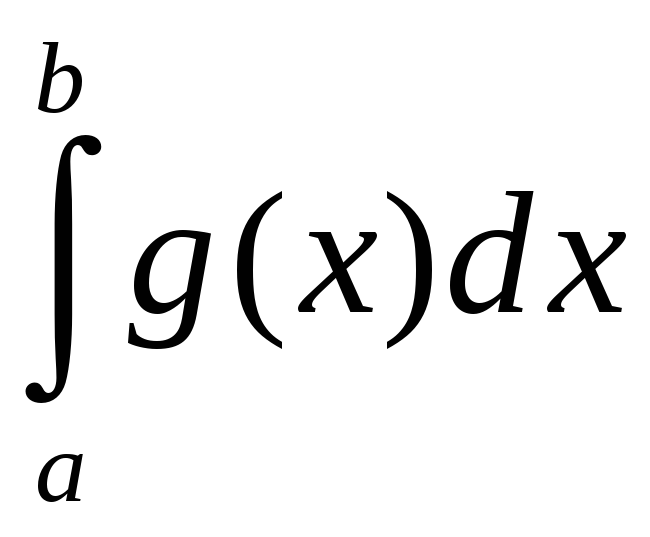 ёсць збежны, то
ёсць збежны, то
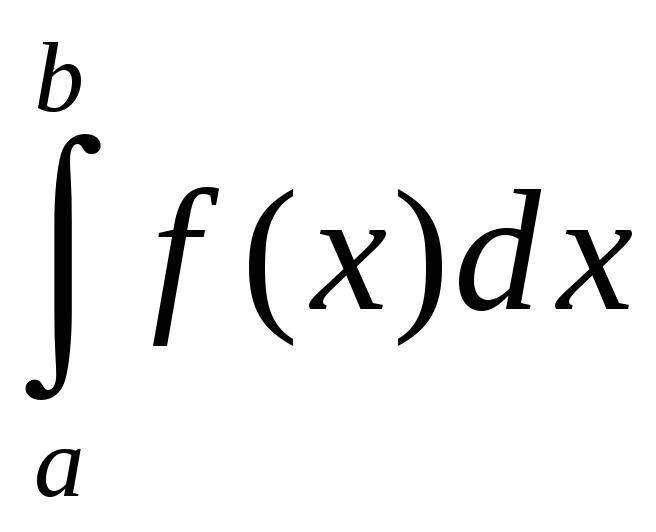 таксама збежны. Калі ж
таксама збежны. Калі ж
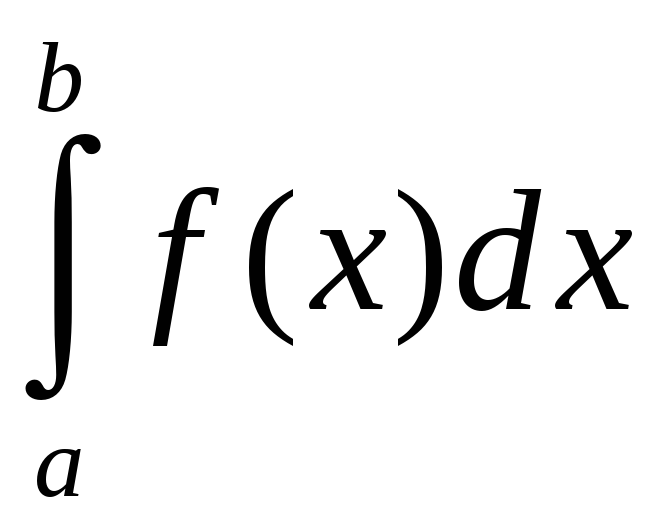 разбежны, то
разбежны, то
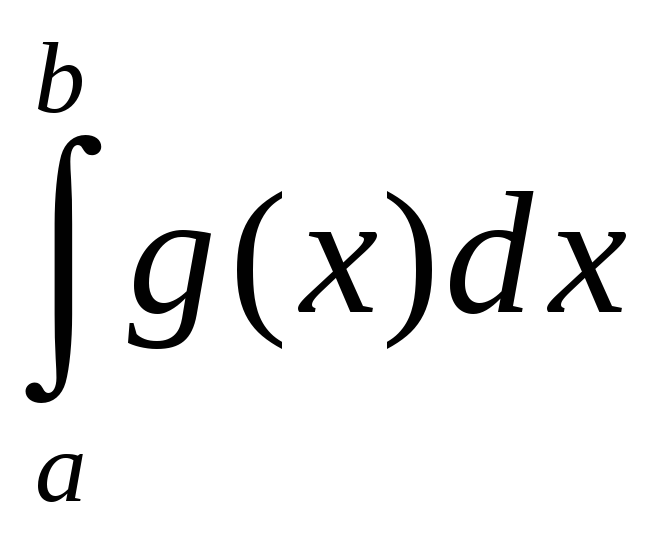 таксама
разбежны
.
таксама
разбежны
.
Тэарэма 2
(лімітавая
прыкмета параўнання).
Калі функцыі
![]() і
і
![]() і мае месца
і мае месца
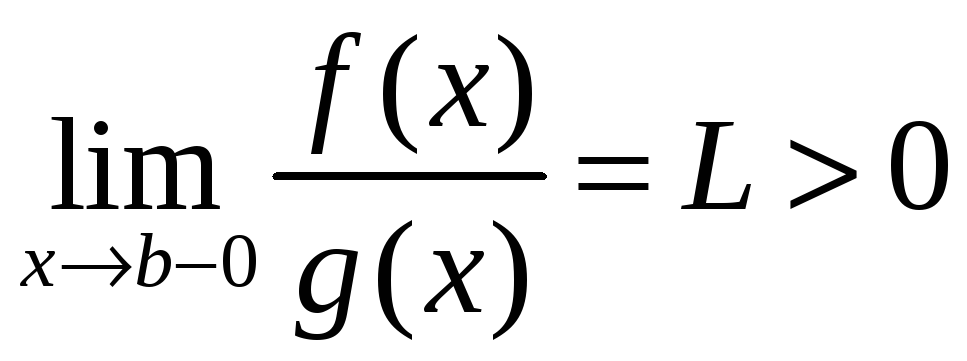 то абодва інтэгралы
то абодва інтэгралы
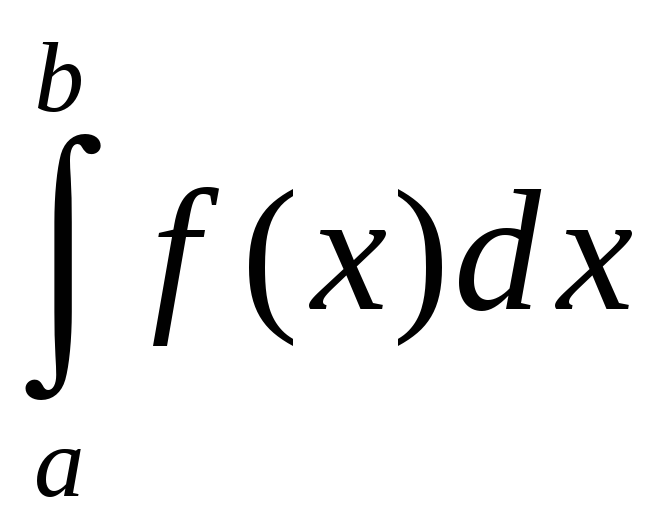 і
і
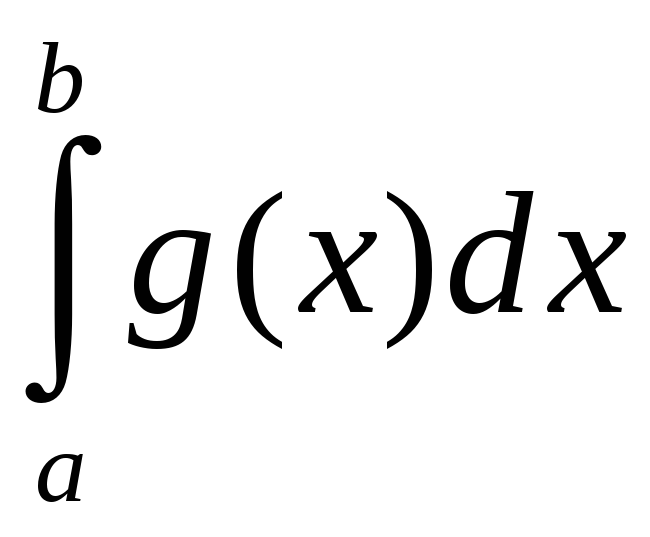 збягаюцца або разбягаюцца адначасова.
У прыватнасці гэта мае месца, калі
збягаюцца або разбягаюцца адначасова.
У прыватнасці гэта мае месца, калі
![]() .
.
Вынік
Калі
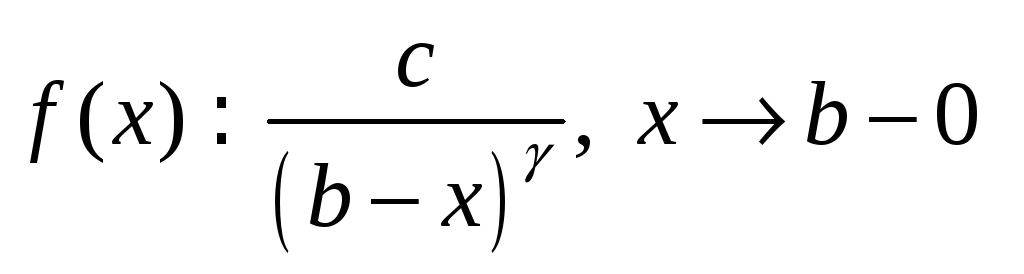 ,
то
,
то
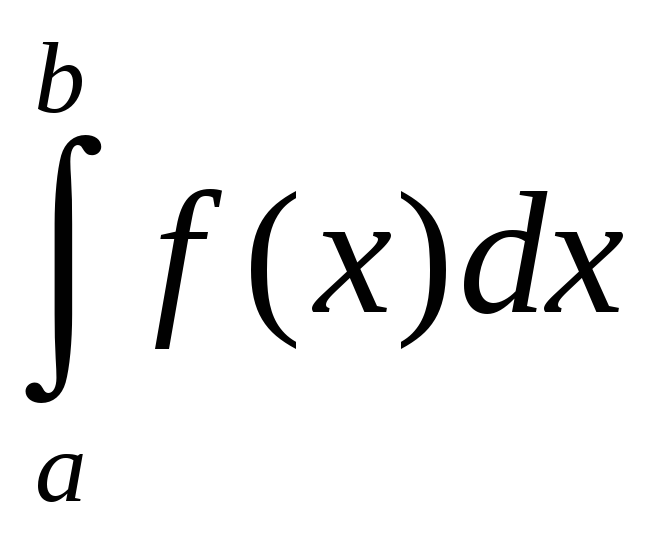 збежны
толькі пры
збежны
толькі пры
![]() .
.
Прыклад 1.
Даследуем
на збежнасць
![]() .
.
► Паколькі
![]() ,
то
,
то
![]() ,
а таму
,
а таму
![]() .
Такім чынам, інтэграл
.
Такім чынам, інтэграл
![]() разбежны, паколькі
разбежны, паколькі
![]() .
◄
.
◄
def.
НІ-2
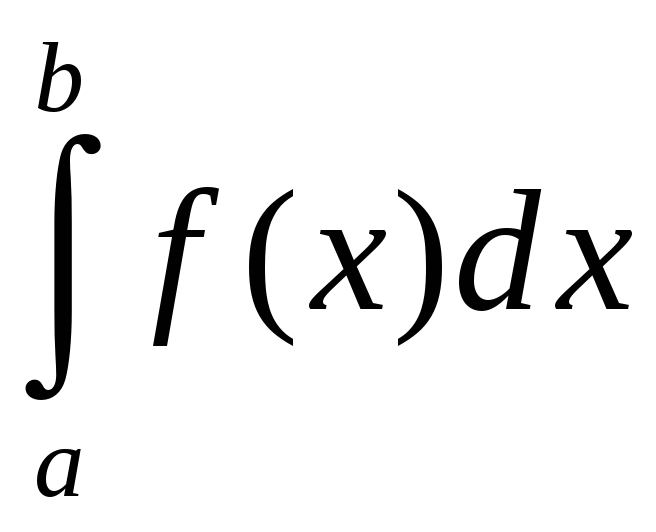 называецца
абсалютна
збежным,
калі збягаецца інтэграл
называецца
абсалютна
збежным,
калі збягаецца інтэграл
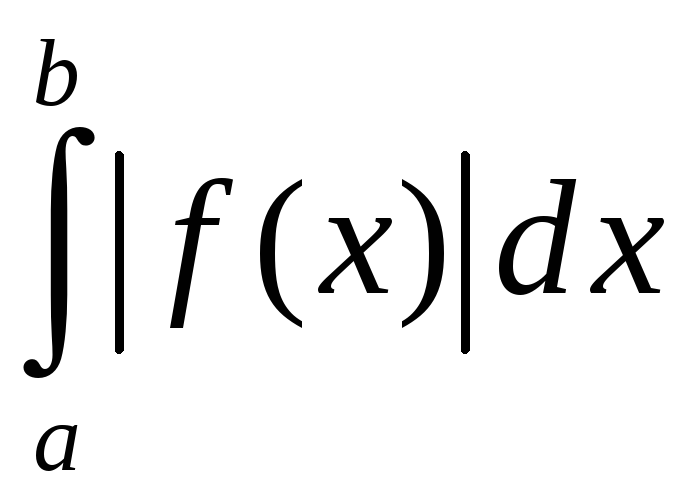 .
З
абсалютнай збежнасці інтэграла вынікае
яго збежнасць.
.
З
абсалютнай збежнасці інтэграла вынікае
яго збежнасць.
def.
Калі НІ-2
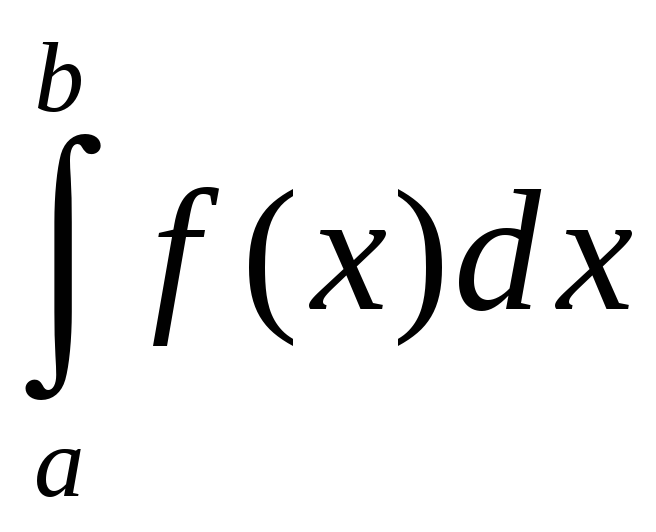 ёсць збежны, а інтэграл
ёсць збежны, а інтэграл
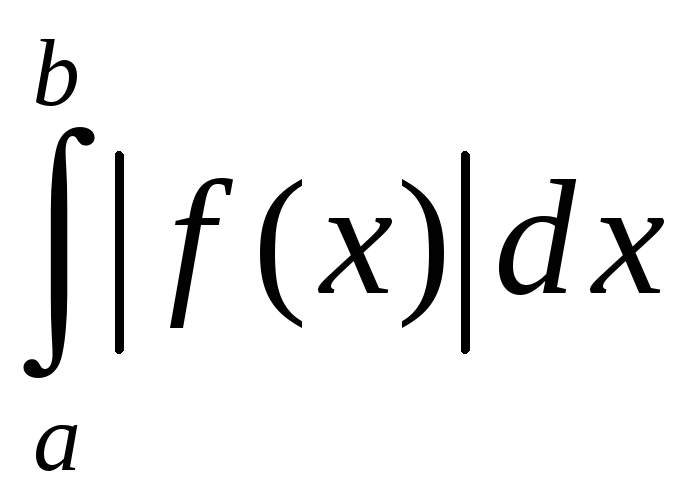 – разбежны то НІ-2 называецца ўмоўна
збежным.
– разбежны то НІ-2 называецца ўмоўна
збежным.
Прыклад 3.
Даследуем
на збежнасць інтэграл
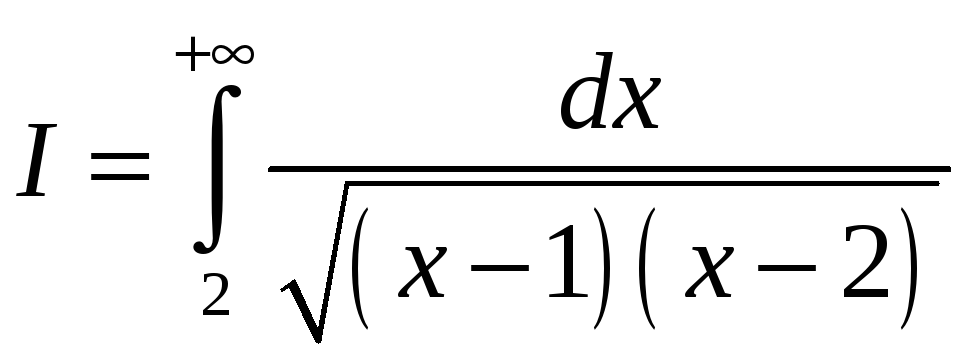 .
.
► Паколькі
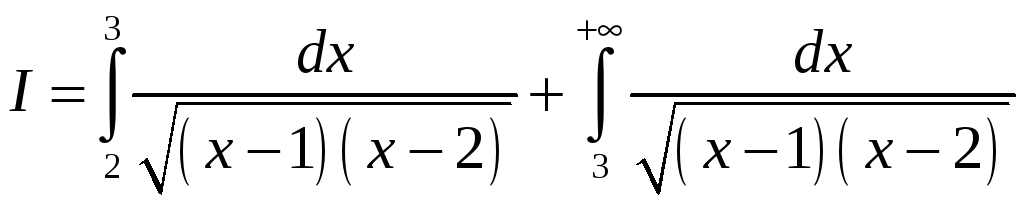 ,
то пабудуем для падынтэгральнай функцыі
эквівалентныя у пунктах
,
то пабудуем для падынтэгральнай функцыі
эквівалентныя у пунктах
![]() і
і
![]() :
:
1).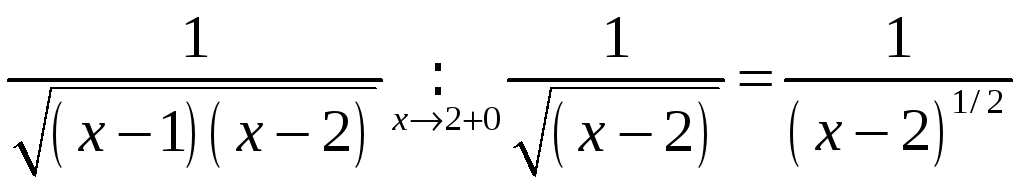 – інтэграл збежны;
– інтэграл збежны;
2). – інтэграл разбежны.
– інтэграл разбежны.
Такім
чынам, інтэграл
![]() ёсць разбежны. ◄
ёсць разбежны. ◄
Прыклад 4.
Даследуем
на збежнасць інтэграл
 .
.
► Паколькі
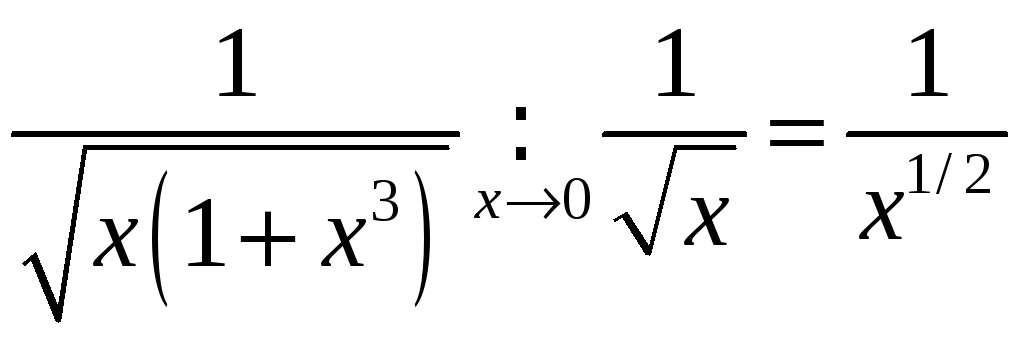 , то ў пункце
, то ў пункце
![]() інтэграл збежны, а паколькі
інтэграл збежны, а паколькі
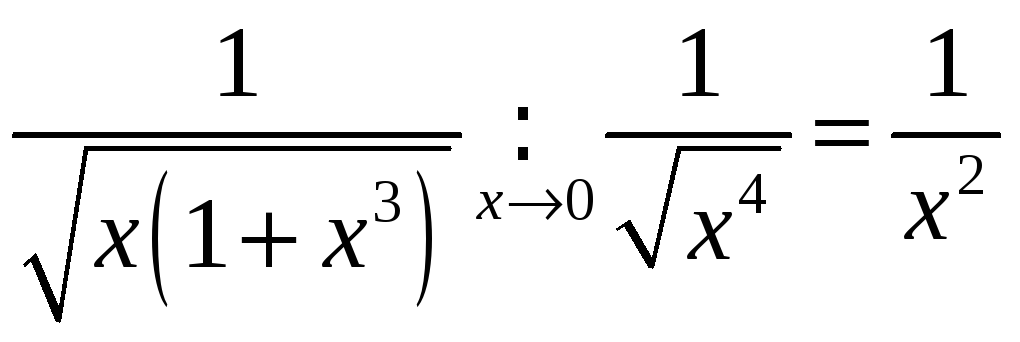 ,
то і ў пункце
,
то і ў пункце
![]() інтэграл збежны. Такім чынам, інтэграл
збежны. ◄
інтэграл збежны. Такім чынам, інтэграл
збежны. ◄
Прыклад 5.
Даследуем
на збежнасць інтэграл
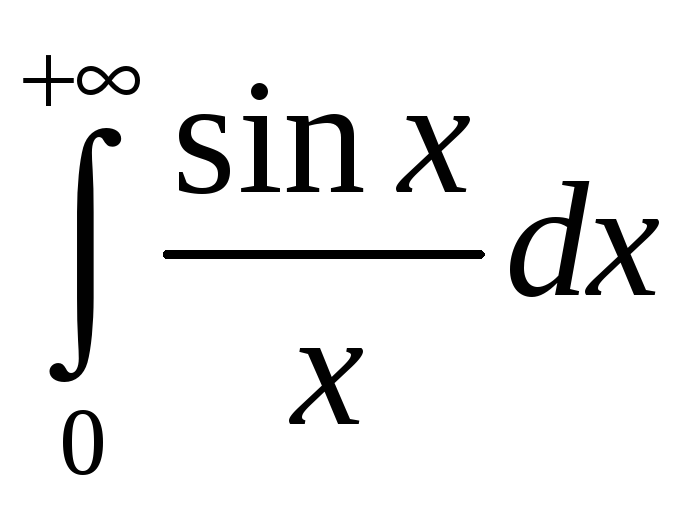 .
.
► Паколькі
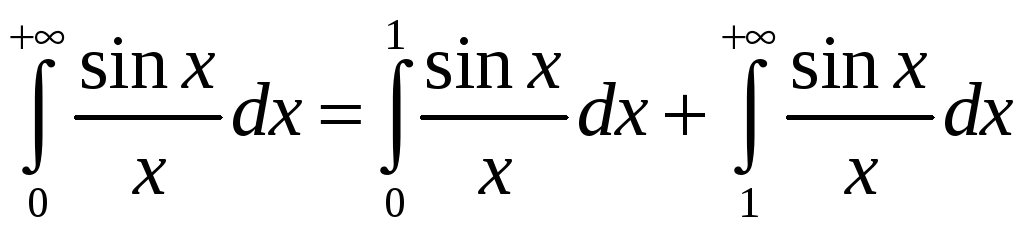 , то першы інтэграл існуе як вызначаны,
а другі ёсць збежны паводле прыкметы
Дырыхле. Такім чынам, інтэграл збежны.◄
, то першы інтэграл існуе як вызначаны,
а другі ёсць збежны паводле прыкметы
Дырыхле. Такім чынам, інтэграл збежны.◄
Прыклад 6.
Пры
якіх значэннях
![]() інтэграл
інтэграл
![]() ёсць збежны?
ёсць збежны?
► Заўсёды разбежны. ◄
