
- •Раздзел 4. Інтэгральнае злічэнне. §4.1. Азначэнне і ўласцівасці нявызначанага інтэграла.
- •1° Азначэнне нявызначанага інтэграла.
- •Тэарэма 1 (пра агульны выгляд першаіснай). Няхай функцыя ёсць першаісная для на х. Функцыя ёсць таксама першаісная для , калі і толькі калі .
- •2° Уласцівасці нявызначанага інтэграла.
- •§4.2. Асноўныя метады інтэгравання.
- •1º. Метад падстановы.
- •Тэарэма 1. Калі функцыя мае першаісную на прамежку т, а функцыя ёсць дыферэнцавальная на х, прычым , то
- •2º. Метад інтэгравання часткамі.
- •§4.4. Метад рацыяналізацыі.
- •1º. Інтэграванне дробава-лінейнай ірацыянальнасці.
- •2º. Інтэграванне біномнага дыферэнцыяла.
- •3º. Інтэграванне рацыянальна-трыганаметрычных функцый.
- •4º. Інтэграванне квадратовых ірацыянальнасцяў.
- •§4.5. Азначэнне і ўмовы існавання вызначанага інтэграла.
- •Прыклад 1. Вылічыць
- •Прыклад 2. Вылічыць паводле азначэння .
- •Заўвага. Абмежаванасць ёсць недастатковая ўмова для інтэгравальнасці функцыі.
- •Крытэр інтэгравальнасці. Для таго каб функцыя , вызначаная і абмежаваная на адрэзку , была інтэгравальнаю на гэтым адрэзку, неабходна і дастаткова, каб гэтая функцыя адпавядала ўмове
- •§4.6. Класы інтэгравальных функцый.
- •Тэарэма 1 (Інтэгравальнасць непарыўнай функцыі). Непарыўная на адрэзку функцыя ёсць інтэгравальная на гэтым адрэзку.
- •§4.8. Ацэнкі інтэгралаў.
- •Вынік 2 (Тэарэма пра пасярэдняе значэнне непарыўнай функцыі). Калі функцыя ёсць непарыўная, то існуе лік такі, што
- •1º. Формула Ньютана-Ляйбніца.
- •2º. Замена зменнай .
- •3º. Інтэграванне часткамі.
- •4º. Інтэграванне цотнай, няцотнай і перыядычнай функцый.
- •1º.Плошча плоскай фігуры.
- •Прыклад 1. Вылічыць плошчу фігуры, абмежаванай крывымі і .
- •Прыклад 2. Вылічыць плошчу фігуры, абмежаванай крывой . ►Спачатку зробім рысунак фігуры
- •2º. Даўжыня крывой.
- •Прыклад 3. Вылічыць даўжыню адной аркі цыклоіды (акружына радыюса коціцца па восі абцысаў).
- •3º. Аб’ём цела авароту.
- •Прыклад 5. Вылічыць аб’ём тора, г. Зн. Цела, якое атрымліваецца ад авароту круга радыюса вакол восі, што ляжыць у плоскасці гэтага круга на адлегласці ад яго цэнтра.
- •§4.13. Інтэграл па бясконцым прамежку (ні-1).
- •Прыклад 1. Вылічыць .
- •Тэарэма 2 (лімітавая прыкмета параўнання). Няхай функцыя а і няхай . Тады:
- •Калі ёсць збежны і , то – таксама збежны;
- •2) Калі ёсць разбежны і , то – разбежны.
- •Прыклады. А) збежны, бо .
- •§4.15. Умоўная збежнасць ні-1.
- •Тэарэма 1 (Прыкмета Дырыхле). Няхай функцыя ёсць непарыўная і мае абмежаваную першаісную на . Няхай функцыя ёсць непарыўна дыферэнцавальная і манатонная на і . Тады інтэграл – збежны.
- •Тэарэма 2 (прыкмета Абэля). Калі функцыя ёсць непарыўная на і – збежны, а функцыя абмежаваная і яе вытворная – непарыўная і не мяняе знаку на , то – збежны.
- •Прыклад 1. Даследаваць на абсалютную збежнасць інтэграл .
- •Прыклад 2. Даследуем інтэграл Фрэнэля на збежнасць.
- •§4.16. Неўласцівыя інтэгралы ад неабмежаваных функцый.
Тэарэма 1. Калі функцыя мае першаісную на прамежку т, а функцыя ёсць дыферэнцавальная на х, прычым , то
![]() (1)
(1)
□ Дастаткова
паказаць, што
![]() ёсць першаісная для падінтэгральнай
функцыі. Паводле правіла дыферэнцавання
складанай функцыі маем
ёсць першаісная для падінтэгральнай
функцыі. Паводле правіла дыферэнцавання
складанай функцыі маем
![]() .
■
.
■
Формулу (1) называюць формулай замены зменнай у нявызначаным інтэграле. Для яе практычнага выкарыстання больш зручным з’яўляецца наступны яе запіс
![]() (2)
(2)
прычым пры гэтым кажуць, што выкарыстоўваецца метад паднясення пад дыферэнцыял.
Такім чынам, у табліцы інтэгралаў зменную інтэгравання х можна разглядаць як функцыю ад іншай зменнай.
Прыклад 1.
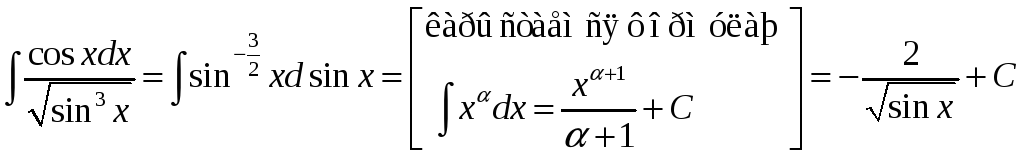 .
.
Прыклад 2.
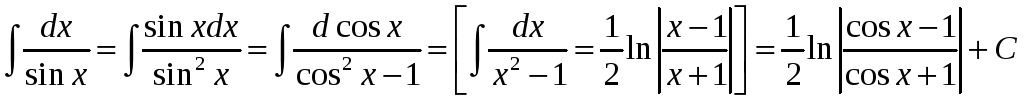 ,
,
або
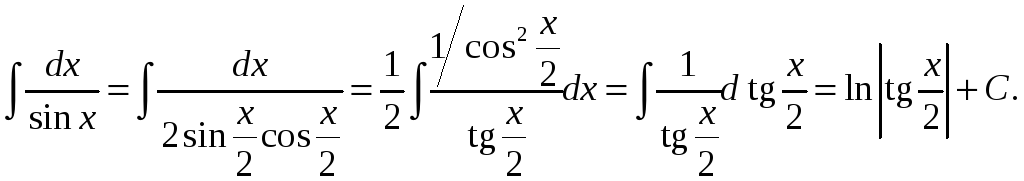
Прыклад 3.
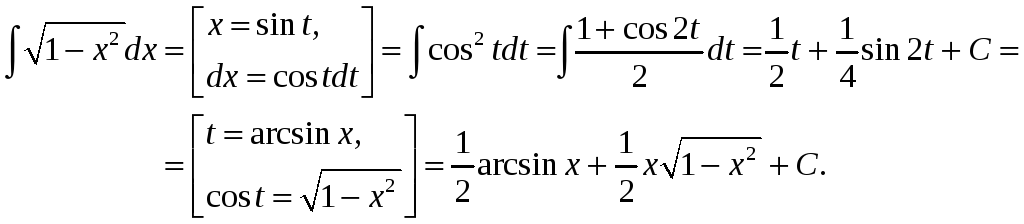
2º. Метад інтэгравання часткамі.
Тэарэма 2.
Калі
функцыі
![]() – дыферэнцавальныя на інтэрвале Х, а
функцыя
– дыферэнцавальныя на інтэрвале Х, а
функцыя
![]() мае
першаісную на гэтым інтэрвале, то функцыя
мае
першаісную на гэтым інтэрвале, то функцыя
![]() таксама мае на Х першаісную, прычым
таксама мае на Х першаісную, прычым
![]() .
(3)
.
(3)
□ Адпаведна
правілу дыферэнцавання здабытку маем
![]() ,
адкуль
,
адкуль
![]() .
Паколькі для функцыі
.
Паколькі для функцыі
![]() існуе першаісная, а для функцыі
існуе першаісная, а для функцыі
![]() першаіснай з’яўляецца
першаіснай з’яўляецца
![]() ,
то функцыя
,
то функцыя
![]() таксама мае першаісную, а таму
таксама мае першаісную, а таму

Канстанта
С
улучана ў нявызначаны інтэграл
![]() .
■
.
■
Формулу (3) звычайна выкарыстоўваюць у больш простым выглядзе
![]() (4)
(4)
Прыклад 4.
Вылічыць
![]() .
.
►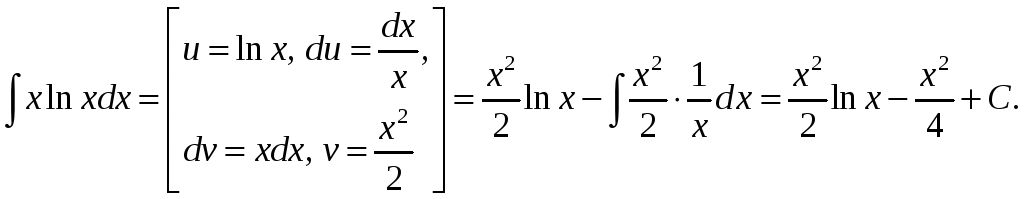 ◄
◄
Прыклад 5.
Вылічыць
![]()
►
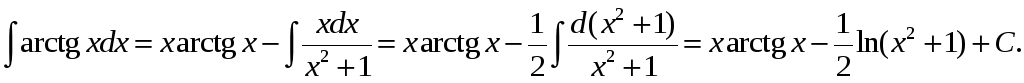 ◄
◄
Іншы раз інтэграванне часткамі даводзіцца выкарыстоўваць некалькі разоў.
Прыклад 6.
Вылічыць
![]() .
.
►
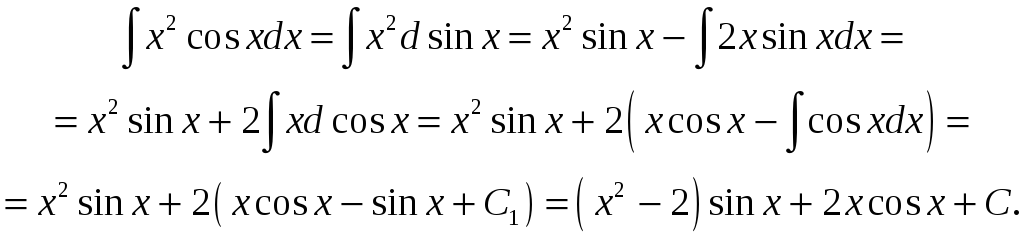 ◄
◄
Вылічэнне
інтэгралаў ад функцый
![]() зводзіцца да лінейнага раўнання ў
дачыненні да зыходнага інтэграла.
зводзіцца да лінейнага раўнання ў
дачыненні да зыходнага інтэграла.
Прыклад 7.
Вылічыць
![]() .
.
►
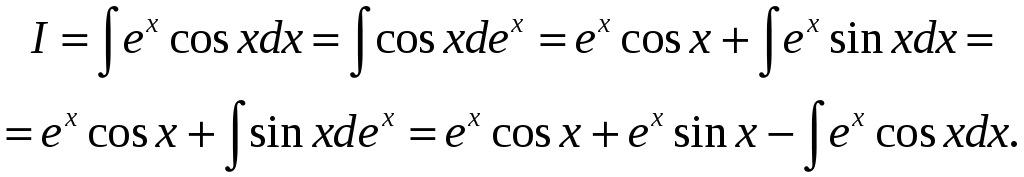
Прыйшлі
да раўнання
![]() ◄
◄
§4.3. Інтэграванне рацыянальных функцый.
Няхай
![]() – рацыянальная функцыя, дзе
– рацыянальная функцыя, дзе
![]() мнагасклады супеняў
мнагасклады супеняў
![]() і
і
![]() .
Калі
.
Калі
![]() (г. зн. рацыянальная функцыя ёсць
няправільная), то згодна з тэарэмаю пра
выяўленне мнагаскладу
(г. зн. рацыянальная функцыя ёсць
няправільная), то згодна з тэарэмаю пра
выяўленне мнагаскладу
![]() .
Такім чынам, маем
.
Такім чынам, маем
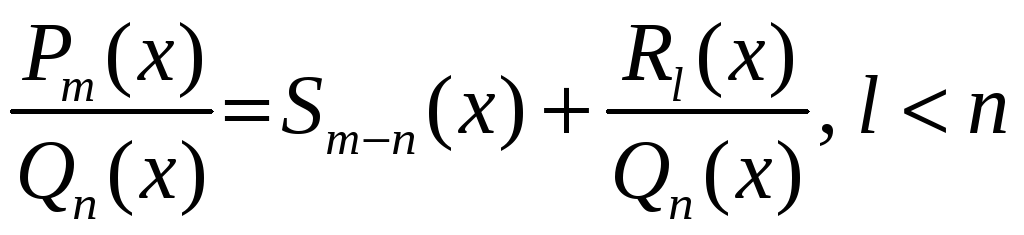 ,
г. зн. рацыянальную функцыю можна
падаць як суму мнагаскладу і правільнай
рацыянальнай функцыі. Мнагасклад
,
г. зн. рацыянальную функцыю можна
падаць як суму мнагаскладу і правільнай
рацыянальнай функцыі. Мнагасклад
![]() інтэгруецца як сума ступеневых функцый.
Што да правільнай рацыянальнай функцыі,
то згодна з тэарэмаю пра раскладанне
правільнай рацыянальнай функцыі на
суму простых дробаў, нам дастаткова
навучыцца інтэграваць простыя дробы:
інтэгруецца як сума ступеневых функцый.
Што да правільнай рацыянальнай функцыі,
то згодна з тэарэмаю пра раскладанне
правільнай рацыянальнай функцыі на
суму простых дробаў, нам дастаткова
навучыцца інтэграваць простыя дробы:
1)
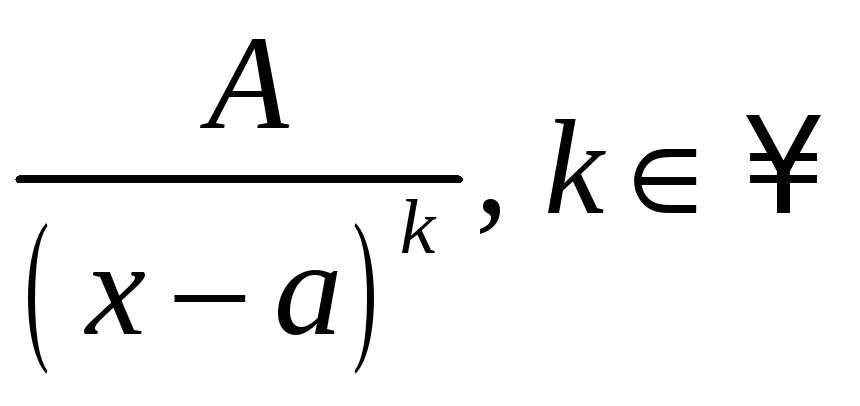 ;
2)
;
2)
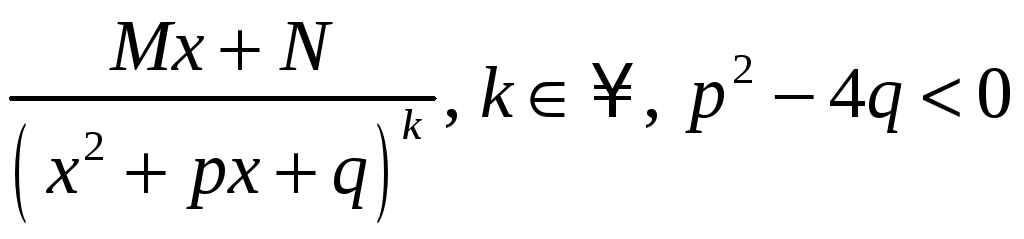 .
.
1а)
(![]() ).
).
![]() .
.
1б)
(![]() ).
).
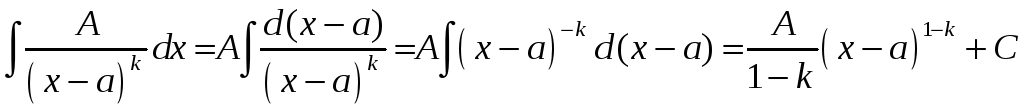 .
.
2)
У інтэграле
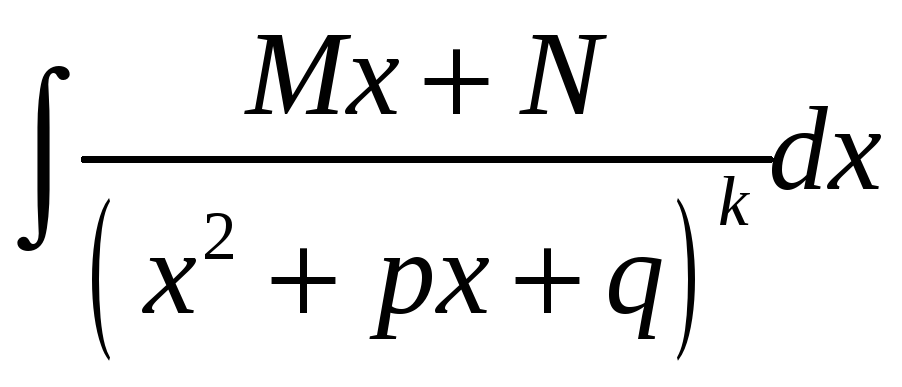 зробім замену зменнай
зробім замену зменнай
![]() ,
,
![]() .
Маем
.
Маем

А1)
![]()

А2)
![]()
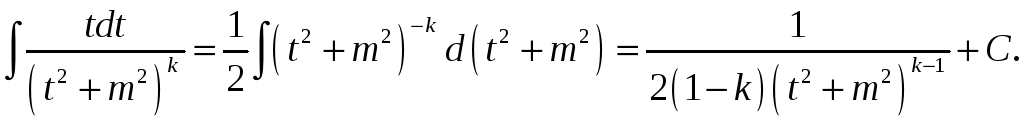
В1)
![]()
![]()
В2)
![]()
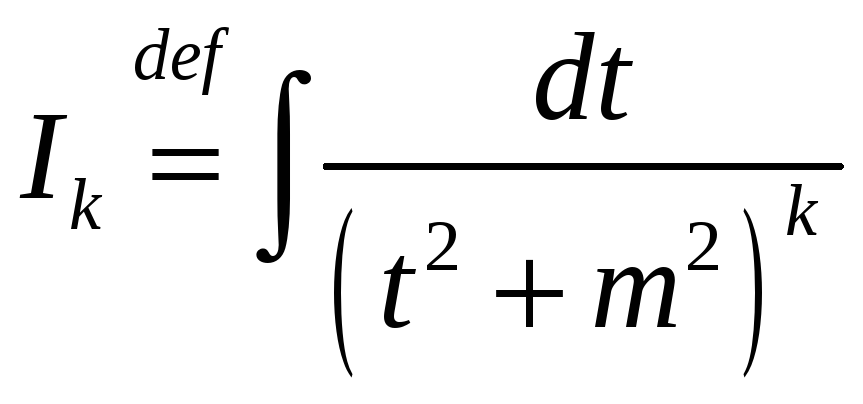 .
.
![]()
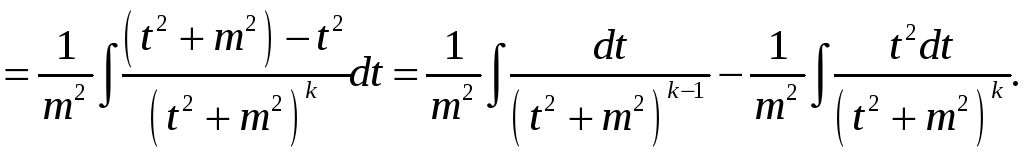 (1)
(1)
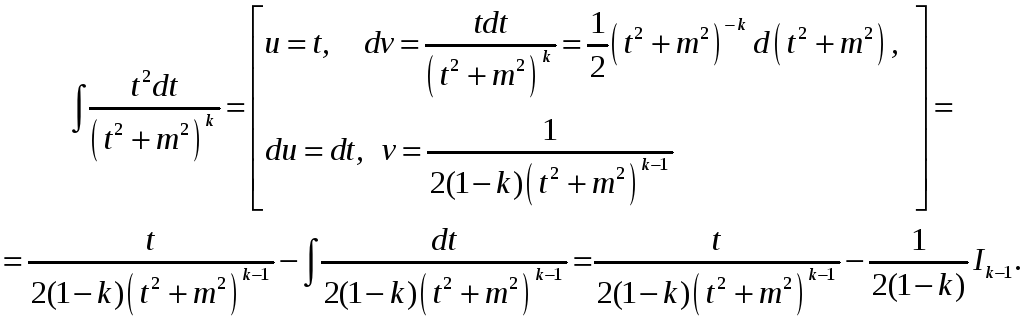 (2)
(2)
Падставім
(2) у (1)
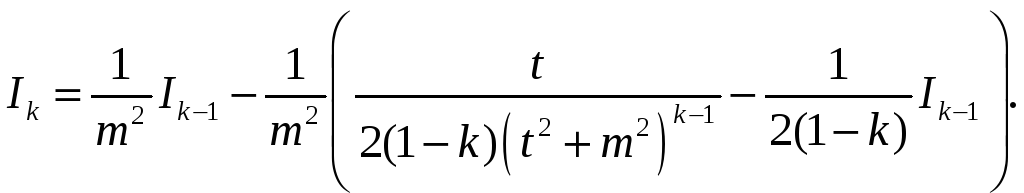
Адкуль
атрымліваем
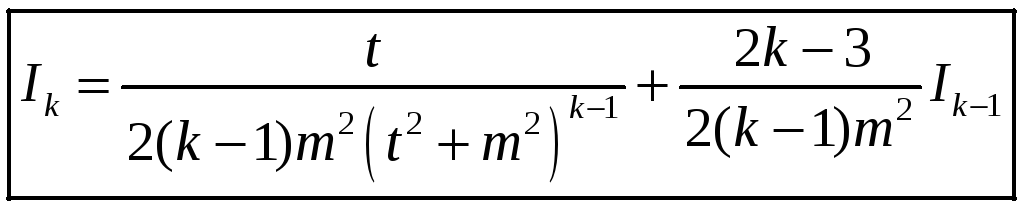 (3)
(3)
– рэкурэнтную
формулу для вылічэння інтэграла

Прыклад
1.
Вылічыць
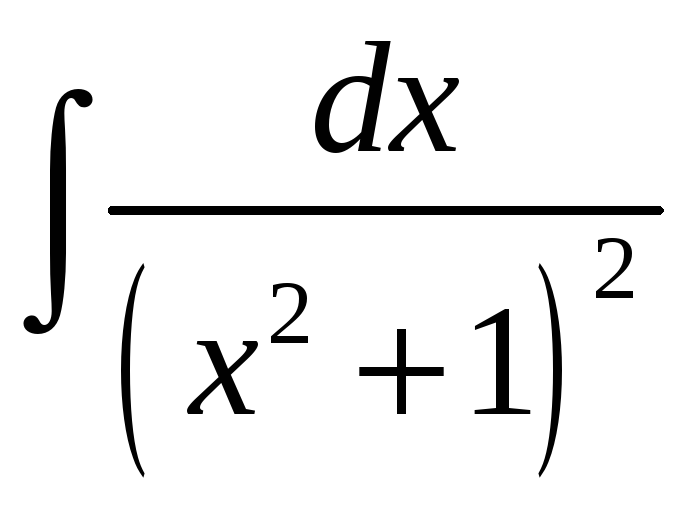 .
.
► Паводле формулы (3) маем
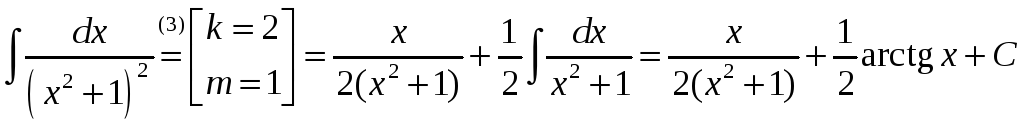 .
.
Прыклад
2.
Вылічыць
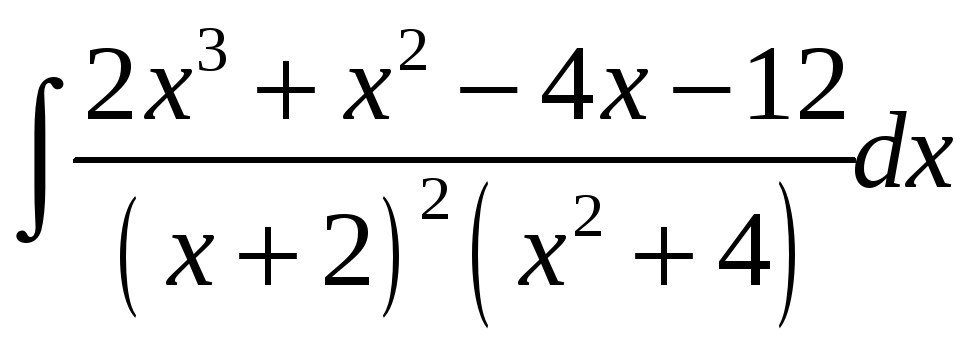 .
.
► Метадам нявызначаных каэфіцыентаў раскладзем падынтэгральную функцыю на суму простых дробаў
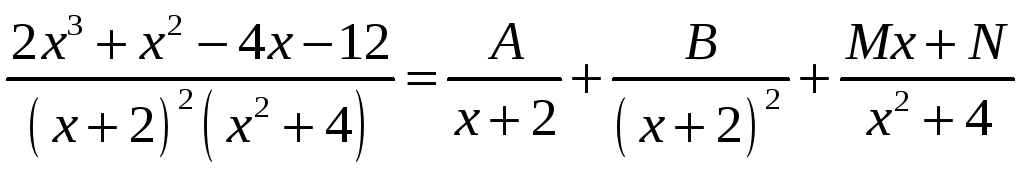 .
.
Спосабам
дамнажэння вылічаем канстанты
![]() :
:
![]() ,
,
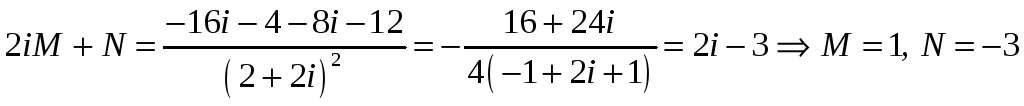 .
.
Пры
![]() маем
маем
![]() .
Такім чынам,
.
Такім чынам,
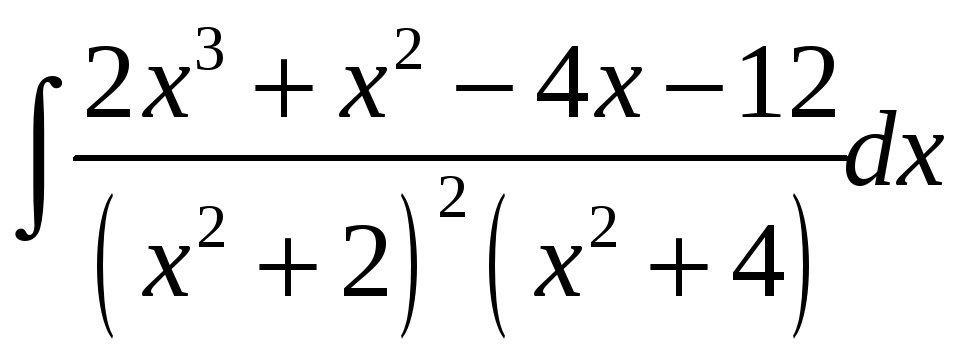 =
=
= .
◄
.
◄
Заўвага.
Калі назоўнік
![]() правільнай рацыянальнай функцыі
правільнай рацыянальнай функцыі
![]() мае кратныя корні, то пры вылічэнні
інтэграла карыстаюцца метадам
Астраградскага, паводле якога інтэграл
шукаецца ў выглядзе
мае кратныя корні, то пры вылічэнні
інтэграла карыстаюцца метадам
Астраградскага, паводле якога інтэграл
шукаецца ў выглядзе
 (4)
(4)
дзе
![]() – мнагасклад, які мае тыя ж корні, што
і мнагасклад
– мнагасклад, які мае тыя ж корні, што
і мнагасклад
![]() ,
але кратрасці 1, а
,
але кратрасці 1, а
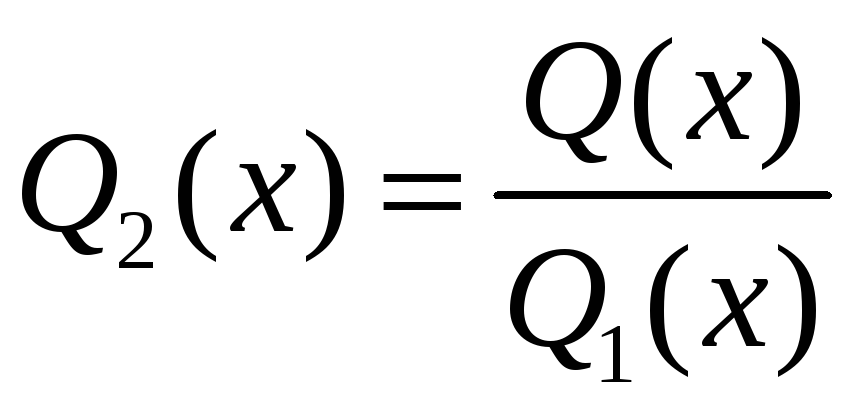 .
Пры гэтым функцыі
.
Пры гэтым функцыі
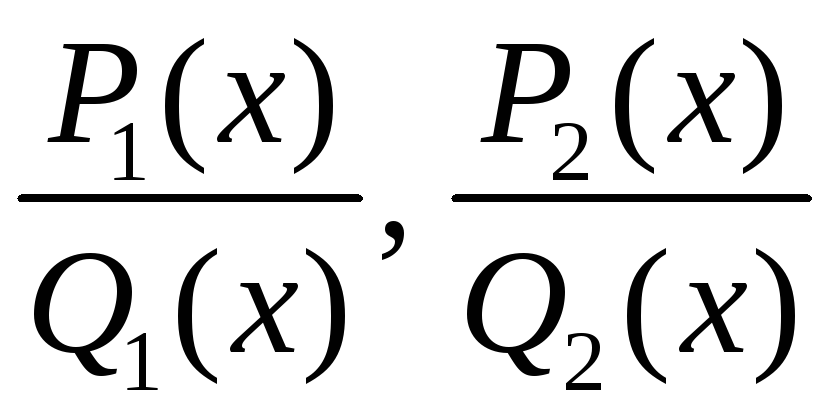 – правільныя рацыянальныя функцыі з
нявызначанымі ў лічніку каэфіцыентамі.
– правільныя рацыянальныя функцыі з
нявызначанымі ў лічніку каэфіцыентамі.
Каэфіцыенты
мнагаскладаў
![]() вылічаюцца метадам адпаведных каэфіцыентаў
з роўнасці, якая атрымліваецца пасля
дыферэнцавання (4).
вылічаюцца метадам адпаведных каэфіцыентаў
з роўнасці, якая атрымліваецца пасля
дыферэнцавання (4).
Прыклад
3.
Вылічыць
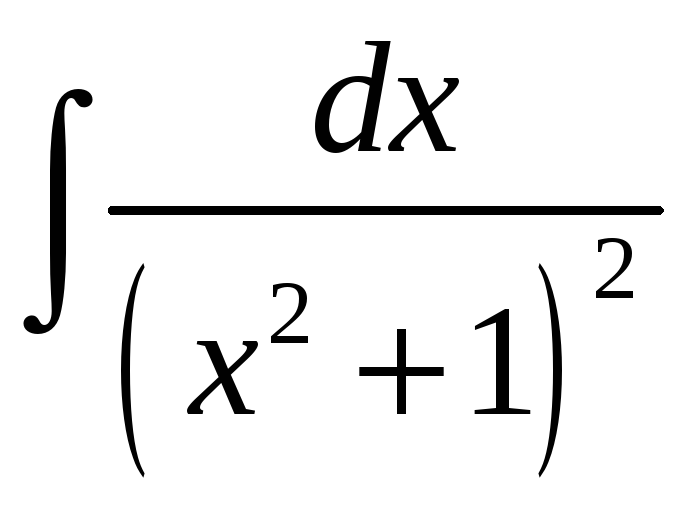 .
.
► Згодна з метадам Астраградскага запішам роўнасць
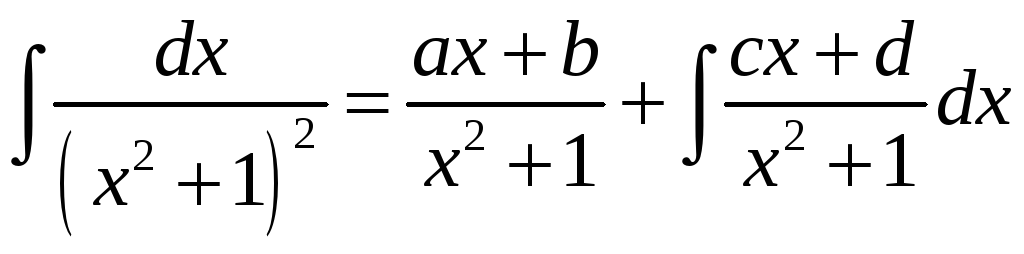 ,
пасля дыферэнцавання якой маем
,
пасля дыферэнцавання якой маем
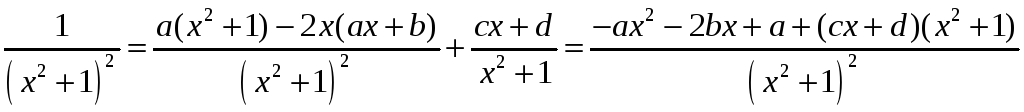 .
.
З апошняй роўнасці метадам адпаведных каэфіцыентаў атрымліваем сістэму
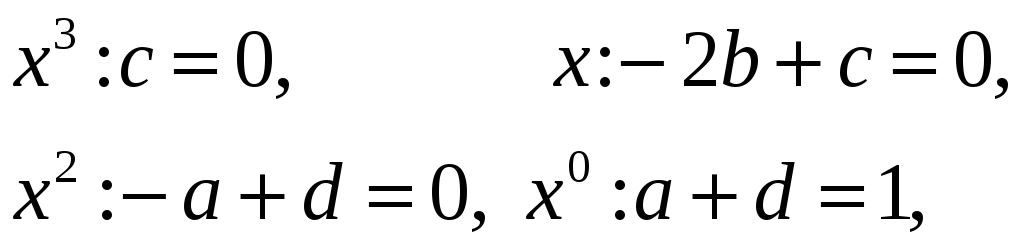
адкуль
![]() Такім чынам,
Такім чынам,
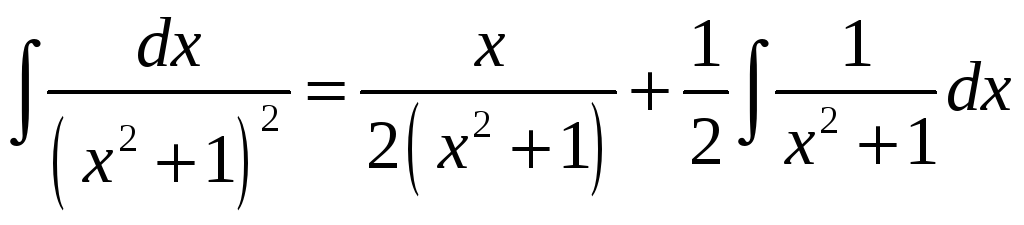 .
.
Канчаткова
маем
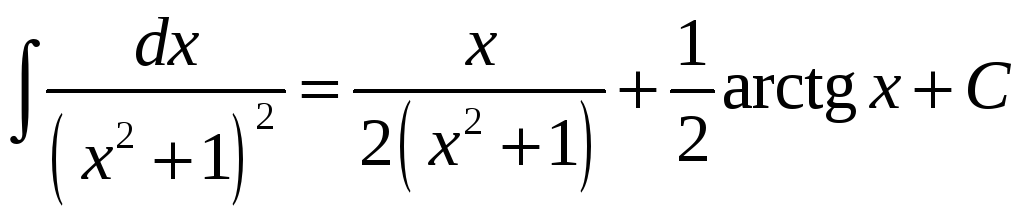 .
◄
.
◄
