§4.5. Азначэнне і ўмовы існавання вызначанага інтэграла.
Няхай
функцыя
вызначана на адрэзку
(магчыма разрыўная, магчыма непарыўная,
магчыма недыферэнцавальная, магчыма
дыферэнцавальная ў пунктах адрэзка).
Няхай
– сукупнасць пунктаў гэтага адрэзка
такіх, што
.
Мноства гэтых пунктаў назавем падзелам
адрэзка
і абазначым
.
Адрэзкі
назавем адрэзкамі
падзелу
,
або частковымі
адрэзкамі
адрэзка
.
Абазначым
праз
даўжыні адрэзкаў
.
Лік
назавем дробнасцю
падзелу
.
Мноства пунктаў
будзем называць выбаркай
з
адрэзка
.
Суму
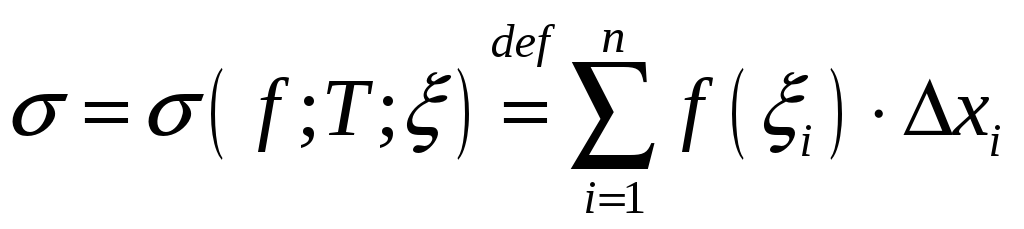будзем называць інтэгральнаю
сумай для
функцыі
пры зададзеным падзеле
і фіксаванай выбарцы
.
def.
Лік I
называюць вызначаным
інтэгралам
функцыі
на адрэзку
і абазначаюць
, калі
(1)
Пры
гэтым таксама кажуць, што існуе
ліміт
інтэгральных сумаў
пры
,
і гэты ліміт не залежыць ні ад падзелу
,
ні ад выбаркі
і пішуць
Калі
існуе лік
,
які вызначаецца ўмоваю (1), то функцыю
называюць інтэгравальнаю
паводле Рымана
на адрэзку
і пры гэтым кажуць таксама, што існуе
інтэграл
ад функцыі
на адрэзку
.
Такім чынам, функцыя ёсць інтэгравальная на адрэзку пры ўмове існавання ліміту інтэгральных сумаў, калі дробнасць падзелу адрэзка імкнецца да нуля, і гэты ліміт не залежыць ні ад падзелу, ні ад выбаркі.
Прыклад 1. Вылічыць
► Паколькі
,
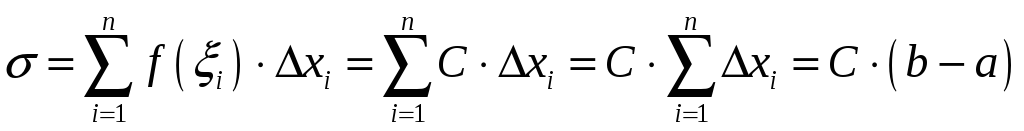то
,
а таму
.◄
|
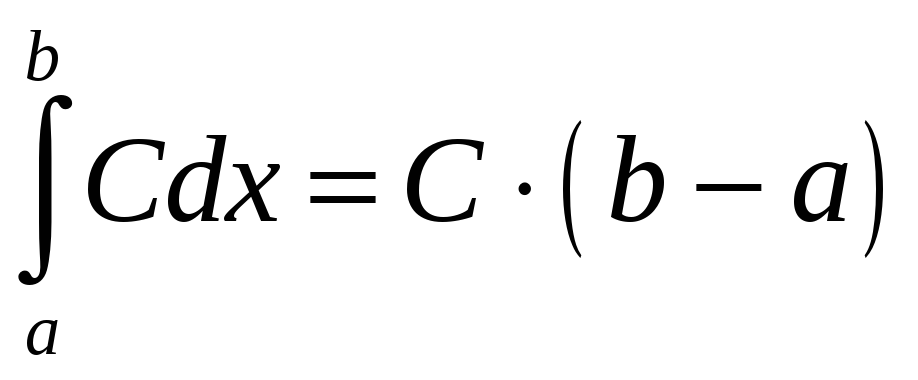Вызначаны
інітэграл мае просты геаметрычны
сэнс. Няхай
функцыя
|
|
ёсць неадмоўная і непарыўная на адрэзку
.
Тады інтэгральная сума
раўняецца плошчы “прыступкавай
фігуры” (гл. рысунак).
Фігуру
G
,
абмежаваную адрэзкамі прамых
і графікам функцыі
, г. зн.
,
будзем называць крывалінейнаю
трапецыяй.
Відавочна,
што пры дастаткова дробным падзеле
адрэзка
“прыступкавая фігура” мала чым
адрозніваецца ад крывалінейнай трапецыі,
а таму , калі функцыя
ёсць інтэгравальная на
,
то
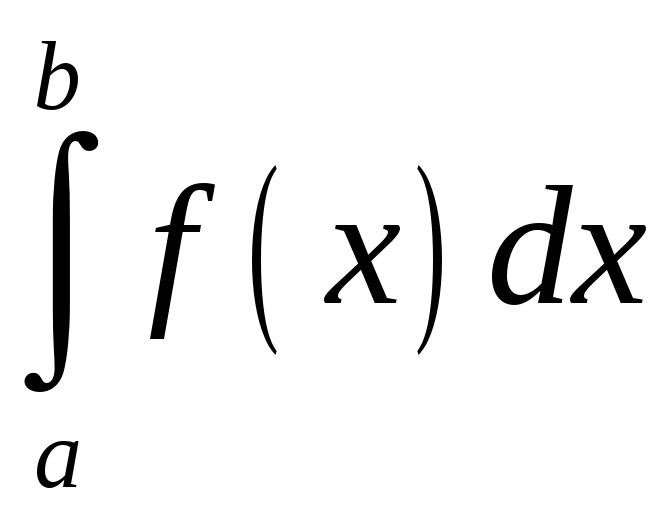азначае плошчу крывалінейнай трапецыі:
.
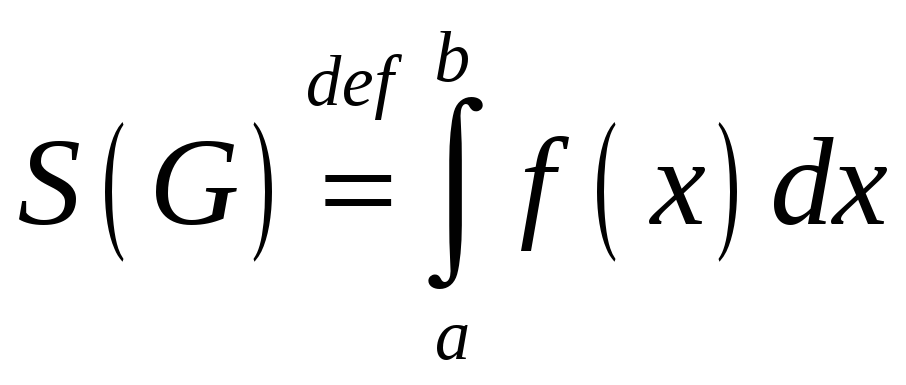Прыклад 2. Вылічыць паводле азначэння .
► Падзелім
адрэзак
на n
роўных (дзеля зручнасці) частак. Маем
,
а таму
,
калі
.
Выбіраючы
,
возьмем правыя канцы адрэзкаў
, г.зн.
.
Вылічым інтэгральную суму
.
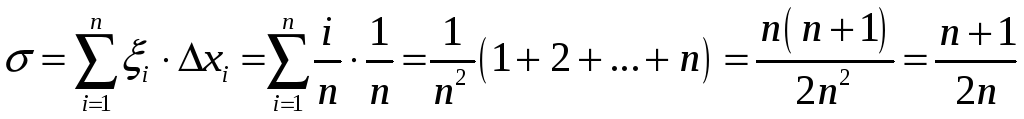Адкуль
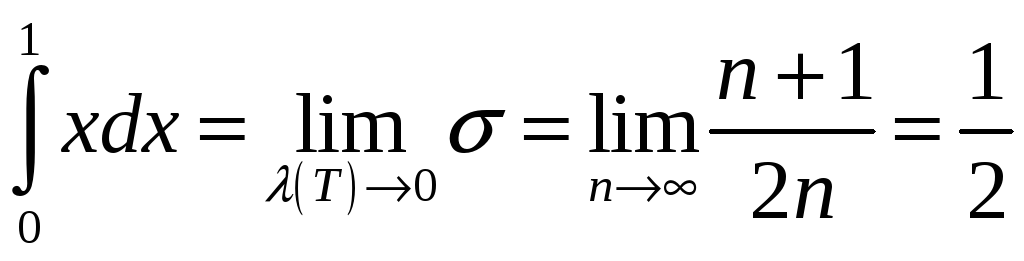. (Ці
з’яўляецца значэнне гэтага ліміта
значэннем адпаведнага інтэграла?)◄
Практыкаванне.
Пакажыце, што пры іншай выбарцы
, калі ўзяць у якасці
левыя канцы адрэзкаў
,
або іх сярэдзіны, то ліміт інтэгральных
сумаў будзе той жа самы.
Тэарэма 1
(неабходная
ўмова інтэгравальнасці функцыі).
Калі функцыя
ёсць інтэгравальная на адрэзку
,
то яна абмежаваная на гэтым адрэзку.
□ Паколькі
ёсць інтэгравальная на
то існуе лік I
, які адпавядае ўмове (1) , г.зн. пры
маем няроўнасць
,
(2)
якая
праўдзіцца пры кожным падзеле
і пры кожнай выбарцы
.
Зафіксуем
падзел
і дапусцім
процілеглае,
што функцыя
неабмежаваная на
.
Тады функцыя неабмежаваная прынамсі
на адным з адрэзкаў
падзелу
.
Не парушаючы агульнасці, будзем лічыць,
што
неабмежаваная на адрэзку
.
Зафіксуем пункты
і абазначым
.
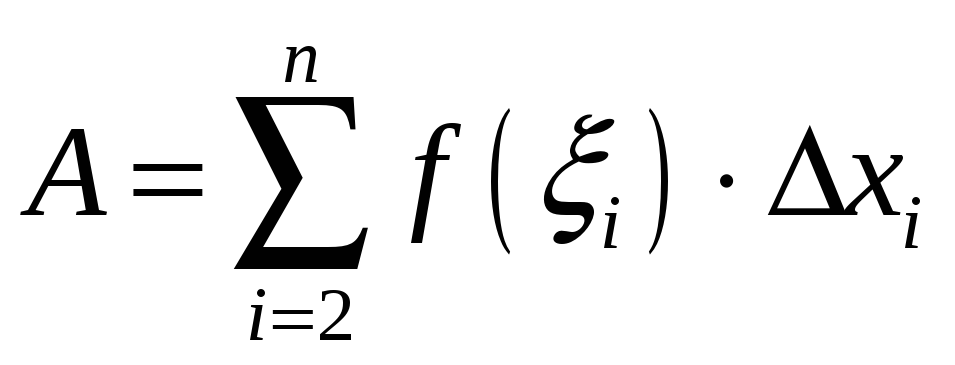Тады
і адпаведна няроўнасці (2), маем няроўнасць
,
якая праўдзіцца
.
Паколькі
,
то няроўнасць
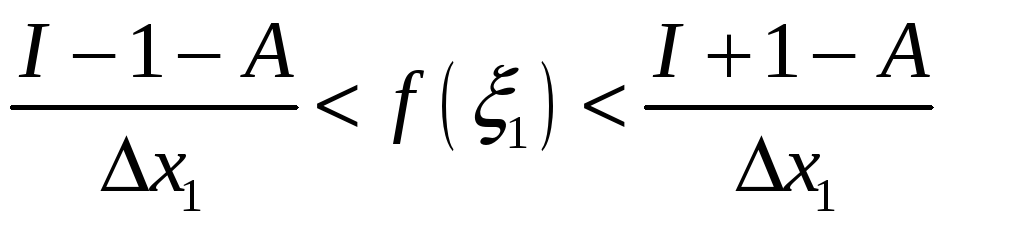праўдзівая
.
Гэта значыць, што функцыя
абмежаваная на адрэзку
,
што супярэчыць дапушчэнню неабмежаванасці
на
.
■