
- •Оглавление
- •Глава 1 интегрирование функций комплексного переменного
- •1.1. Основные понятия. Формы записи. Геометрическая интерпретация. Свойства
- •Теорема Коши для односвязной области
- •Теорема Морера
- •Теорема Коши для −связной области
- •Доказательство
- •Следствия теоремы Коши для −связной области
- •Интегральная формула Коши
- •Следствие интегральной формулы Коши
- •1.4. Задачи для самостоятельной работы (по главе 1)
- •Глава 2 Ряды в комплексной области.
- •2.1. Числовые ряды. Основные понятия
- •2.2. Функциональные ряды. Область сходимости. Равномерная сходимость. Свойства. Степенные ряды с комплексными членами
- •Свойства равномерно сходящихся рядов
- •Признак Вейерштрасса (достаточный признак равномерной сходимости)
- •Теорема Абеля
- •2.3. Ряды Тейлора Теорема
- •Основные разложения
- •2.4. Задачи для самостоятельной работы (по главе 2)
- •Библиографический список
- •Часть II
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение
высшего профессионального образования
ВЯТСКИЙ
ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет прикладной математики и телекоммуникаций
Кафедра прикладной математики и информатики
М.В. Хохлова
А.В. Черанева
Теория функций
комплексного переменного
Часть ΙI
Рекомендовано
Ученым советом
Вятского Государственного Университета
в качестве учебного пособия
Киров 2011
Печатается по решению редакционно-издательского совета Вятского государственного университета
УДК 621.865.8
Х 86
Рецензент: кандидат педагогических наук, доцент, заведующая кафедрой
математики Вятского социально-экономического института
А.И. Глушкова
Хохлова М.В. Теория функций комплексного переменного. Часть II: учебное пособие/М.В. Хохлова, А.В. Черанева.– Киров: Изд-во ВятГУ, 2011. – 73 с.
Учебное пособие для студентов технических специальностей дневной и заочной форм обучения, бакалавров по направлениям 210400, 210700, 220400, 230400, 221000, 230100, 010400 составлено в соответствии с программой по математике и включает основные разделы по теме «Теория функций комплексного переменного». Каждый раздел содержит необходимые теоретические сведения, комментированный набор задач, решение которых позволяет усвоить основные понятия по теории функций комплексного переменного. Пособие снабжено большим количеством задач для самостоятельной работы
Редактор Е.Г. Козвонина
Подписано в печать Усл.печ.л.
Бумага офсетная Печать
Заказ № Тираж Бесплатно.
Текст напечатан с оригинала-макета, представленного авторами.
__________________________________________________________
610000, г. Киров, ул. Московская, 36
Оформление обложки, изготовление – ПРИП ВятГУ
© Хохлова М.В., Черанева А.В., 2011
© Вятский государственный университет, 2011
Оглавление
ГЛАВА 1
интегрирование функций комплексного
переменного.………………..……………………………………............4
1.1. Основные понятия. Геометрическая интерпретация.
Формы записи. Свойства…………………………………………………4
1.2. Способы вычисления интегралов. Интеграл от аналитической
функции. Независимость интеграла от пути интегрирования.
Основные методы интегрирования. Формула Ньютона-Лейбница.........8
1.3. Интеграл по замкнутому контуру от аналитической функции.
Теорема Коши для
односвязной и для
![]() −связной
области.
−связной
области.
Интегральная формула Коши……………………………………………24
1.4. Задачи для самостоятельной работы (по главе 1)……………...…..37
Глава 2
Ряды в комплексной области……………………………….…....44
2.1. Числовые ряды. Основные понятия………………………………..44
2.2. Функциональные ряды. Область сходимости.
Равномерная сходимость. Свойства.
Степенные ряды с комплексными членами………………………..…...49
2.3. Ряды Тейлора………………………………………………………...58
2.4. Задачи для самостоятельной работы (по главе 2) …………………69
Библиографический список…………………………….…73
Глава 1 интегрирование функций комплексного переменного
1.1. Основные понятия. Формы записи. Геометрическая интерпретация. Свойства
кривая
![]() на плоскости задана параметрически
на плоскости задана параметрически
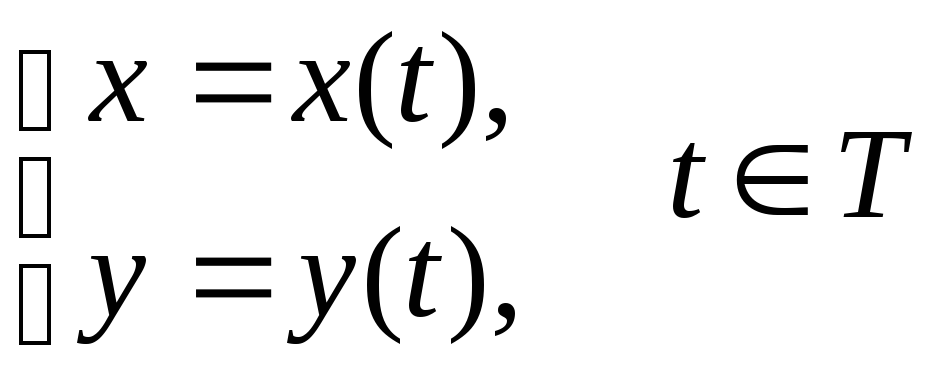 .
.
Если функции
![]() и
и
![]() имеют непрерывные производные
имеют непрерывные производные
![]() и
и
![]() ,
тогда эта кривая
является гладкой
на множестве
T.
,
тогда эта кривая
является гладкой
на множестве
T.
Гладкая кривая
геометрически характеризуется
существованием касательной к этой
кривой в каждой точке, если
![]() .
Направление касательной при движении
точки по гладкой кривой изменяется
непрерывно.
.
Направление касательной при движении
точки по гладкой кривой изменяется
непрерывно.

Рис. 1
Кривая является
кусочно-гладкой,
если ее можно разбить на конечное число
гладких кривых. Например, кривые
![]() и
и
![]() (см. рис. 1) являются гладкими на каждом
из интервалов
(см. рис. 1) являются гладкими на каждом
из интервалов
![]() и
и
![]() и кусочно-гладкими на общем интервале
и кусочно-гладкими на общем интервале
![]() .
.
Интеграл от функции
комплексного переменного
![]() ,
как и в действительной области, вводится
как предел
последовательности интегральных сумм.
,
как и в действительной области, вводится
как предел
последовательности интегральных сумм.
Задают однозначную
функцию
![]() , где
, где
![]() и
и
![]() − действительные функции переменных
− действительные функции переменных
![]() и
и
![]() .
Функция определена и непрерывна в
некоторой области
.
Функция определена и непрерывна в
некоторой области
![]() .
.
Выбирают
![]() – гладкую или кусочно-гладкую кривую,
целиком лежащую в области
– гладкую или кусочно-гладкую кривую,
целиком лежащую в области
![]() .
Кривая разбивается произвольным образом
на
.
Кривая разбивается произвольным образом
на
![]() частей
частей
![]() ,
,
![]() .
.
на кривой выбирают направление (начальная и конечная точка).
![]() − произвольная
точка, выбранная на дуге
− произвольная
точка, выбранная на дуге
![]() разбиения кривой.
разбиения кривой.
![]() − приращение
аргумента функции на этом участке
разбиения.
− приращение
аргумента функции на этом участке
разбиения.
![]() − длина хорды, соединяющей концы дуги
− длина хорды, соединяющей концы дуги
![]() .
.
Интегралом от
функции
![]() по кривой
по кривой
![]() называется предел интегральных сумм
называется предел интегральных сумм
 ,
(1)
,
(1)
если он существует и не зависит от способа разбиения и выбора произвольных точек.
Формула (1) определяет криволинейный интеграл от функции комплексного переменного. Интеграл обозначается как
![]() .
(2)
.
(2)
Для замкнутого
контура
![]() применяется следующее обозначение:
применяется следующее обозначение:
![]() .
(3)
.
(3)
Если в формулу
интеграла (2) подставить выражения для
функции
![]() и дифференциала
и дифференциала ![]() , то
вычисление
интеграла
от аналитической функции
, то
вычисление
интеграла
от аналитической функции
![]() комплексного переменного
комплексного переменного
![]() сводится к
вычислению двух криволинейных
интегралов по координатам
(криволинейных
интегралов II рода):
сводится к
вычислению двух криволинейных
интегралов по координатам
(криволинейных
интегралов II рода):
![]() .
(4)
.
(4)
Следовательно, свойства криволинейного интеграла от функций комплексного переменного аналогичны свойствам криволинейного интеграла II рода и известны из действительного анализа:
1. ![]() .
.
2. ![]() .
.
3. ![]() .
(5)
.
(5)
4. ![]() .
.
5. ![]() .
.
5*. Свойство
оценки модуля интеграла:
![]()
(если функция
ограничена по модулю
![]() на кривой Г).
на кривой Г).
Таким образом, формулу (4) можно рассматривать и как определение криволинейного интеграла от функции комплексного переменного, и как формулу его вычисления через криволинейные интегралы второго рода от функций двух действительных переменных.
Формулу легко использовать и запомнить, так как в левой части под знаком интеграла формально происходит выполнение следующих действий:
-
выделения действительной и мнимой части интегрируемой функции
 ,
, -
умножения на
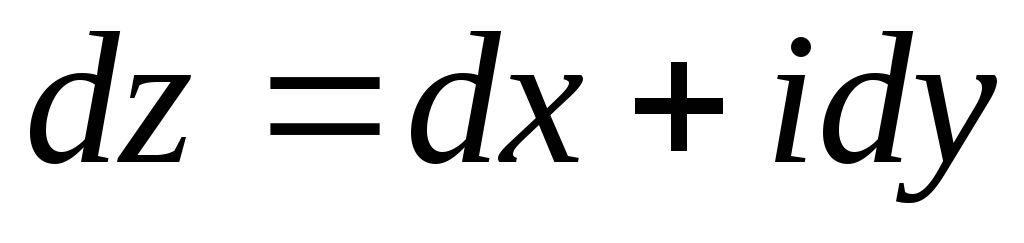 ,
, -
записи полученного выражения в алгебраической форме.
1.2. Способы вычисления интегралов.
Интеграл от аналитической функции.
Независимость интеграла от пути интегрирования.
Основные методы интегрирования.
Формула Ньютона-Лейбница
Способ вычисления интеграла зависит от способа задания кривой.
1) В случае
явного задания
кривой
![]() формула интегрирования (4) запишется в
виде
формула интегрирования (4) запишется в
виде
![]()
![]() .
(6)
.
(6)
2) Если кривая
Г
задана параметрическими
уравнениями в действительной
форме ![]() ,
где начальная и конечная точки дуги
соответствуют значениями
,
где начальная и конечная точки дуги
соответствуют значениями
![]() и
и
![]() ,
то, используя правила вычисления
интегралов второго рода, формулу
интегрирования (4) можно преобразовать
к виду
,
то, используя правила вычисления
интегралов второго рода, формулу
интегрирования (4) можно преобразовать
к виду
![]() (7)
(7)
![]()
![]()
![]() .
.
3) В случае
параметрического
задания
кривой непосредственно
![]() ,
формула (4) будет иметь вид
,
формула (4) будет иметь вид
![]() .
(8)
.
(8)
Отдельно следует
рассмотреть варианты параметризации
окружности
![]() с центром в точке
с центром в точке
![]() и радиусом
и радиусом
![]() :
:
![]()
![]()
![]() .
(9)
.
(9)
Параметризация в показательной форме имеет вид
![]() ,
,
![]() ,
, ![]() ,
, ![]() (10)
(10)
Особое внимание необходимо уделить случаю аналитичности подынтегральной функции. Для этого следует учесть ряд определений и свойств.
для
того чтобы функция ![]() ,
,
![]()
была дифференцируема
в точке z,
необходимо и достаточно, чтобы функции
![]() и
и
![]() были дифференцируемы в окрестности
точки
были дифференцируемы в окрестности
точки
![]() и удовлетворяли условиям
Коши-Римана:
и удовлетворяли условиям
Коши-Римана:
![]() и
и ![]() .
(11)
.
(11)
Выражение
![]() является
полным дифференциалом,
т.е.
является
полным дифференциалом,
т.е.
![]() ,
если выполняется условие (в односвязной
области):
,
если выполняется условие (в односвязной
области):
![]() .
(12)
.
(12)
Если
![]() − аналитическая
функция в
односвязной области
− аналитическая
функция в
односвязной области
![]() или подынтегральные выражения полученных
интегралов второго рода являются полными
дифференциалами, то интеграл
не зависит от пути интегрирования
(зависит
только от начальной и конечной точек).
или подынтегральные выражения полученных
интегралов второго рода являются полными
дифференциалами, то интеграл
не зависит от пути интегрирования
(зависит
только от начальной и конечной точек).
Первообразные аналитических функций в односвязных областях находят так же, как и в случае действительного анализа, используя свойства интегралов, таблицу интегралов и методы интегрирования.
для вычисления интеграла от аналитической функции (так как интеграл зависит только от начальной и конечной точек) применяется формула Ньютона-Лейбница:
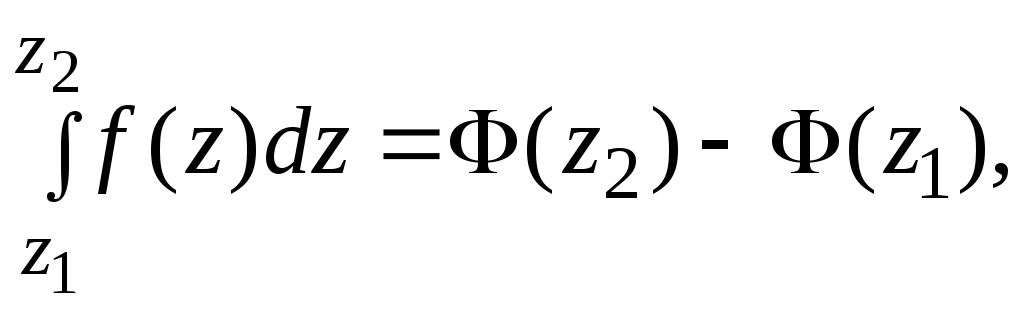 (13)
(13)
где
![]() − какая-либо первообразная для функции
− какая-либо первообразная для функции
![]() ,
т.е.
,
т.е.
![]() в области
в области
![]() ,
а
,
а
![]() и
и
![]() − начальная и конечная точки кривой.
− начальная и конечная точки кривой.
Если функции
![]() и
и
![]() аналитические в односвязной области
аналитические в односвязной области ![]() ,
а
,
а
![]() и
и
![]() − произвольные точки этой области, то
справедлива формула
интегрирования по частям:
− произвольные точки этой области, то
справедлива формула
интегрирования по частям:
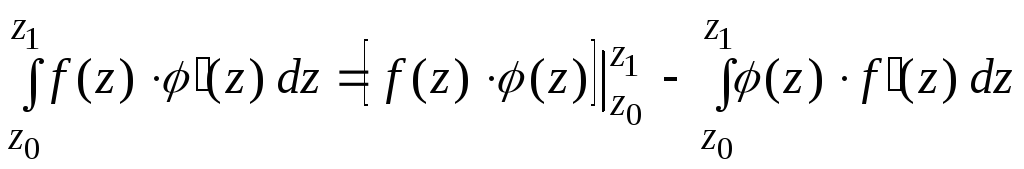 .
(14)
.
(14)
замена
переменных
в интегралах от функций комплексного
переменного производится аналогично
случаю функции действительного
переменного. При замене
![]() контур
контур
![]() на плоскости
на плоскости
![]() переходит в контур
переходит в контур
![]() на плоскости
на плоскости
![]() :
:
![]() .
(15)
.
(15)
Задача 1.
Вычислить
интеграл
![]() ,
,
где Г
− отрезок прямой от точки
![]() до точки
до точки
![]() .
.
Решение
Уравнение прямой
в данном случае имеет простой вид
![]() .
Взяв за параметр саму переменную
.
Взяв за параметр саму переменную
![]() ,
получают
,
получают
![]() .
При данных условиях переменная
.
При данных условиях переменная
![]() изменяется от
изменяется от
![]() до
до
![]() .
.
Подынтегральная функция имеет вид
![]()
![]() .
.
после
замены
![]() получают действительную часть функции
получают действительную часть функции
![]() и мнимую часть
и мнимую часть
![]() .
.
Подынтегральное
выражение сводят к одной переменной
![]() ,
используя формулу (6):
,
используя формулу (6):
![]() =
=
![]() =
=
![]()
=![]()
![]() .
.
Задача 2.
Вычислить интеграл
![]() по следующим кривым:
по следующим кривым:
1) по отрезку AB:
A ![]() ,
B (
,
B (![]() );
);
2) по верхней
полуокружности
![]() ,
начало пути в точке
,
начало пути в точке
![]() ;
;
3) по окружности
![]() ,
начало пути в точке
,
начало пути в точке
![]() .
.
Решение
1) составляют
уравнение прямой по формуле
![]() .
.
Подставляют
значения координат
![]() .
.
Тогда ![]() или
или
![]() .
.
Уравнение прямой
![]() можно получить и координатным методом:
угловой коэффициент
можно получить и координатным методом:
угловой коэффициент
![]()
![]() или
или
![]() .
.
Далее преобразуют подынтегральное выражение:
![]() ,
,
![]()
![]() .
.
Переменную
интегрирования в каждом из криволинейных
интегралов можно оставить свою, так как
на заданной прямой
![]() и
и
![]() .
.
Координаты точек
A ![]() ,
B (
,
B (![]() )
позволяют раскрыть модульные выражения:
)
позволяют раскрыть модульные выражения:![]()
![]()
![]() ,
,
![]()
![]()
![]() .
.
![]() =
= =
=
![]()
![]()
![]() .
.
2) Кривая
![]() в переменных
в переменных
![]() имеет вид
имеет вид
![]() или
или
![]() .
.
Это окружность с
центром в точке
![]() и радиусом
и радиусом
![]() .
.
Вводят параметризацию кривой по формулам (9):
![]() .
.
Для верхней
полуокружности (см. рис. 2)
![]() .
.
![]() .
.
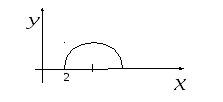
Рис. 2
Используя формулу (7), получают
![]()
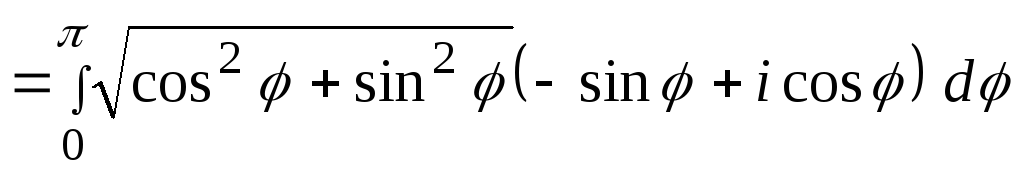
![]() .
.
Если окружность задать в показательной форме (10), то можно вычислить и по-другому:
![]() ,
, ![]() ,
, ![]() .
.
![]()
![]()
3) Уравнение
![]() в переменных
в переменных
![]() представляет собой окружность
представляет собой окружность
![]() радиуса
радиуса
![]() (см рис. 3).
(см рис. 3).
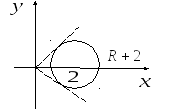
Рис. 3
Вводят параметризацию окружности:
![]() ,
, ![]() .
.
![]()
=![]() .
.
Этот способ вычисления можно сравнить с вариантом вычисления интеграла для переменной в показательной форме:
![]() ,
, ![]() ,
, ![]() .
.
![]() .
.
В вычислениях
можно сразу использовать свойство
периодичности
![]() для функции
для функции
![]() ,
следовательно,
,
следовательно,
![]() ,
или формулу Эйлера
,
или формулу Эйлера
![]() :
:
![]()
Задача 3.
Вычислить интеграл
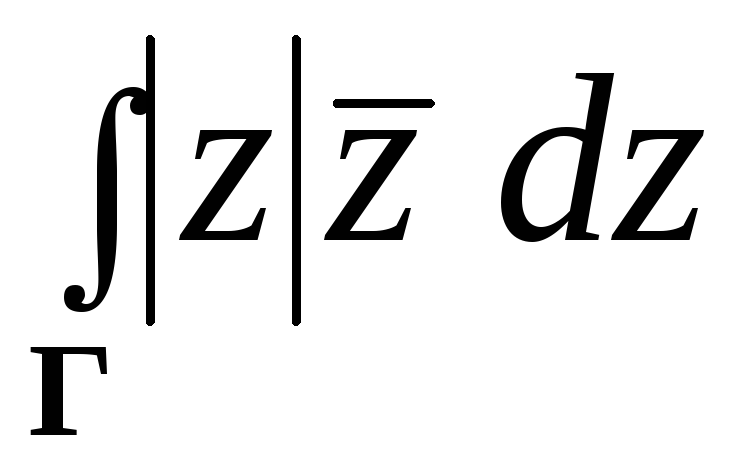 по замкнутому
контуру,
по замкнутому
контуру,
который состоит
из верхней полуокружности
![]() и отрезка прямой
и отрезка прямой
![]() ,
,
![]() (начало пути в точке
(начало пути в точке
![]() ).
).
Решение
Замкнутый контур Г состоит из двух различных участков: отрезка прямой АОВ и верхней полуокружности ВСА. Вычисление начинают с преобразования подынтегрального выражения.
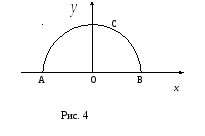
Для участка АОВ
(см. рис. 4):
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Переменная
интегрирования
![]() .
.
![]() .
.
Для участка ВСА
(верхняя
полуокружность):
![]()
![]() .
.
![]() .
.
Тогда ![]() .
.
Общий результат: ![]() .
.
Задача 4.
Вычислить интеграл
![]() .
.
Решение
Преобразуют подынтегральную функцию, выделяя действительную и мнимую часть:
![]()
![]() ,
т.е.
,
т.е.
![]() ,
, ![]() .
.
Проверяют выполнение условий Коши-Римана (11):
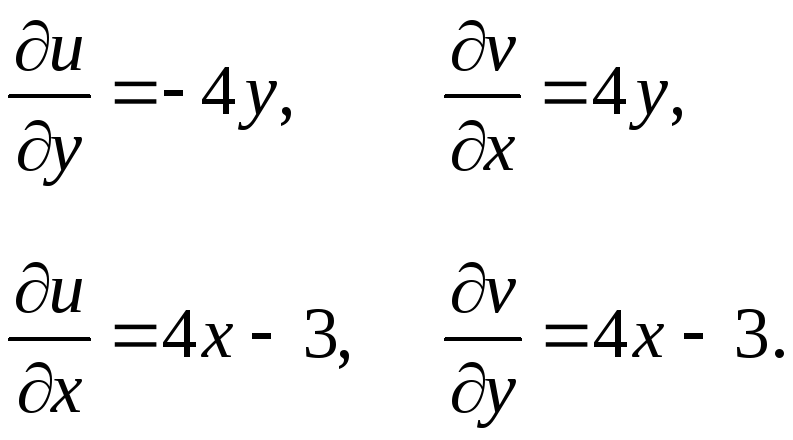
![]() .
.
Условия выполняются.
Подынтегральная функция
![]() является аналитической функцией на
всей комплексной плоскости.
является аналитической функцией на
всей комплексной плоскости.
По формуле Ньютона-Лейбница (13) находят:
![]()
![]()
![]()
![]()
![]()
Задача 5.
Вычислить интеграл
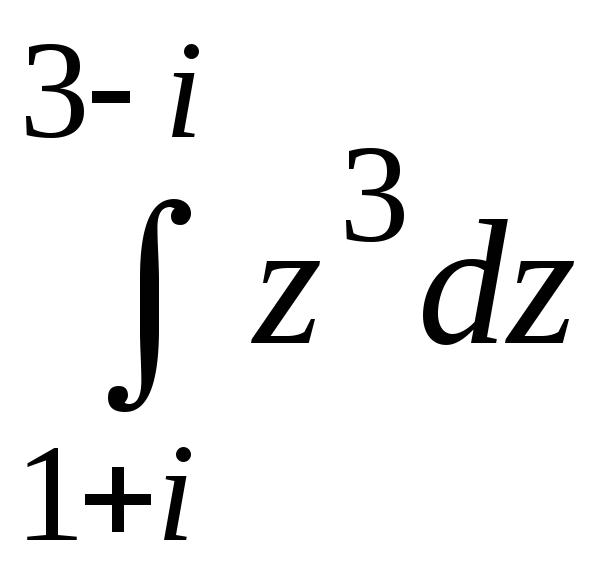 .
.
Решение
Функция
![]() является аналитической на всей комплексной
плоскости (проверить
самостоятельно).
является аналитической на всей комплексной
плоскости (проверить
самостоятельно).
По формуле Ньютона-Лейбница (13) находят:
![]() .
.
Задача 6.
Вычислить интеграл
![]() по
замкнутому контуру
по
замкнутому контуру
![]() при условии
при условии
![]() .
.
Решение
Функция
![]() является
является
неоднозначной.
Делают разрез по лучу
![]() .
В соответствии с заданным условием
выбирают однозначную ветвь функции
.
В соответствии с заданным условием
выбирают однозначную ветвь функции
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() и
и
![]() .
.
Обозначают ![]() .
.
Тогда на единичной
окружности подынтегральная функция
принимает вид ![]() .
.
Вычисляют интеграл методом интегрирования по частям (14):
![]()
= ![]() .
.
Задача 7. Н айти
айти
![]() ,
,
где Г
− правая часть окружности:
![]() .
.
Решение
![]() .
.
Для правой части окружности (см. рис. 5):
![]() ,
,
![]() ,
,
![]() .
.
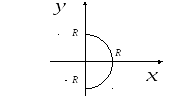
Рис. 5
Лучше сразу ввести
параметризацию для
![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
![]()
![]()
=![]()
![]() .
.
Задача 8.
Исследовать
значение интеграла ![]()
от
параметра
![]() ,
где Г
−
круг радиуса
,
где Г
−
круг радиуса
![]() с центром в точке
с центром в точке
![]() .
.
Решение
Для окружности со смещенным центром по формулам (10)
![]() ,
,
![]() ,
, ![]() .
.
Если
![]() ,
то
,
то ![]() .
.
Если
![]() ,
то
,
то
![]()
![]() .
.
(Период функции
![]() равен
равен
![]() .)
.)
Окончательно
получают ![]()
Задача 9.
Исследовать
значение интеграла ![]()
по различным
траекториям
![]() от точки
от точки
![]() до точки
до точки
![]()
(вдоль прямой; вдоль ломаной со сторонами параллельно осям координат; по верхней полуокружности).
Решение
Преобразуют
функцию
![]() :
:
![]()
![]()
![]() .
.
Выделяют действительную и мнимую части
![]()
![]() ,
,
![]()
![]() .
.
Проверяют
условия
Коши-Римана ![]() и
и ![]() следующим образом:
следующим образом:
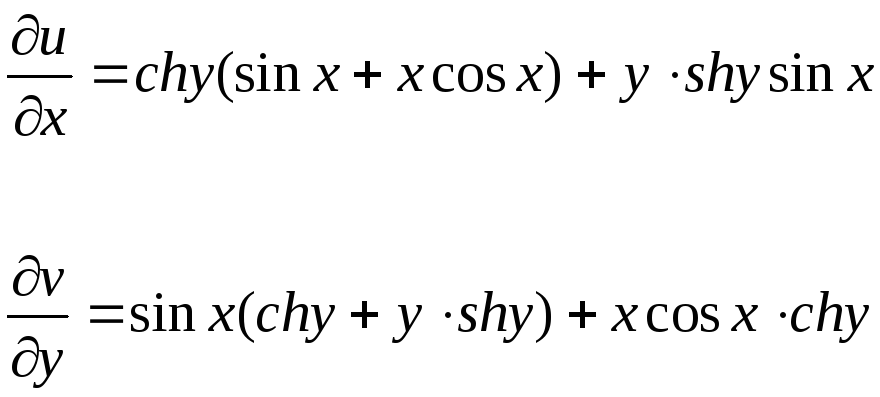
![]()
![]()
![]() ,
,
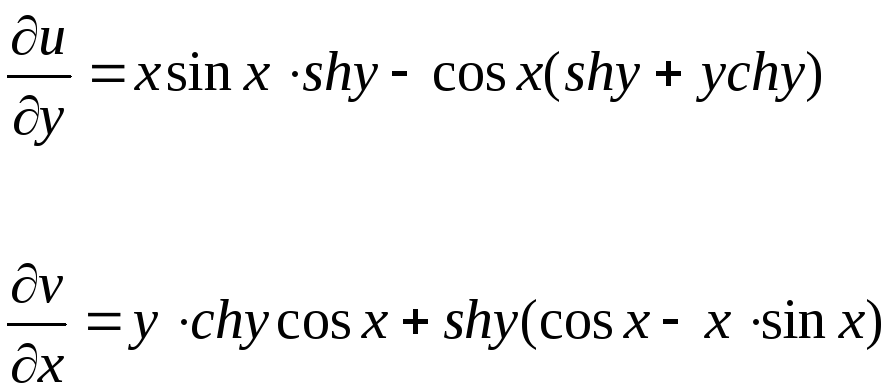
![]()
![]() .
.
Условия Коши-Римана
выполняются. Функция
![]() является аналитической на всей комплексной
плоскости, следовательно, данный интеграл
не зависит от выбора пути интегрирования
является аналитической на всей комплексной
плоскости, следовательно, данный интеграл
не зависит от выбора пути интегрирования
![]() .
.
Для вычисления интеграла применяют метод интегрирования по частям и формулу Ньютона-Лейбница:
 ,
,
![]()

![]() .
.
1.3. Интеграл по замкнутому контуру
от аналитической функции.
Теорема
Коши для односвязной и для
![]() −связной
области.
−связной
области.
Интегральная формула Коши
При исследовании поведения функций в ограниченных областях или в окрестностях отдельных точек в различных приложениях интегрального исчисления функций комплексного переменного рассматриваются интегралы по замкнутым кривым – границам областей, в частности окрестности точек.
Пусть
![]() непрерывная однозначная аналитическая
функция. Для нее выполняются условия
Коши-Римана (11):
непрерывная однозначная аналитическая
функция. Для нее выполняются условия
Коши-Римана (11):
![]() ,
,
![]() .
.
Известно, что ![]() ,
если выполняется условие (12):
,
если выполняется условие (12):
![]() .
.
Исследуют
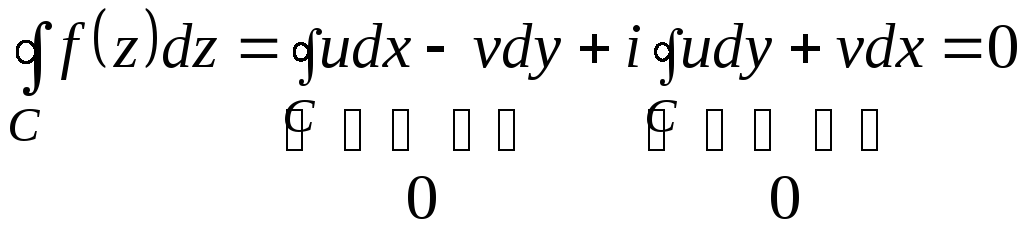 .
.
Получают аналогичные условия
![]() ,
, ![]() .
.
Полученные условия
совпадают с условиями Коши-Римана,
которые выполняются для функции
![]() в силу предположения о том, что функция
является аналитической.
в силу предположения о том, что функция
является аналитической.
