
- •Федеральное агентство связи
- •Московский технический университет связи и информатики
- •Конспект лекций по обыкновенным дифференциальным уравнениям. Ч.3.
- •1. Понятие об устойчивости решений дифференциальных уравнений.
- •1.1. Простейшие типы точек покоя.
- •1.2. Замечания по поводу классификации точек покоя.
- •1.3. Однородная система линейных уравнений с постоянными коэффициентами.
- •2. Теоремы Ляпунова об устойчивости.
- •3. Исследование на устойчивость по первому приближению.
- •4. Дифференциальные уравнения с частными производными первого порядка
- •4.1. Первые интегралы систем дифференциальных уравнений
- •4.2. Характеристики
- •5. Линейные однородные дифференциальные уравнения в частных производных первого порядка с независимыми переменными.
- •6. Дифференциальные уравнения, допускающие понижение порядка.
- •Конспект лекций по обыкновенным дифференциальным уравнениям. Ч.3.
1.1. Простейшие типы точек покоя.
Исследуем расположение траекторий в окрестности точки покоя x=0, y=0 системы двух линейных однородных дифференциальных уравнений с постоянными коэффициентами.
 (6)
(6)
где
![]()
Решение ищем
в виде
![]() .
Тогда имеем характеристическое уравнение
.
Тогда имеем характеристическое уравнение
![]()
т.е.
![]()
а
![]() и
и
![]() с точностью до постоянного множителя
определяются из одного из уравнений
с точностью до постоянного множителя
определяются из одного из уравнений
![]() (7)
(7)
Рассмотрим следующие случаи.
а) Корни
характеристического уравнения
![]() и
и
![]() действительны и различны.
действительны и различны.
Общее решение имеет вид
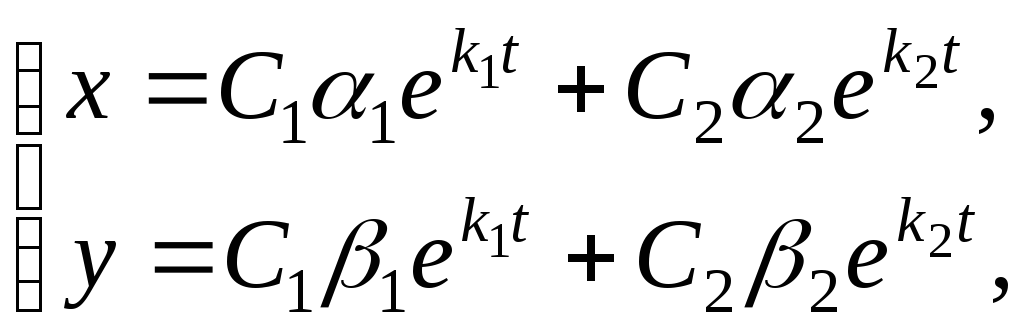
где
![]() – постоянные, определяемые из уравнений
(7) соответственно при
– постоянные, определяемые из уравнений
(7) соответственно при
![]() и при
и при
![]() ,
а
,
а
![]() – произвольные постоянные.
– произвольные постоянные.
При этом возможны следующие случаи.
-
Если
 ,
то точка покоя
,
то точка покоя
 асимптотически устойчива, т.к. из-за
множителей
асимптотически устойчива, т.к. из-за
множителей
 и
и
 в (8) все точки, находящиеся в начальный
момент
в (8) все точки, находящиеся в начальный
момент
 в любой
в любой
 - окрестности начала координат при
достаточно большом
- окрестности начала координат при
достаточно большом
 переходят в точки,
переходят в точки,  достаточно
большом переходят в точки, лежащие в
сколь угодно малой
достаточно
большом переходят в точки, лежащие в
сколь угодно малой
 – окрестности начала координат, а при
– окрестности начала координат, а при
 стремятся к началу координат. Точка
покоя рассматриваемого типа называется
устойчивым узлом.
стремятся к началу координат. Точка
покоя рассматриваемого типа называется
устойчивым узлом. -
Пусть
 и
и
 .
Этот случай переходит в предыдущий при
замене
.
Этот случай переходит в предыдущий при
замене
 на
на
 . Следовательно, траектории имеют такой
же вид, как и в предыдущем случае, но
только точки по траекториям движутся
в противоположном направлении. Очевидно,
что с возрастанием
. Следовательно, траектории имеют такой
же вид, как и в предыдущем случае, но
только точки по траекториям движутся
в противоположном направлении. Очевидно,
что с возрастанием
 точки, сколь угодно близкие к началу
координат, удаляются из
точки, сколь угодно близкие к началу
координат, удаляются из
 –окрестности начала координат – точка
покоя неустойчива в смысле Ляпунова.
Такая точка покоя называется неустойчивым
узлом.
–окрестности начала координат – точка
покоя неустойчива в смысле Ляпунова.
Такая точка покоя называется неустойчивым
узлом.
3. Если
![]() ,
то точка покоя тоже неустойчива, т.к.
движущаяся по траектории
,
то точка покоя тоже неустойчива, т.к.
движущаяся по траектории
![]() (9)
(9)
точка при
сколь угодно малых значениях
![]() с возрастанием
с возрастанием
![]() выходит из
выходит из
![]() – окрестности начала координат.
– окрестности начала координат.
В рассматриваемом случае существуют
движения, приближающиеся к началу
координат, а именно
рассматриваемом случае существуют
движения, приближающиеся к началу
координат, а именно
![]() .
.
При различных значениях
![]() получаем различные движения по одной
и той же прямой
получаем различные движения по одной
и той же прямой
![]() .
При возрастании
.
При возрастании
![]() точки на этой прямой движутся по
направлению к началу координат. Точки
траектории (9) движутся с возрастанием
точки на этой прямой движутся по
направлению к началу координат. Точки
траектории (9) движутся с возрастанием
![]() по прямой
по прямой
![]() ,
удаляясь от начала координат. Если же
,
удаляясь от начала координат. Если же
![]() и
и
![]() ,
то как при
,
то как при
![]() ,
так и при
,
так и при
![]() траектория покидает окрестность точки
покоя. Точка покоя рассматриваемого
типа называется седлом, т.к. траектория
в окрестности такой точки напоминают
линии уровня в окрестности седловой
точки поверхности
траектория покидает окрестность точки
покоя. Точка покоя рассматриваемого
типа называется седлом, т.к. траектория
в окрестности такой точки напоминают
линии уровня в окрестности седловой
точки поверхности
![]() .
.
б) Корни характеристического уравнения комплексные.
![]()
Общее решение системы (6) в этом случае можно представить в виде
 (10)
(10)
где
![]() – произвольные постоянные, а
– произвольные постоянные, а
![]() – некоторые линейные комбинации
– некоторые линейные комбинации
![]() и
и
![]() .
При этом возможны 3 случая:
.
При этом возможны 3 случая:
1)
![]()
Множитель
![]() ,
а второй - периодический множитель в
соотношении (10) – ограничен. При
,
а второй - периодический множитель в
соотношении (10) – ограничен. При
![]() траектории в силу периодичности вторых
множителей в (10) были бы замкнутыми
кривыми, окружающими точку покоя
траектории в силу периодичности вторых
множителей в (10) были бы замкнутыми
кривыми, окружающими точку покоя
![]() .
Из-за наличия множителя
.
Из-за наличия множителя
![]() при
при
![]() замкнутые кривые превращ
замкнутые кривые превращ
 аются
в спирали (направление закручивания
траекторий определяется по вектору
скорости
аются
в спирали (направление закручивания
траекторий определяется по вектору
скорости
![]() в какой-либо точке
в какой-либо точке
![]() ),
асимптотически приближающиеся при
),
асимптотически приближающиеся при
![]() к началу координат, причем при достаточно
большом
к началу координат, причем при достаточно
большом
![]() точки, находившиеся при
точки, находившиеся при
![]() в любой
в любой
![]() - окрестности начала координат, попадают
в заданную
- окрестности начала координат, попадают
в заданную
![]() – окрестность точки покоя
– окрестность точки покоя
![]() ,
а при дальнейшем увеличении
,
а при дальнейшем увеличении
![]() стремится к точке покоя. Следовательно,
точка покоя асимптотически устойчива
– это устойчивый фокус. Фокус
отличается от узла тем, что касательная
к траектории не стремится к определенному
пределу при приближении точки касания
к точке покоя.
стремится к точке покоя. Следовательно,
точка покоя асимптотически устойчива
– это устойчивый фокус. Фокус
отличается от узла тем, что касательная
к траектории не стремится к определенному
пределу при приближении точки касания
к точке покоя.
2)
![]()
Этот случай
переходит в предыдущий при замене
![]() на
на
![]() .
Следовательно, траектории имеют тот же
вид, что и в предыдущем случае, но движение
по ним при возрастании
.
Следовательно, траектории имеют тот же
вид, что и в предыдущем случае, но движение
по ним при возрастании
![]() происходит в противоположном направлении
(стрелки - от центра). Из-за наличия
возрастающего множителя
происходит в противоположном направлении
(стрелки - от центра). Из-за наличия
возрастающего множителя
![]() точки, находившиеся в начальный момент
сколь угодно близко к началу координат,
с возрастанием
точки, находившиеся в начальный момент
сколь угодно близко к началу координат,
с возрастанием
![]() удаляются из окрестности начала
координат. Точка покоя неустойчива –
это неустойчивый фокус.
удаляются из окрестности начала
координат. Точка покоя неустойчива –
это неустойчивый фокус.
3)
![]()
В этом случае
траекториями являются, как отмечалось
в пункте б)1), замкнутые кривые, содержащие
внутри себя точку покоя, называемую в
этом случае центром. Центр является
устойчивой точкой покоя. Т.к. для данной
![]() можно подобрать
можно подобрать
![]() такое, что замкнутые траектории, начальные
точки которых лежат в
такое, что замкнутые траектории, начальные
точки которых лежат в
![]() – окрестности начала координат, не
выходят за пределы
– окрестности начала координат, не
выходят за пределы
![]() – окрестности начала координат или,
что то же самое, можно подобрать столь
малые
– окрестности начала координат или,
что то же самое, можно подобрать столь
малые
![]() и
и
![]() ,
что решения
,
что решения
 (11)
(11)
будут удовлетворять неравенству
![]() .
.
Однако
асимптотической устойчивости в
рассматриваемом случае нет, т.к.
![]() и
и
![]() в (11) не стремятся к нулю при
в (11) не стремятся к нулю при
![]() .
.
в) Корни
кратные
![]() .
.
1)
![]() .
.
Общее решение имеет вид

причем может
быть
![]() ,
но тогда
,
но тогда
![]() и
и
![]() будут произвольными постоянными, чтобы
удовлетворить произвольным начальным
условиям.
будут произвольными постоянными, чтобы
удовлетворить произвольным начальным
условиям.
Из-за наличия
множителя
![]() при
при
![]() произведение
произведение
![]()
![]() стремятся
к нулю при
стремятся
к нулю при
![]() ,
,
причем при
достаточно большом
![]() все точки любой
все точки любой
![]() – окрестности начала координат попадают
в заданную
– окрестности начала координат попадают
в заданную
![]() – окрестность начала
– окрестность начала
к
 оординат
и, следовательно, точка покоя, асимптотически
устойчива. Точка покоя рассматриваемого
типа так же, как и в случае а)1) называется
вырожденным устойчивым узлом. Этот
узел занимает промежуточное положение
между узлом а)1) и фокусом б)1), т.к. при
сколь угодно малом изменении действительных
коэффициентов
оординат
и, следовательно, точка покоя, асимптотически
устойчива. Точка покоя рассматриваемого
типа так же, как и в случае а)1) называется
вырожденным устойчивым узлом. Этот
узел занимает промежуточное положение
между узлом а)1) и фокусом б)1), т.к. при
сколь угодно малом изменении действительных
коэффициентов
![]() он может превратится как в устойчивый
фокус, так и в устойчивый узел типа а)1),
ибо при сколь угодно малом изменении
коэффициентов кратный корень может
перейти как в пару комплексно сопряженных
корней, так и в пару действительных
различных корней. Если
он может превратится как в устойчивый
фокус, так и в устойчивый узел типа а)1),
ибо при сколь угодно малом изменении
коэффициентов кратный корень может
перейти как в пару комплексно сопряженных
корней, так и в пару действительных
различных корней. Если
![]() ,
то тоже получается устойчивый узел -
дикритический узел.
,
то тоже получается устойчивый узел -
дикритический узел.
-
Если
 ,
то замена
,
то замена
 на
на
 приводит к предыдущему cлучаю, т.е. вид
траекторий тот же, но движение происходит
в противоположном направлении. В этом
случае точка покоя, так же, как и в случае
а)2) – неустойчивый узел.
приводит к предыдущему cлучаю, т.е. вид
траекторий тот же, но движение происходит
в противоположном направлении. В этом
случае точка покоя, так же, как и в случае
а)2) – неустойчивый узел.
Таким образом,
исчерпаны все возможности, возникающие
в случае
![]() ,
т.к. при этом характеристическое уравнение
,
т.к. при этом характеристическое уравнение
![]()
не имеет
корней
![]() .
.
