
- •Федеральное агентство связи
- •Московский технический университет связи и информатики
- •Конспект лекций по обыкновенным дифференциальным уравнениям. Ч.3.
- •1. Понятие об устойчивости решений дифференциальных уравнений.
- •1.1. Простейшие типы точек покоя.
- •1.2. Замечания по поводу классификации точек покоя.
- •1.3. Однородная система линейных уравнений с постоянными коэффициентами.
- •2. Теоремы Ляпунова об устойчивости.
- •3. Исследование на устойчивость по первому приближению.
- •4. Дифференциальные уравнения с частными производными первого порядка
- •4.1. Первые интегралы систем дифференциальных уравнений
- •4.2. Характеристики
- •5. Линейные однородные дифференциальные уравнения в частных производных первого порядка с независимыми переменными.
- •6. Дифференциальные уравнения, допускающие понижение порядка.
- •Конспект лекций по обыкновенным дифференциальным уравнениям. Ч.3.
4. Дифференциальные уравнения с частными производными первого порядка
Наиболее
общее уравнение с частными производными
I
порядка с
![]() независимыми переменными может быть
записано в виде
независимыми переменными может быть
записано в виде
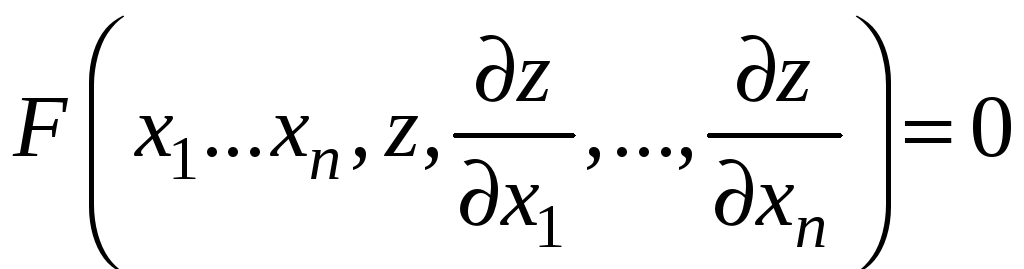 ,
(1)
,
(1)
где
![]() – заданная функция,
– заданная функция,
![]() - искомая функция,
- искомая функция,
![]() – независимые переменные.
– независимые переменные.
Пример 1.
![]() .
.
Интегрируя, имеем
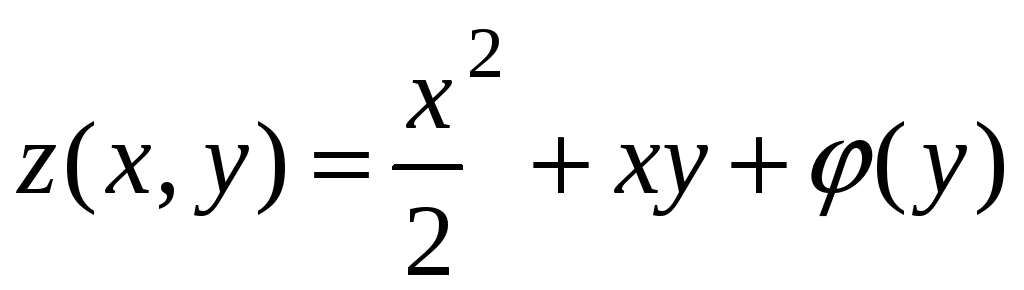 ,
,
где
![]() - произвольная функция от
- произвольная функция от
![]() .
.
Пример 2.
![]() .
.
Интегрируя
по
![]() ,
получим
,
получим
![]() ,
,
где
![]() - произвольная функция
- произвольная функция
![]() .
Интегрируем теперь по
.
Интегрируем теперь по
![]() :
:
![]() ,
,
где
![]() - произвольная функция от
- произвольная функция от
![]() .
Окончательно имеем:
.
Окончательно имеем:
![]() ,
,
где
![]() -
-
произвольная функция.
Из приведенных примеров видно, что общее решение дифференциального уравнения с частными производными I порядка зависит от одной произвольной функции, общее решение уравнения II порядка – от двух произвольных функций.
Линейным неоднородным уравнением или квазилинейным уравнением I порядка в частных производных называется уравнение вида:
![]() .
(2)
.
(2)
Это
уравнение линейно относительно
производных, но может быть нелинейным
относительно неизвестной функции
![]() .
.
Если
![]() ,
а коэффициенты
,
а коэффициенты
![]() не зависят от
не зависят от
![]() ,
то уравнение (2) называется линейным
однородным.
,
то уравнение (2) называется линейным
однородным.
Рассмотрим вначале квазилинейное уравнение с двумя независимыми переменными
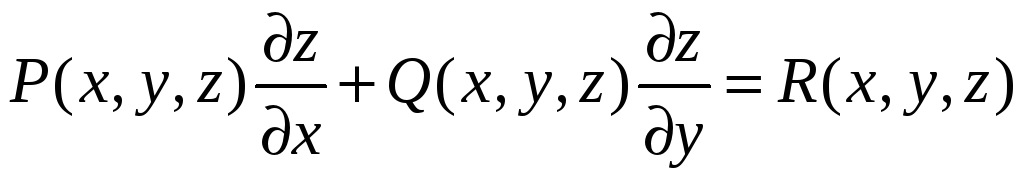 ,
(3)
,
(3)
где
![]() непрерывны в некоторой области изменения
переменных и не обращаются в нуль
одновременно.
непрерывны в некоторой области изменения
переменных и не обращаются в нуль
одновременно.
Рассмотрим непрерывное векторное поле
![]() .
.
Векторные линии этого
поля (т.е. линии, касательные к которым
в каждой точке имеют направление,
совпадающее с направлением вектора
![]() в той же точке) определяются из условия
коллинеарности вектора
в той же точке) определяются из условия
коллинеарности вектора
![]() ,
направленного по касательной к искомым
линиям, и вектора поля
,
направленного по касательной к искомым
линиям, и вектора поля
![]() :
:
![]()
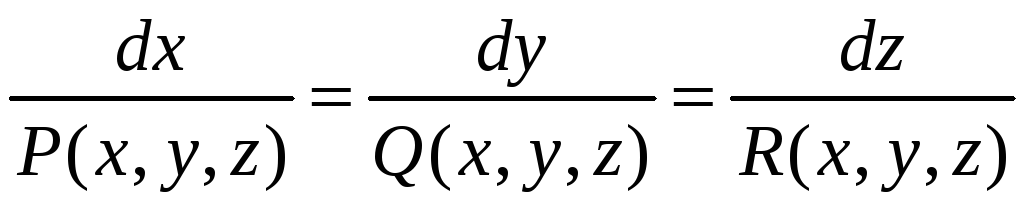 .
(4)
.
(4)
Это система дифференциальных уравнений векторных линий.
Поверхности, составленные из векторных линий, точнее, поверхности целиком содержащие векторные линии, имеющие хотя бы одну общую точку с поверхностью, называются векторными поверхностями.
Очевидно, векторные
поверхности можно получить, рассматривая
множество точек, лежащих на произвольно
выбранном непрерывно зависящем от
параметра однопараметрическом семействе
векторных линий. Векторная поверхность
характеризуется тем, что вектор
![]() ,
направленный по нормали к поверхности
в любой ее точке, ортогонален вектору
поля
,
направленный по нормали к поверхности
в любой ее точке, ортогонален вектору
поля
![]() :
:
![]() (5)
(5)
Если
векторная поверхность задана уравнением
![]() ,
то вектор
,
то вектор
![]() ,
,
и условие (5) принимает вид:
![]() .
(3)
.
(3)
Если
же векторная поверхность задана
уравнением
![]() (неявно), т.е.
(неявно), т.е.
![]() ,
,
то условие (5) имеет следующий вид:
![]() .
(6)
.
(6)
Следовательно, для нахождения векторных поверхностей надо проинтегрировать квазилинейное уравнение (3) или линейное однородное уравнение (6) в зависимости от того, ищем ли мы уравнение искомых векторных поверхностей в явном или неявном виде.
Т.к. векторные поверхности могут быть составлены из векторных линий, то интегрирование уравнений (3) или (6) сводится к интегрированию системы обыкновенных дифференциальных уравнений векторных линий (4).
4.1. Первые интегралы систем дифференциальных уравнений
Рассмотрим систему дифференциальных уравнений
![]() .
(7)
.
(7)
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием системы (7), но уже легко интегрирующееся, например, являющееся уравнением вида
![]() )
)
или уравнением, которое может быть сведено путем замены переменных к какому-нибудь интегрируемому типу уравнений с одной неизвестной функцией.
Пример 3.
![]() .
.
Складывая обе части равенств, найдем интегрируемую комбинацию
![]() ,
,
т.е.
 ,
,
откуда
![]() .
.
Вычитая, найдем вторую интегрируемую комбинацию
![]() ,
,
откуда
![]() .
.
Итак,
![]() ,
,
![]() .
.
Следовательно,
![]()
![]() .
.
Одна интегрируемая комбинация дает возможность получить одно соотношение
![]() ,
,
связывающее неизвестные функции и независимую переменную; такое соотношение называется первым интегралом системы (7).
Итак, первым интегралом
![]() (8)
(8)
системы уравнений (7) называется соотношение, не равное тождественно постоянной, содержащее в левой части независимую переменную и искомые функции и принимающее постоянное значение, если вместо искомых функций подставить какое-нибудь решение системы (7).
Геометрически
первый интеграл (8) при фиксированном
![]() можно интерпретировать как
можно интерпретировать как
![]() -мерную
поверхность в
-мерную
поверхность в
![]() -мерном пространстве с координатами
-мерном пространстве с координатами
![]() ,
обладающую тем свойством, что каждая
интегральная кривая, имеющая общую
точку с этой поверхностью, целиком лежит
на поверхности.
,
обладающую тем свойством, что каждая
интегральная кривая, имеющая общую
точку с этой поверхностью, целиком лежит
на поверхности.
При
переменном
![]() получаем семейство непересекающихся
поверхностей, состоящих из точек
некоторого
получаем семейство непересекающихся
поверхностей, состоящих из точек
некоторого
![]() -
параметрического семейства интегральных
кривых системы (7).
-
параметрического семейства интегральных
кривых системы (7).
Если
найдено
![]() интегрируемых комбинаций, то получаем
интегрируемых комбинаций, то получаем
![]() первых интегралов
первых интегралов
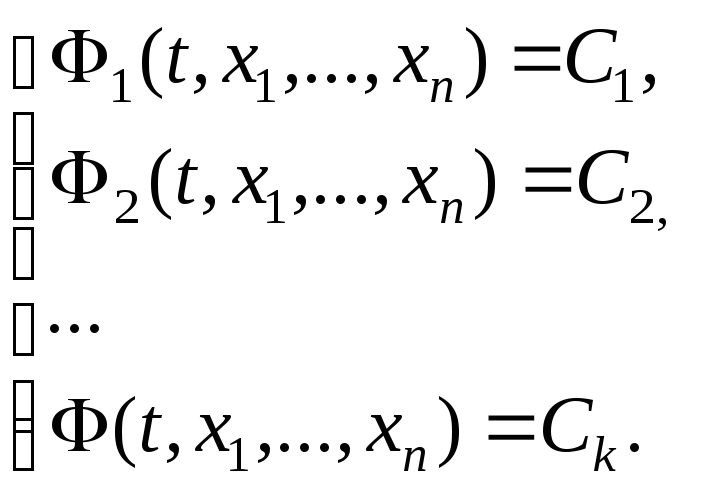 (9)
(9)
Если все эти интегралы независимы, то есть если хотя бы один из определителей
![]() ,
,
где
![]() какие-нибудь
какие-нибудь
![]() функций из
функций из
![]() ,
не равен нулю, то из системы (9) можно
выразить
,
не равен нулю, то из системы (9) можно
выразить
![]() неизвестных функций через остальные
и, подставив в систему (7), понизить ее
размер. Если
неизвестных функций через остальные
и, подставив в систему (7), понизить ее
размер. Если
![]() и все интегралы независимы, то все
неизвестные функции определяются из
(9).
и все интегралы независимы, то все
неизвестные функции определяются из
(9).
Пример 4.

где
![]() .
Умножив первое уравнение на
.
Умножив первое уравнение на
![]() ,
второе – на
,
второе – на
![]() ,
третье – на
,
третье – на
![]() и складывая,
получим
и складывая,
получим
![]() ,
,
т.е. имеем I- й интеграл:
![]() .
.
Умножим
первое уравнение на
![]() ,
второе – на
,
второе – на
![]() ,
третье – на
,
третье – на
![]() и складывая, имеем
и складывая, имеем
![]() .
.
Откуда получаем следующий I- й интеграл:
![]() .
.
За
исключением случая
![]() ,
когда система интегрируется непосредственно,
найденные первые интегралы независимы
и, следовательно, можно исключить две
неизвестные функции, а для нахождения
третьей получим одно уравнение с
разделяющимися переменными.
,
когда система интегрируется непосредственно,
найденные первые интегралы независимы
и, следовательно, можно исключить две
неизвестные функции, а для нахождения
третьей получим одно уравнение с
разделяющимися переменными.
Для нахождения интегрируемых комбинаций часто удобно переходить к так называемой симметричной форме записи системы уравнений (7):
![]() , (10)
, (10)
где
![]() =
=![]() .
.
